13.1.2. Математическое ожидание

Определение 5. Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятности этих значений.

Замечание 2. Если дискретная случайная величина задана конечным рядом распределения, то математическое ожидание вычисляется по формуле: .

Замечание 3. Если дискретная случайная величина задана бесконечным рядом распределения, то если ряд сходится абсолютно, то его сумма называется математическим ожиданием дискретной случайной величины Х.

Замечание 3. Математическое ожидание меньше наибольшего и больше наименьшего значений случайной величины. В этом смысле оно расположение распределения случайной величины. Иногда его называют центром распределения.

Свойства математического ожидания дискретной случайной величины

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: .

Доказательство. Постоянную С можно рассматривать как дискретную случайную величину, принимающую одно возможное значение С с вероятностью 1. Следовательно, .

Определение 6. Произведением постоянной величины С на случайную величину Х называется случайная величина СХ, возможные значения которой равны произведениям постоянной С на возможные значения Х; вероятность возможных значений СХ равны вероятностям соответствующих значений Х.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: .

Доказательство (для ДСВ). Поострить ряд распределения Х и СХ. По определению составить математическое ожидание СХ.

Определение 7. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Определение 8. Несколько случайных величин называются взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные случайные величины.

Определение 9. Произведением независимых случайных величин Х и У называется случайная величина ХУ, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение У; вероятности возможных значений произведения ХУ равны произведениям вероятностей возможных значений сомножителей.

Пример.

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: .

Доказательство (для ДСВ). Выписать ряды распределения Х, У и ХУ. Составить , перегруппировать.

Следствие. Математическое ожидание произведения нескольких (конечного числа) независимых случайных величин равно произведению их математических ожиданий: .

Определение 10. Суммой случайных величин Х и У называется случайная величина Х+У, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением У; вероятности возможных значений Х+У для независимых случайных величин равны произведениям вероятностей слагаемых, для зависимых – произведениям вероятности одного слагаемого на условную вероятность другого.

Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: .

Доказательство (для ДСВ). Выписать ряды распределения Х, У и ХУ. Составить , перегруппировать относительно возможных значений, вынести общий множитель, учесть, что сумма вероятностей случайной величины равна 1.

Следствие 1. Математическое ожидание суммы нескольких (конечного числа) случайных величин равно сумме их математических ожиданий: .

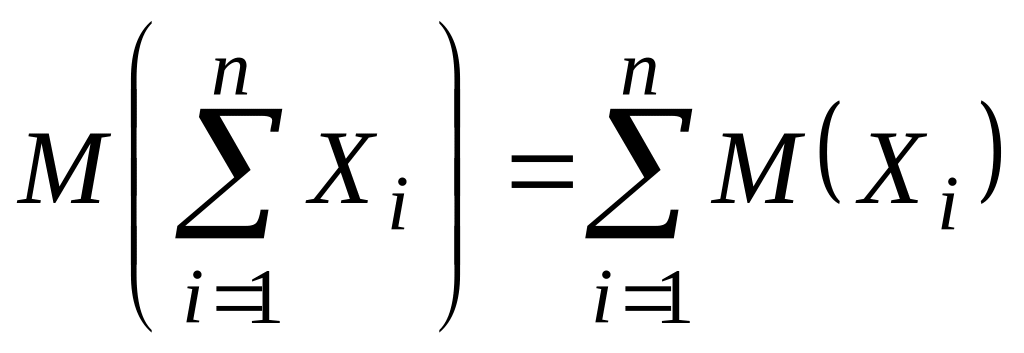Следствие 2. .

Следствие 3. .