12. Уравнение Шредингера для электрона в атоме, квантовые числа

Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия Не⁺, двукратно ионизованного литияLi⁺⁺ и др.) сводится к задаче о движении электрона в кулоновском поле ядра.

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),

                                                       (223.1)

где r — расстояние между электроном и ядром. Графически функция U(r) изображена жирной кривой на рис. 302. U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает.

Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера (217.5), учитывающему значение (223.1):

                                                 (223.2)

где т — масса электрона, Е — полная энергия электрона в атоме. Так как поле, в котором движется электрон, является центрально-симметричным, то для решения уравнения (223.2) обычно используют сферическую систему координат: r, q, j. Не вдаваясь в математическое решение этой задачи, ограничимся рассмотрением важнейших результатов, которые из него следуют, пояснив их физический смысл.

Квантовые числа — энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.

1. Главное квaнтовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n = 1, 2, 3, . . .)

2. Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 доn-1 (l = 0, 1, 2, 3,..., n-1). Каждому значению l соответствует орбиталь особой формы. Орбитали с l = 0 называются s-орбиталями,  l = 1 – р-орбиталями (3 типа, отличающихся магнитным квантовым числом m),  l = 2 – d-орбиталями (5 типов),  l = 3 – f-орбиталями (7 типов).

3. Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от +l до -l, включая 0. Например, при l = 1 число m принимает 3 значения: +1, 0, -1, поэтому существуют 3 типа  р-АО:  р_x,  р_y,  р_z.

4. Спиновое квантовое число s может принимать лишь два возможных значения +1/2 и -1/2. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона, называемого спином (от англ. веретено). Для обозначения электронов с различными спинами используются символы: 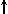  и  .

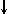13. Спектры излучения атомов, правила отпора

Излучение оптических спектров показало, что сложные вещества (состоящие из разных атомов) при нагреве испускают электромагнитные волны всех длин в видимом диапазоне (Например: солнце, лампы накаливания). Однако чистые вещества, многоатомные, имеют спектры испускания, состоящие из отдельных длин волн.

Эмпирически (путём подбора чисел) было установлено, что длины волн в видимой части электромагнитных волн для водородного газа определялись λ = λ₀n² / (n² - 4), где n - целое число, которое отсчитывается от цифры 3. Так как ν = c/λ или λ = c/ν, то подставив это в эмпирическую формулу, получим ν = ν₀*(n² - 4) / n² = ν₀*(1 - 4/n²) = 4ν₀*(1/2² - 1/n²).  – это формула, впервые найденная Бальмером для определения частоты испускания электромагнитного излучения атомарным водородом.

Спектр излучения атомарного водорода состоит из отдельных спектральных линий, расположенных в определенном порядке. Спектральные линии образуют серии, линии которых могут быть представлены в виде обобщенной (сериальной) формулы Бальмера: где m и n – номера состояний, R – постоянная Ридберга. При заданном m число n принимает все целочисленные значения, начиная с m+1.

m = 1 – серия Лаймана (для ультрафиолетовой области);

m = 2 – серия Бальмера;

m = 3 – серия Пашена;

m = 4 – серия Брэкета;

m = 5 – серия Пфунда.

Если в обобщенной формуле Бальмера n>m, то спектр испускания; если m>n, то спектр поглощения. Таким образом, эмпирически ещё до введения теорий Планка и Эйнштейна анализ спектров излучения чистых веществ, проведённый Бальмером, предвосхитил осмысление положения об электромагнитном излучении как о потоке дискретных порций энергии, не отрицая в то же время проявления волновых свойств электромагнитного излучения.

Правилами отбора в спектроскопии называют ограничения и запрет на переходы между уровнями квантомеханической системы с поглощением или излучением фотона, наложенные законами сохранения и симметрией.

Гармонический осциллятор

Разрешенные переходы гармонического осциллятора удовлетворяют правилу отбора:

,

где n_f и n_i — квантовые числа конечного и начального состояния соответственно. То есть, переходы могут происходить только между соседними состояниями. Учитывая то, что состояния гармонического осциллятора эквидистантны, это приводит к существованию в спектре излучения или поглощения единой линии.

Магнитное квантовое число

Для магнитного квантового числа

 .

Свет, который испускается при переходе с  , линейно поляризован. При переходах с   испускается циркулярно поляризованный свет.

Квантовое число полного момента 

Для квантового числа полного момента многоэлектронной системы

 .

Кроме того, запрещены переходы между состояниями, в которых оба квантовых числа полного момента равны нулю.

Орбитальное квантовое число

Для орбитального квантового числа

 .