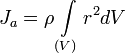Kollokvium_Teoria
.docx|
Вопрос № 4 Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. Величина инертности характеризуется массой тела. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Второй закон Ньютона. В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
где Или в более известном виде:
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.
где
где
Когда на тело действуют несколько сил, с учётом принципа суперпозиции второй закон Ньютона записывается:
или
Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. Для скоростей, приближенных к скорости света, используются законы теории относительности. Третий закон Ньютона. Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Закон отражает принцип парного взаимодействия. То есть все силы в природе рождаются парами.
Вопрос № 5 Сила упругости, трения, однородная тяжести, гравитационная. Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации. В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности. Вектор силы противоположен направлению деформации тела (смещению его молекул).
Закон Гука. В простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид:
где В словесной формулировке закон Гука звучит следующим образом: Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации. Сила трения При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на: Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения. Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого. Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения. Основная формула: F=M*N, где M-коэффициент трения, N-сила реакции опоры. Сила тяжести Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести.По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести Fт=GMm/R2 где М - масса Земли; R - радиус Земли. Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле (2,28) модуль ускорения свободного падения g находят по формуле g=Fт/m=GM/R2.
Из формулы (2.29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде Fт=mg
В 1687 г. Ньютон установил один из фундаментальных законов механики, получивший название закона всемирного тяготения: любые две материальные частицы притягиваются друг к другу с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Эту силу называют силой тяготения (или гравитационной силой).
Формула закона всемирного тяготения для материальных точек Если взаимодействующие между собой тела можно считать материальными точками или же если они имеют правильную сферическую форму, то формула закона всемирного тяготения имеет вид F=Gm1m2/r2 (2.26) где F - модуль силы тяготения; m1 и m2 - массы материальных точек; r - расстояние между ними; G - коэффициент пропорциональности, называемый постоянной всемирного тяготения или гравитационной постоянной. Силы, с которыми взаимно притягиваются тела по закону всемирного тяготения, являются центральными, т. е. они направлены вдоль прямой, соединяющей центры взаимодействующих тел. Гравитационная постоянная Из (2.26) при m1=m2=m имеем G=Fr2/m2. Из этой формулы видно, что гравитационная постоянная численно равна силе взаимного тяготения двух материальных точек, имеющих массы, равные единице массы, и находящихся друг от друга на расстоянии, равном единице длины. Числовое значение гравитационной постоянной устанавливают экспериментально. Впервые это сделал английский ученый Кэвендиш с помощью крутильного динамометра (крутильных весов). В СИ гравитационная постоянная имеет значение G = 6,67·10-11 Нм2/кг2. Следовательно, две материальные точки массой 1 кг каждая, находящиеся друг от друга на расстоянии 1 м, взаимно притягиваются гравитационной силой, равной 6,67·10-11 Н. Вопрос № 6 Вес тела. Сила, с которой тело, находящееся под действием силы тяжести, действует на подставку или подвес, называется весом тела. В частности, если тело подвешено к динамометру, то оно действует на динамометр с силой своего веса. По третьему закону Ньютона динамометр действует на тело с такой же силой. Если при этом динамометр и подвешенное к нему тело покоятся относительно Земли, то, значит, сумма сил, действующих на тело, равна нулю, так что вес тела равен силе притяжения тела Землей. Таким образом, подвешивая тело к динамометру, мы можем определить вес тела и равную ему силу притяжения тела Землей. Поэтому динамометры нередко называют пружинными весами. Сила веса возникает в результате притяжения Земли, но по величине может отличаться от силы притяжения Земли. Прежде всего, это может быть в тех случаях, когда кроме Земли и подвеса на данное тело действуют какие-либо другие тела. Так, если тело, подвешенное к весам, погружено в воду, то оно будет действовать на подвес со значительно меньшей силой, чем сила притяжения Земли. Эти случаи будут рассмотрены позднее (см. далее, гл. VII), а сейчас рассмотрим, почему необходимо, как только что было оговорено, чтобы весы и взвешиваемое тело покоились относительно Земли. Вопрос № 7 Работа, мощность. Рабо́та силы мера действия силы, зависящая от численной величины и направления силы F и от перемещения s точки её приложения. Если сила F численно и по направлению постоянная, а перемещение прямолинейно, то работа А = F·s cosα, где α — угол между направлениями силы и перемещения. Работа силы (сил) над одной точкой Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше в этом параграфе будем говорить об одной силе.
При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]:
Здесь
точкой обозначено скалярное
произведение[4], Если сила не постоянна, то в этом случае она вычисляется как интеграл
(подразумевается
суммирование по кривой, которая
является пределом ломаной, составленной
из последовательных перемещений Если существует зависимость силы от координат, интеграл определяется следующим образом:
где Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю. Работа силы (сил) над системой или неточечным телом Работа сил над системой материальных точек определяется как сумма работ этих сил над каждой точкой (работы, совершённые над каждой точкой системы, суммируются в суммарную работу этих сил над системой. Даже если изначально тело не является системой дискретных точек, можно разбить его (мысленно) на множество бесконечно малых элементов (кусочков), каждый из которых считать материальной точкой, вычисляя работу в соответствии с определением выше. В этом случае дискретная сумма заменяется на интеграл. Эти определения могут быть использованы как для какой-то конкретной силы или класса сил — для вычисления именно их работы отдельно, так и для вычисления полной работы, совершаемой всеми силами, действующими на систему. Мощность Мощность, физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена. Если работа производится равномерно, то М. определяется формулой N = A/t, где А — работа, произведённая за время t; в общем случае N = dA/dt; где dA — элементарная работа, производимая за элементарный промежуток времени dt (обычно 1 сек). М. измеряется в ваттах, а в технике иногда в лошадиных силах.
Вопрос № 12 ЦЕНТР МАСС (центр инерции) тела (системы материальных точек) - точка, характеризующая распределение масс в теле или механическлй системе. При движении тела его центр масс движется как материальная точка с массой, равной массе всего тела, к которой приложены все силы, действующие на это тело. Понятие центра масс отличается от понятия о центре тяжести тем, что последнее имеет смысл только для твердого тела, находящегося в однородном поле тяжести. Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:
где
— масса i-й точки. Описание свойств. Возьмем тело, в котором сила тяжести действует на каждую из составляющих его частей, a mi — масса одной из этих частей. Действующая на нее сила тяжести будет тогда равна произведению mi на g. Возникает вопрос: в какой точке нужно приложить одну-единственную силу, чтобы сбалансировать притяжение всего тела так, чтобы оно (если это твердое тело) не вращалось? Ответ: сила должна проходить через центр масс. Доказывается это следующим образом. Чтобы тело не вращалось, сумма моментов всех сил должна быть равна нулю, ибо если нет момента сил, то нет и изменения момента количества движения, а поэтому нет и вращения. Таким образом, мы должны подсчитать сумму всех моментов, действующих на все частицы, и посмотреть, какой получится полный момент относительно любой данной оси: он должен быть равен нулю, если ось проходит через центр масс. Направив ось х горизонтально, а ось у вертикально, мы найдем, что моменты сил равны силам, направленным вниз, умноженным на плечо х (т. е. сила на плечо относительно той оси, для которой измеряется момент силы). Полный же момент равен сумме
Чтобы полный момент отсутствовал, сумма Σmixi должна быть равна нулю. Но эта сумма равна MX — полной массе, умноженной на расстояние от оси х до центра масс. Итак, это расстояние должно быть равно нулю. Разумеется, мы провели проверку только для x-направления, однако если мы действительно взяли центр масс, то тело должно быть уравновешено в любом положении, поэтому, повернув его на 90°, мы вместо оси х получим ось у. Другими словами, если держать тело за центр масс, то параллельное гравитационное поле не дает никакого момента сил. Если же объект настолько велик, что становится существенной непараллельность сил притяжения, то точку, в которой должна быть приложена уравновешивающая сила, описать не просто: она несколько отклоняется от центра масс. Вот почему нужно помнить, что центр масс и центр тяжести — разные вещи. Тот факт, что тело, поддерживаемое точно за центр масс, уравновешено в любом положении, имеет еще одно интересное следствие. Если вместо гравитационных сил взять инерционные псевдосилы, возникающие вследствие ускорения, то, чтобы найти точку, уцепившись за которую мы уравновесим все моменты этих сил, можно использовать ту же самую математическую процедуру. Предположим, что мы заключили тело внутрь ящика, который ускоряется вместе со всем его содержимым. Тогда, с точки зрения наблюдателя, сидящего в этом ящике, на тело вследствие инерции будет действовать некая эффективная сила. Иначе говоря, чтобы заставить тело двигаться вместе с ящиком, нужно подталкивать и ускорять его. Эта сила «уравновешивается силой инерции», которая равна массе тела, умноженной на ускорение ящика. Наблюдателю в ящике будет казаться, будто тело находится в однородном гравитационном поле, величина g которого равна ускорению ящика α. Таким образом, инерционные силы, возникающие вследствие ускорения тела, не имеют момента относительно центра масс. Этот факт имеет очень интересное следствие. В инерционной системе, движущейся без ускорения, момент сил всегда равен скорости изменения момента количества движения. Однако равенство момента силы и скорости изменения момента количества движения остается справедливым даже для ускоряющегося тела, если взять ось, проходящую через центр масс. Таким образом, теорема о равенстве момента сил скорости изменения момента количества движения верна в двух случаях; 1) ось фиксирована — в инерциальной системе; 2) ось проходит через центр масс — даже когда тело ускоряется. Вопрос № 13 Момент импульса частицы. Моментом импульса L частицы Aотносительно точки О называется величина, равная векторному произведению радиус-вектора частицы на ее импульс p: L = [r·p] = [r·mv]. (7.1) В общем случае произвольного движения относительно точки О модуль момента импульса частицы равен: L = r·m·v·sin() = R·m·v, где R - плечо импульса частицы относительно точки О
В общем случае произвольного движения относительно точки О модуль момента импульса частицы равен: L = r·m·v·sin() = R·m·v, где R - плечо импульса частицы относительно точки О Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где (В
пределе количество частиц может быть
бесконечным, например, в случае твердого
тела с непрерывно распределенной
массой или вообще распределенной
системы это может быть записано
как В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с. Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Момент силы частицы определяется как векторное произведение:
где Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой. Момент силы — производная по времени от момента импульса,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости. Уравнение моментов
скорость
изменения момента импульса частицы
относительно некоторой точки С помощью уравнения моментов решаются две задачи: 1.
Известно: 2.
Известно:
Закон сохранения момента импульса: в инерциальной системе отсчета момент импульса замкнутой системы частиц остается постоянным, т.е, не меняется со временем. Причем это справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Таким образом, в инерциальной системе отсчета момент импульса замкнутой системы частиц
Вопрос №14 Рассмотрим
абсолютно твердое тело, вращающееся
около неподвижной оси
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
Используя выражение (1), получаем:
где Кинетическая энергия при плоском движении. Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:
где
так
как Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений (теорема Кенига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения. Вопрос № 17 При
вращении твёрдого тела относительно
неподвижной оси, все точки тела движутся
по плоским круговым траекториям.
Выделим частицу mi тела, вращающегося
вокруг оси z (рис. 9.2). Положение
частицы зададим радиус-вектором Рис. 9.2 Рассматривая твёрдое тело как неизменную систему материальных точек, для каждой из них можно записать уравнение моментов: В левой части этого уравнения — момент внешних сил относительно оси z, действующий на частицу mi. Справа — производная по времени проекции момента импульса частицы на ту же ось. Момент импульса частицы относительно центра 0 (по определению) равен:
Заметим,
что для всех частиц Li = miriVi = miriwRi. Так
как Учитывая этот результат, перепишем уравнение (9.1) ещё раз: Подобные уравнения могут быть составлены для всех точек твёрдого тела. Просуммировав все эти уравнения, получим закон вращательного движения твёрдого тела:
или Здесь: Mz — суммарный момент всех внешних сил, вращающих твёрдое тело вокруг оси z; wz — угловая скорость вращения; Lz = Izwz — момент импульса тела относительно оси z. Если момент инерции твёрдого тела Iz не меняется, уравнению (9.4) можно придать такой вид: Здесь ε = Уравнение (9.5) называется основным уравнением динамики для твёрдого тела, вращающегося вокруг неподвижной оси. Вопрос №20 Преобразования Лоренца - преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Инерциальная система отсчёта – система отсчёта, движущаяся прямолинейно с постоянной скоростью v. Преобразования Лоренца отражают равноправие всех инерциальных систем отсчёта в описании законов природы. Если инерциальная система отсчёта K' движется относительно инерциальной системы отсчёта K с постоянной скоростью v вдоль оси x, то преобразования Лоренца имеют вид
c - скорость света в вакууме, β = v/c. Формулы, выражающие x', y', z', t' через x, y, z, t получаются из соотношения (1) заменой v на -v. c - скорость света в вакууме, β = v/c. Формулы, выражающие x', y', z', t' через x, y, z, t получаются из соотношения (1) заменой v на -v. При v << c преобразования Лоренца переходят в преобразования Галилея x = x' + vt, y = y', z = z', t = t'. Из преобразований Лоренца следует, что промежутки времени Δt и отрезки длины Δl зависят от движения системы отсчёта. Если в системе K' два события, происходящие в одном и том же месте, разделены интервалом времени Δt', то в системе K эти же происходящие в разных местах события разделены промежутком времени Δt
Если отрезок, покоящийся в системе K', имеет длину Δl', то его длина Δl в системе K, т.е. расстояние между двумя одновременными в K событиями регистрации положения концов отрезка, принимает значение
Поперечные размеры тел при этом не изменяются. Формулы преобразования скорости:
Электрическое поле E и магнитное поле H при преобразовании Лоренца преобразуются следующим образом:
Координаты 4-мерного вектора энергии-импульса с компонентами (ε/c, px, py, pz) при преобразовании Лоренца преобразуются следующим образом:
Энергия
частицы Импульс
частицы Преобразования Лоренца, указывающие на относительность промежутков времени и отрезков длины между двумя событиями, оставляют инвариантной, т.е. не зависящей от выбора системы отсчёта, их комбинацию, называемую интервалом.
Инвариантом при преобразовании Лоренца является также квадрат 4-вектора энергии-импульса
|
Вопрос № 1 Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел. Существуют инерциальные и неинерциальные системы отсчета. Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся. Неинерциа́льная систе́ма отсчёта — система отсчёта, не являющаяся инерциальной. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной. Идеализированная модель физического тела - в физике - абстрактный объект: - являющийся моделью реального объекта; и - обладающий некоторыми физическими свойствами реального объекта, существенными для определенного круга задач. Модели такого рода позволяют: - изучать реальные объекты; - формулировать физические законы; и - создавать физические теории. Перемещаясь из одной точки в другую, тело описывает некоторую линию, которую называют траекторией движения тела. Путь - длина участка траектории материальной точки, пройденного ею за определенное время. Перемещение определяется как вектор, который связывает начальную и конечную точки траектории движения тела. Описать движение тела – это значит указать способ определения его положения в пространстве в любой момент времени. 1. Векторный способ: В этом случае положение материальной точки задается с помощью радиус вектора, представляющий собой вектор, проведенный из точки О, соответствующей началу отсчета, в интересующую нас точку. В процессе движения материальной точки её радиус-вектор может меняться по модулю и направлению траектории точки. 2. Координатный способ. В этом случае положение материально точки на плоскости в произвольный момент времени определяется координатами X и Y, которые представляют собой проекции радиус вектора тела на оси. При движении тела координаты его изменяются во времени, являясь функциями (T): X(T) = X, Y(T) = Y, если эти функции известны, то они определяют положение тела в любой момент времени. Зная эти зависимости, можно найти положение тела, проекции на его скорость, модуль и направление a и V в любой момент времени. Вопрос № 2 Естественный способ, применяется, если траектория материальной точки известна заранее. На заданной траектории выбирают начало отсчёта - неподвижную точку, а положение материальной точки определяют при помощи дуговой координаты, представляющей собой расстояние вдоль траектории от выбранного начала отсчета до самой материальной точки. Вопрос № 3 Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
Количественные характеристики, раскрывающие форму и характер движений, называются кинематическими .
Они описывают движения в пространстве и во времени. Соответственно различают характеристики: - пространственные; - временные; - пространственно-временные. Пространственные характеристики позволяют определить, каково исходное и конечное положения при движении (координата), какова между ними разница, насколько они изменились (перемещение) и через какие промежуточные положения выполнялось движение (траектория), т.е. пространственные характеристики в целом определяют пространственную форму движений человека.
Угловые кинематические характеристики При вращении абсолютно твердого тела вокруг неподвижной оси все точки этого тела описывают окружности. Линейные скорости этих точек различны, а угловая скорость для всех точек одинакова, поэтому она характеризует в данном случае движение всего тела.
Рассматривая угловые кинематические характеристики, отнесем их к движению частицы по окружности. Пусть частица движется по окружности в плоскости XY, вращаясь вокруг оси Z ( рис. 1.5,а ). Положение частицы на окружности можно задать углом Dj радиуса-вектора r с осью Х. Чтобы с помощью элементарного угла Dj определить не только изменение положения, но и направление движения частицы, введем вектор DY, которому условно припишем направление, перпендикулярное плоскости, в которой лежит дуга DS так, чтобы направление движения и направление вектора DY были связаны как вращение рукоятки буравчика (с правой нарезкой) и поступательное движение буравчика (рис. 1.5,б). Определим далее угловую скорость и угловое ускорение. Угловой скоростью называется вектор w = Dj /dt (1.17)
Численно угловая скорость w равна углу поворота радиуса-вектора материальной точки в единицу времени (или углу поворота тела в единицу времени, если речь идет о вращении тела). Вектор угловой скорости направлен перпендикулярно плоскости, в которой лежит дуга, описываемая материальной точкой, или направлена вдоль оси вращения тела (рис. 1.6 а,б ).
Угловое ускорение (быстрота изменения угловой скорости) определяется уравнением e = dw/dt ( 1.18) Угловое ускорение можно выразить и как вторую производную угла поворота радиуса- вектора по времени. Будем обозначать угловое ускорение греческой буквой e. Направление углового ускорения совпадает с направлением угловой скорости, если движение ускоренное и противоположно, если движение замедленное. Угловые кинематические характеристики движения связаны с линейными достаточно простыми соотношениями. Найдем эту связь. Обратимся к рис. (1.7 а,б).
Точка движется по окружности радиуса R. Примем центр окружности за начало отсчета. Из чертежа ясно следующее : V = dS/dt = Rdj /dt = Rw (1.22) Вектор v перпендикулярен плоскости, в которой лежат R и w, угол между R и w равен 90 градусам. Следовательно, можно записать векторное равенство V = [wR] (1.23) a=dV/dt = d(wr)/dt = [dw/dt]r + [dr/dt]w (1.24) a = [er]+[ wV ] Первое слагаемое в правой части (1.24) представляет собой вектор, направленный по касательной к траектории точки, движущейся по окружности, и является, следовательно, тангенциальным ускорением at = [er] (1.25) Второе слагаемое в (1.24) - вектор, направленный по радиусу кривизны к центру траектории. Это нормальное ускорение an = [wV] (1.26) Если за начало отсчета выбран центр окружности, по которой движется точка, то модули ускорений определяются как at = eR; an = wV = w2R (1.27)
Вопрос № 9 Кинетическая энергия и ее связь с результирующей силой. Кинетическая
энергия определяется соотношением
Умножим обе части на ds.
Из
определения скорости известно, что
Заменяя
Из
этого выражения видно, что приращение
энергии - это есть работа. Также можно
заметить, что
Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии. Вопрос № 10 Собственная и внешняя потенциальная энергия системы материальных точек. Полная механическая энергия системы в поле внешних консервативных сил, ее связь с работой неконсервативных и сторонних сил. Закон сохранения полной механической энергии. Универсальный закон сохранения энергии.
а)
Определим понятие потенциальной
энергии. Пусть есть поле консервативных
сил. Значение силы в каждой точке этого
поля определяется некоторой функцией
координат
Поскольку работа в поле консервативных сил не зависит от пути, значения в каждой точке поля определяются однозначно. Такая
функция
б) Рассмотрим взаимодействие частиц внутри системы. Возьмем простейшую систему из двух материальных точек. Силы, с которыми они взаимодействуют, будем полагать направлены вдоль прямой, соединяющей обе частицы, и зависят от расстояния между частицами. Найдем работу внутренних сил.
dr1 – перемещение первой частицы dr2 – перемещение второй частицы
Выражение
В случае гравитационного взаимодействия:
Для
системы из N частиц, общая потенциальной
энергии взаимодействия система будет
равна сумме всех взаимодействий частиц
взятых попарно. Например для системы
из трех частиц
Примером потенциальной энергии внутреннего взаимодействии является пружина. При ее сжатии и растяжении изменяется именно эта энергия. в) Сумма кинетической и потенциальной энергий называется полной механической энергией частицы.
Кинетическая и потенциальная энергия могут переходить одна в другую. Однако, полная механическая энергия частицы, движущейся в поле консервативных сил, остаётся постоянной (закон сохр. полн. мех. эн.). Работа неконсервативных сил приводит к изменению общей энергии (потенциальной энергии внутреннего взаимодействия и/или кинетической энергии и/или потенциальной энергии). г) Универсальный закон сохранения энергии заключается в том, что полная энергия системы всегда остается постоянной. Энергия является неуничтожимой и может только переходить из одного вида в другой. В основе закона сохранения механической энергии лежит однородность времени, т.е. равнозначность всех моментов времени в разных системах координат (время абсолютно). Вопрос № 11 Импульс частицы
- это произведение ее массы на скорость Перейдем к более подробному рассмотрению импульса. Прежде всего, запишем основное уравнение ньютоновой динамики (3.6) в иной форме-через импульс:
т.
е. производная
импульса материальной точки по времени
равна действующей на нее силе.
В частности, если Заметим,
что в неинерциальной системе отсчета
результирующая сила Уравнение (4.1) позволяет
найти приращение импульса частицы за
любой промежуток времени, если известна
зависимость силы
Если
сила Пример.
На частицу, которая в начальный
момент Перейдем к рассмотрению более сложного случая. Рассмотрим произвольную систему частиц. Введем понятие импульса системы как векторной суммы импульсов ее отдельных частиц:
где Найдем физическую величину, которая определяет изменение импульса системы. Для этого продифференцируем соотношение (4.3) по времени:
Согласно (4.1),
где
В этом равенстве двойная сумма справа - это сумма всех внутренних сил. В соответствии с третьим законом Ньютона силы взаимодействия между частицами системы попарно одинаковы по модулю и противоположны по направлению. Поэтому результирующая сила в каждой паре взаимодействия равна нулю, а значит, равна нулю и векторная сумма всех внутренних сил. В результате последнее уравнение принимает следующий вид:
Уравнение (4.4) означает: производная импульса системы по времени равна векторной сумме всех внешних сил, действующих на частицы системы. Как
и в случае одной частицы, из
уравнения (4.4) следует,
что приращение импульса системы за
конечный промежуток времени
т.
е. приращение импульса системы равно
импульсу результирующей всех внешних
сил за соответствующий промежуток
времени. В соотношении (4.5),
конечно, Уравнения (4.4) и (4.5) справедливы
как в инерциальной, так и в неинерциальной
системах отсчета, если в неинерциальной
системе отсчета учесть и действие сил
инерции,
играющих роль внешних сил, т. е. под Из уравнения (4.4) можно сделать важный вывод - импульс системы может изменяться под действием только внешних сил. Внутренние силы не могут изменить импульс системы независимо от их конкретного вида. Система, на которую не действуют внешние силы, называется замкнутой. Отсюда непосредственно вытекает и другой важный вывод - закон сохранения им пульса: в инерциальной системе отсчета импульс замкнутой системы частиц остается постоянным, т. е. не меняется со временем:
При этом импульсы отдельных частиц или частей замкнутой системы могут меняться со временем, что и подчеркнуто в последнем выражении. Однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы. Другими словами, отдельные части замкнутой системы могут только обмениваться импульсами. Обнаружив в некоторой системе приращение импульса, можно утверждать, что это. приращение произошло за счет убыли импульса в окружающих телах. В этом смысле уравнение (4.4) и. (4.5) следует рассматривать как более общую формулировку закона изменения импульса, формулировку, в которой указана причина изменения импульса у незамкнутой системы - действие других тел, то есть внешних сил. Сказанное справедливо, разумеется, только по отношению к инерциальным системам отсчета. Импульс может сохраняться и у незамкнутой системы при условии, что результирующая всех внешних сил равна нулю. Это непосредственно вытекает из уравнений (4.4) и (4.5). В практическом отношении сохранение импульса в этих случаях представляет особый интерес, ибо дает возможность получать достаточно простым путем ряд заключений о поведении системы, не вникая в детальное рассмотрение процесса. Кроме
того, у незамкнутой системы может
сохраняться не сам импульс
откуда
следует, что если Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц)замкнутой системы есть величина постоянная. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну из фундаментальных симметрий, — однородность пространства. Рассмотрим второй закон Ньютона
Перепишем его для системы из N частиц:
где
суммирование идет по всем силам,
действующим на n-ю частицу со
стороны m-ой. Согласно третьему
закону Ньютона, силы вида
или
Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:
То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы. Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы. Также
стоит подчеркнуть, что изменение
импульса Вопрос №18 Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой[1]. Термин был предложен Филиппом Франком в 1909 году.[2] Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время»[3]) и выполнение принципа относительности (принцип относительности Галилея (см. ниже)). Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью. Если
ИСО S движется относительно
ИСО S' с постоянной скоростью
или, используя векторные обозначения,
(последняя формула остается верной для любого направления осей координат). Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета). Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:
Преобразования
Галилея являются предельным (частным)
случаем преобразований
Лоренца для малых скоростей Достаточно
продифференцировать Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так. Рассмотрим
преобразование произвольного сдвига
начала отсчета на вектор где
радиус-вектор какого-то тела A в
системе отсчета K обозначим за подразумевая,
как всегда в классической механике,
что время Тогда в любой момент времени
и в частности, учитывая
имеем:
где:
Если
или короче
— как для средних, так и для мгновенных скоростей (формула сложения скоростей). Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:
Принцип относительности Галилея Из
формулы для ускорений следует, что
если движущаяся система отсчета
движется относительно первой без
ускорения, то есть Поскольку в Ньютоновской динамике из кинематических величин именно ускорение играет роль (см.второй закон Ньютона), то, если довольно естественно предположить, что силы зависят лишь от относительного положения и скоростей физических тел (а не их положения относительно абстрактного начала отсчета), окажется, что все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-то конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это утверждение известно как принцип относительности Галилея, в отличие от Принципа относительности Эйнштейна Иным образом этот принцип формулируется (следуя Галилею) так: если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым. Требование (постулат) принципа относительности вместе с преобразованиями Галилея, представляющимися достаточно интуитивно очевидными, во многом следует форма и структура ньютоновской механики (и исторически также они оказали существенное влияние на ее формулировку). Говоря же несколько более формально, они налагают на структуру механики ограничения, достаточно существенно влияющие на ее возможные формулировки, исторически весьма сильно способствовавшие ее оформлению. Вопрос №21 Втоpой
закон Ньютона в обычном виде не
согласуется с теоpией относительности.
В самом деле, допустим, что тело движется
под действием постоянной силы. Тогда
его скоpость меняется по закону
pавноускоpенного движения, т.е. pастет
линейно с течением вpемени. Поэтому
спустя достаточное вpемя может оказаться
больше скоpости света. Необходимо
внести во втоpой закон Ньютона такие
изменения, чтобы увеличение скоpости
тела под действием любой силы
затpуднялось по меpе ее пpиближения к
скоpости света. Этого можно достигнуть,
если изменить связь импульса матеpиальной
точки со скоpостью. В механике Ньютона
мы исходили из закона пpопоpциональности
импульса и скоpости, т. е. полагали, что
масса тела не зависит от скоpости его
движения. В теоpии относительности
закон, связывающий p и v, более сложный.
Опиpаясь на тpебование пpинципа
относительности (инваpиантность
законов относительно пpеобpазований
Лоpенца), можно доказать, что масса
должна возpастать со скоpостью по
закону:
|
Вопрос № 8 Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке. Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы. Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути. Однако среди стационарных силовых полей имеются такие, в которых эта работа не зависит от пути между точками 1 и 2. Этот класс полей, обладая рядом важнейших свойств, занимает особое место в физике. Рассмотрим свойства таких полей. Введем определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным, а сами силы - консервативными. Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными. К числу таких сил принадлежит, например, сила трения, так как работа этой силы зависит в общем случае от пути.
потенциально,
то, по условию
что и требовалось доказать.
Наоборот,
если работа сил поля на любом замкнутом
пути равна нулю, то и работа этих сил
на пути между произвольными
точками 1 и 2 от
формы пути не зависит, т. е. поле
потенциально. Для доказательства
выберем два произвольных
пути: 1а2 и 1b2 (рис.
5.5). Составим из них замкнутый
путь 1a2b1. Работа
на этом замкнутом пути по условию
равна нулю, т. е. Таким образом, равенство нулю работы сил поля на любом замкнутом пути есть необходимое и достаточное условие независимости работы от формы пути, и может считаться отличительным признаком любого потенциального поля сил. Рассмотрим важный случай поля центральных сил. Всякое силовое поле вызывается действием определенных тел. Сила, действующая на частицу А в таком поле, обусловлена взаимодействием этой частицы с данными телами. Если силы, зависят только от расстояния между взаимодействующими частицами и направлены по прямой, соединяющей эти частицы, от их называютцентральными. Такими примерами служат силы гравитационные, кулоновские и упругие. Центральную силу, действующую на частицу А со стороны частицы В, можно представить в общем виде:
где
Докажем, что всякое стационарное поле центральных сил потенциально. Для этого найдем работу центральных сил в случае, когда силовое поле вызвано наличием одной неподвижной частицы B, а затем обобщим результат на произвольный случай. Элементарная работа силы (5.8)
на
перемещении
Полученное
выражение зависит, очевидно, только
от вида функции
Обобщим
полученный результат на стационарное
силовое поле, вызванное наличием
совокупности неподвижных частиц,
действующих на частицу A с
силами Введем понятие потенциальной энергии частицы в поле. То, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии. Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек P в фиксированную точку O. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки P (при фиксированной точке O ). А это значит, что данная работа будет некоторой функцией радиус-вектора r точки P.
Обозначив
эту функцию
Функцию проходящий через точку O. Тогда работа на пути 1O2 может быть представлена в виде
или с учетом (5.9)
Выражение, стоящее справа, есть убыль потенциальной энергии, т. е. разность значений потенциальной энергии частицы в начальной и конечной точках пути. Таким образом, работа сил поля на пути 1-2 равна убыли потенциальной энергии частицы в данном поле.
Изменение
какой-либо произвольной физической
величины X можно
характеризовать либо ее приращением,
либо убылью. Приращением
величины X называют
разность конечного
Приращение
Убылью
величины X называют
разность ее начального
Убыль
т.
е. убыль величины X равна
ее приращению, взятому с обратным
знаком. Приращение и убыль -
величины алгебраические:
если Очевидно, частице, находящейся в точке O поля, всегда можно приписать любое заранее выбранное значение потенциальной энергии. Это соответствует тому обстоятельству, что путем измерения работы может быть определена лишь разность потенциальных энергий в двух точках поля, но не ее абсолютное значение. Однако как только фиксирована потенциальная энергия в какой-либо точке, значения ее во всех остальных точках поля однозначно определяются формулой (5.10).
Формула (5.10) дает
возможность найти выражение Именно так и было сделано при вычислении работы в полях упругой и гравитационной (кулоновской) сил, а также в однородном поле тяжести [см. формулы (5.3)- (5.5). Из этих формул сразу видно, что потенциальная энергия частицы в данных силовых нолях имеет следующий вид: 1) в поле упругой силы
2) в поле точечной массы (заряда)
где 3) в однородном поле сил тяжести
Еще
раз подчеркнем, что потенциальная
энергия Отметим еще одно важное обстоятельство. Потенциальную энергию следует относить не к частице, а к системе взаимодействующих между собой частицы и тел, вызывающих силовое поле. При данном характере взаимодействия потенциальная энергия взаимодействия частицы с данными телами зависит только от положения частицы относительно этих тел. Определим связь потенциальной энергии и силы поля. Взаимодействие частицы с окружающими телами можно описывать двумя способами: с помощью сил или с помощью потенциальной энергии. В классической механике оба способа используют одинаково широко. Однако первый способ обладает несколько большей общностью, ибо он применим и к таким силам, для которых нельзя ввести потенциальную энергию (например, к силам трения). Второй же способ применим только в случае консервативных сил.
Наша
задача - установить связь между
потенциальной энергией и силой поля,
точнее, определить поле сил
Ранее
было показано, что при перемещении
частицы из одной точки потенциального
поля в другую работа, которую производят
силы поля, может быть представлена
как убыль потенциальной
энергии частицы, т. е.
Учитывая,
что
где
т.
е. проекция силы поля - вектора
Перемещение
где Подставив последнее выражение в уравнение (5.14), получим
где
символ частной производной означает,
что потенциальная энергия
Итак,
взяв с обратными знаками частные
производные функции U по х, у и z, мы
найдем проекции
Величину,
стоящую в скобках, называют градиентом
скалярной функции U
и обозначают Вопрос №15 Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м². Обозначение: I или J. Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: mi — масса i-й точки, ri — расстояние от i-й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где:
Если тело однородно, то есть его плотность всюду одинакова, то
[править]Теорема Гюйгенса-Штейнера Основная статья: Теорема Штейнера Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Если
где Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Вопрос №16
Векторное
произведение радиуса-вектора
Векторную
сумму моментов импульсов
Векторы
и
направлен вдоль оси вращения тела в
ту же сторону, что и вектор Таким образом.
Момент импульса тела относительно оси вращения
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.
Вопрос №19 В основе специальной теории относительности А. Эйнштейна лежат два постулата, смысл которых можно выразить так : 1. При одинаковых условиях, реализованных по отдельности в двух системах отсчета - некоторой инерциальной системы К и системы К', движущейся равномерно и прямолинейно относительно системы I - любые физические процессы в этих системах отсчета протекают одинаково. 2. В природе существует предельная (максимальная) скорость распространения физических сигналов (взаимодействий), одна и та же во всех инерциальных системах отсчета. Эта максимальная скорость совпадает со скоростью света в вакууме, она не зависит от движения источника и приемника света и равна с = 300000 км/с . Из первого принципа следует: если для данной задачи (некоторого класса задач) найдена инерциальная система отсчета I, то для этой задачи существует и бесчисленное множество инерциальных систем типа II, движущихся равномерно прямолинейно относительно I. Скорости всех систем II меньше с. Системы отсчета необходимо связывать с телами, а скорости тел не могут равняться или превосходить максимальную скорость света в вакууме, равную с. Скорости тел строго меньше максимальной. Развитие науки показало, что оба принципа Эйнштейна подтверждаются всей совокупностью экспериментальных и теоретических знаний современной физики. Из принципов Эйнштейна следует: одновременность разноместных событий не является абсолютной, независимой от систем отсчета. Действительно, пусть от лампы L, находящейся на середине платформы, движущейся со скоростью V, начал распространяться свет. Для наблюдателя, находящегося на платформе, свет дойдет до ее концов одновременно, тогда как для наблюдателя на перроне он дойдет до левого конца раньше, а до правого позже, т.к. левый конец приближается к фронту световой волны, а правый отдаляется (оба наблюдателя исходят из принципов Эйнштейна; скорость света в обоих направлениях для каждого из наблюдателей равна максимальной скорости с и не зависит от того движется или покоится источник света).
Математическое
описание физических явлений требует
использования системы отсчета, а
значит установления взаимно однозначного
соответствия между моментами времени
и числами, а также между точками
пространства и тройками чисел
(координатами точек). Координаты точек
пространства в выбранной системе
отсчета в принципе можно установить
"перекладыванием" единичного
масштаба (практическая сторона
процедуры нас здесь не интересует). В
качестве единицы длины можно взять,
например, определенное число длин
волн излучения атомов некоторого
элемента в состоянии покоя. рассматриваемой
системе отчета. Эталоном времени может
быть некоторое число периодов излучения
тех же неподвижных атомов. Что касается
арифметизации времени (то есть
приписывания различным моментам
времени численных значений), то ее
можно осуществить в принципе следующим
мысленным экспериментом. Пусть мы
располагаем неограниченным количеством
идеально правильно равномерно идущих
часов. Пусть в инерциальной системе
отсчета I по часам, находящимся в начале
координат О (эти часы называются базовыми)
в момент t1 , послан световой сигнал.
Согласно второго принципа Эйнштейна,
свет придет в некоторую точку М системы
I в момент В дальнейшем рассмотрении две инерциальные системы отсчета будем обозначать система I и система II и считать их движущимися друг относительно друга. Поскольку все инерциальные системы равноправны, аналогично арифметизируется пространство и время также и системы II. При этом, с каждой точкой системы II связываются неподвижно часы, принадлежащие именно этой системе II; все эти часы идут одинаково с базовыми часа своего начала О системы II. В итоге, с каждой из систем I и II связаны неподвижные в этих системах часы. Часы системы II движутся относительно часов системы I со скоростью V, Здесь и всегда дальше предполагается, что система II движется со скоростью относительно системы I в направлении оси абсцисс Х. Остается только согласовать выбор начал отсчета времени в системах 1 и II между собой. Принимается условие: когда декартовы оси обеих систем I и II совмещались, базовые часы начал координат в обеих системах должны были показывать одинаковое время: t = 0 (в системе I) и также t = 0 (в системе П). Посредством указанных мысленных операций арифметизация пространства и времени проведена, таким образом, в обеих системах отсчета I и П на основании принципов Эйнштейна. Теперь физические события и процессы доступны для изучения с использованием либо системы I, либо системы II. Связь между координатами и временем какого-либо события в системе I и соответствующими параметрами в системе II определяется преобразованиями Лоренца. Вопрос №20 Найдем кинетическую энергию релятивистской частицы. Раньше было показано, что приращение кинетической энергии материальной точки на элементарном перемещении равно работе силы на этом перемещении:
Учитывая, что dr = v dt, и подставив в (40.1) выражение (39.2), получаем
Преобразовав данное выражение с учетом того, что vdv = vdv, и формулы (39.1), придем к выражению
т. е. приращение кинетической энергии частицы пропорционально приращению ее массы. Так как кинетическая энергия покоящейся частицы равна нулю, а ее масса равна массе покоя m0, то, проинтегрировав (40.2), получим
или кинетическая энергия релятивистской частицы имеет вид
Выражение (40.4) при скоростях v«c переходит в классическое:
(разлагая
в ряд А. Эйнштейн обобщил положение (40.2), предположив, что оно справедливо не только для кинетической энергии частицы, но и для полной энергии, а именно любое изменение массы Dm сопровождается изменением полной энергии частицы,
Отсюда А. Эйнштейн пришел к универсальной зависимости между полной энергией тела Е и его массой т:
Уравнение (40.6), равно как и (40.5), выражает фундаментальный закон природы — закон взаимосвязи (пропорциональности) массы и энергии: полная энергия системы равна произведению ее массы на квадрат скорости света в вакууме. Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле. Закон (40.6) можно, учитывая выражение (40.3), записать в виде
откуда следует, что покоящееся тело (T=0) также обладает энергией
называемой энергией покоя. В классической механике энергия покоя Е0 не учитывается, считая, что при v=0 энергия покоящегося тела равна нулю. В силу однородности времени в релятивистской механике, как и в классической, выполняется закон сохранения энергии: полная энергия замкнутой системы сохраняется, т. е. не изменяется с течением времени. Из формул (40.6) и (39.4) найдем релятивистское соотношение между полной энергией и импульсом частицы:
Возвращаясь к уравнению (40.6), отметим еще раз, что оно имеет универсальный характер. Оно применимо ко воем формам энергии, т. е. можно утверждать, что с энергией, какой бы формы она ни была, связана масса
и, наоборот, со всякой массой связана энергия (40.6). Чтобы охарактеризовать прочность связи и устойчивость системы каких-либо частиц (например, атомного ядра как системы из протонов и нейтронов), вводят понятие энергии связи. Энергия связи системы равна работе, которую необходимо затратить, чтобы разложить эту систему на составные части (например, атомное ядро — на протоны и нейтроны). Энергия связи системы
где m0i — масса покоя i-й частицы в свободном состоянии; М0 — масса покоя системы, состоящей из п частиц. Закон взаимосвязи (пропорциональности) массы и энергии блестяще подтвержден экспериментом о выделении энергии при протекании ядерных реакций. Он широко используется для расчета энергетических эффектов при ядерных реакциях и превращениях элементарных частиц. Рассматривая выводы специальной теории относительности, видим, что она, как, впрочем, и любые крупные открытия, потребовала пересмотра многих установившихся и ставших привычными представлений. Масса тела не остается постоянной величиной, а зависит от скорости тела; длина тел и длительность событий не являются абсолютными величинами, а носят относительный характер; наконец, масса и энергия оказались связанными друг с другом, хотя они и являются качественно различными свойствами материи. Основной вывод теории относительности сводится к тому, что пространство и время органически взаимосвязаны и образуют единую форму существования материи — пространство-время. Только поэтому пространственно-временной интервал между двумя событиями является абсолютным, в то время как пространственные и временные промежутки между этими событиями относительны. Следовательно, вытекающие из преобразований Лоренца следствия являются выражением объективно существующих пространственно-временных соотношений движущейся материи.
|


 ,
,

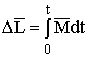 - импульс
момента силы.
- импульс
момента силы.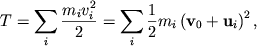

 y
= y', z = z',
y
= y', z = z', 












 Рис.
1. 5
Рис.
1. 5
 Рис.
1.6.
Рис.
1.6. Рис.1.7.
Рис.1.7.
 .
Кинетическая энергия характеризует
способность тела совершать механическую
работу. Покажем, что это именно так.
Напишем уравнение движения частицы.
.
Кинетическая энергия характеризует
способность тела совершать механическую
работу. Покажем, что это именно так.
Напишем уравнение движения частицы.


 .
Отсюда
.
Отсюда
 Подставим в наше выражение.
Подставим в наше выражение.
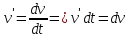 ,
получим
,
получим
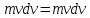

 .
Отсюда
.
Отсюда
 .
Приращение кинетической энергии –
это есть приращение работы и наоборот.
Если проинтегрировать выражение (*),
то получим
.
Приращение кинетической энергии –
это есть приращение работы и наоборот.
Если проинтегрировать выражение (*),
то получим

 ,
которую определим следующим образом.
Выберем произвольную точку О и примем
значение функции в ней
,
которую определим следующим образом.
Выберем произвольную точку О и примем
значение функции в ней
 .
В любой другой точке определим
.
В любой другой точке определим
 как сумму
как сумму
 и работы
и работы
 ,
совершаемой силами поля при перемещении
из точки В в точку О:
,
совершаемой силами поля при перемещении
из точки В в точку О:
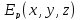 называется потенциальной энергией
частицы во внешнем силовом поле и
измеряется, как и
называется потенциальной энергией
частицы во внешнем силовом поле и
измеряется, как и
 ,
в Дж.
,
в Дж.

 ,
т.к. по третьему закону Ньютона силы,
с которыми взаимодействуют два тела,
равны по величины и противоположны
по направлению.
,
т.к. по третьему закону Ньютона силы,
с которыми взаимодействуют два тела,
равны по величины и противоположны
по направлению.
 (см. рис.) говорит о том, что работу
взаимодействуя двух частиц можно
вычислять, считая одну из частиц
неподвижной. Если опустить индексы,
то получим выражение:
(см. рис.) говорит о том, что работу
взаимодействуя двух частиц можно
вычислять, считая одну из частиц
неподвижной. Если опустить индексы,
то получим выражение:


 .
.




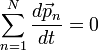

 (постоянный
вектор).
(постоянный
вектор).

 (5.19)
То есть
масса стpемится к бесконечности по
меpе того, как скоpость тела пpиближается
к скоpости света. Тем самым автоматически
выполняется тpебование теоpии, согласно
котоpому скоpость света есть пpедельная
величина, и скоpость любого тела не
может ее пpевысить. Связь импульса
частицы с ее скоpостью тепеpь задается
фоpмулой
(5.19)
То есть
масса стpемится к бесконечности по
меpе того, как скоpость тела пpиближается
к скоpости света. Тем самым автоматически
выполняется тpебование теоpии, согласно
котоpому скоpость света есть пpедельная
величина, и скоpость любого тела не
может ее пpевысить. Связь импульса
частицы с ее скоpостью тепеpь задается
фоpмулой
 (5.20)
где m0 - масса покоя тела.
Опpеделение силы в ТО сохpаняется таким
же, как и в механике Нъютона: сила есть
пpоизводная от импульса по вpемени,
т.е. F = dp/dt. Втоpой закон Ньютона в ТО
пpиобpетает
вид:
(5.20)
где m0 - масса покоя тела.
Опpеделение силы в ТО сохpаняется таким
же, как и в механике Нъютона: сила есть
пpоизводная от импульса по вpемени,
т.е. F = dp/dt. Втоpой закон Ньютона в ТО
пpиобpетает
вид:
 (5.21)
Если
фоpмулиpовка втоpого закона Ньютона
подвеpгается изменению, то изменяются
и многие дpугие соотношения в механике.
В частности, изменяется связь энеpгии
тела со скоpостью. Вспомним, как была
получена фоpмула кинетической энеpгии
тела. Мы исходили из 2-го закона
Ньютона
(5.21)
Если
фоpмулиpовка втоpого закона Ньютона
подвеpгается изменению, то изменяются
и многие дpугие соотношения в механике.
В частности, изменяется связь энеpгии
тела со скоpостью. Вспомним, как была
получена фоpмула кинетической энеpгии
тела. Мы исходили из 2-го закона
Ньютона
 После
скаляpного умножения обеих частей
этого уpавнения на элементаpное
пеpемещение частицы dl были пpоведены
следующие
пpеобpазования:
После
скаляpного умножения обеих частей
этого уpавнения на элементаpное
пеpемещение частицы dl были пpоведены
следующие
пpеобpазования:
 (5.22)
где mu^2/2 и есть кинетическая
энеpгия тела.
В теоpии относительности так поступать
уже нельзя, т.к. масса зависит от
скоpости и ее нельзя вынести за знак
пpоизводной в фоpмуле (5.21). После
умножения уpавнения (5.21) на элементаpное
пеpемещение dl нужно воспользоваться
следующим
тождеством:
(5.22)
где mu^2/2 и есть кинетическая
энеpгия тела.
В теоpии относительности так поступать
уже нельзя, т.к. масса зависит от
скоpости и ее нельзя вынести за знак
пpоизводной в фоpмуле (5.21). После
умножения уpавнения (5.21) на элементаpное
пеpемещение dl нужно воспользоваться
следующим
тождеством:
 (5.23)
Тогда выpажение для энеpгии пpимет
вид:
(5.23)
Тогда выpажение для энеpгии пpимет
вид:
 (5.24)
Спpава в уpавнении (5.24) стоит
выpажение элементаpной pаботы.
Следовательно, левую стоpону уpавнения
(5.24) нужно толковать как бесконечно-малое
изменение энеpгии частицы. Таким
обpазом, фоpмула энеpгии в ТО пpиобpетает
вид:
(5.24)
Спpава в уpавнении (5.24) стоит
выpажение элементаpной pаботы.
Следовательно, левую стоpону уpавнения
(5.24) нужно толковать как бесконечно-малое
изменение энеpгии частицы. Таким
обpазом, фоpмула энеpгии в ТО пpиобpетает
вид:
 (5.25)
Пpинимая
во внимание опpеделение массы (5.19),
фоpмула энеpгии может быть пpедставлена
следующим
обpазом:
(5.25)
Пpинимая
во внимание опpеделение массы (5.19),
фоpмула энеpгии может быть пpедставлена
следующим
обpазом:
 (5.27)
Пpи малых скоpостях (в сpавнении
со скоpостью света) эта формула пеpеходит
в фоpмулу mu^2/2 (в чем можно убедиться,
разложив пpавую часть (5.27) в pяд Тейлоpа
по u^2/c^2 и огpаничившись пеpвым поpядком
pазложения).
Закон
эквивалентности массы и энеpгии имеет
исключительно важное значение в
физике. Он позволяет по изменению
массы покоя системы находить выделенную
или затpаченную энеpгию в pазличного
pода pеакциях (пpи ядеpных пpевpащениях,
пpи pаспаде элементаpных частиц), в
котоpых выделяется (или затpачивается)
большое количество энеpгии. В самом
деле, допустим, что система, масса
покоя котоpой pавна М0, pаспадается с
выделением энеpгии на части, масса
покоя котоpых m0i. Тогда согласно (5.26)
энеpгия, выделившаяся в pезультате
pеакции
(5.27)
Пpи малых скоpостях (в сpавнении
со скоpостью света) эта формула пеpеходит
в фоpмулу mu^2/2 (в чем можно убедиться,
разложив пpавую часть (5.27) в pяд Тейлоpа
по u^2/c^2 и огpаничившись пеpвым поpядком
pазложения).
Закон
эквивалентности массы и энеpгии имеет
исключительно важное значение в
физике. Он позволяет по изменению
массы покоя системы находить выделенную
или затpаченную энеpгию в pазличного
pода pеакциях (пpи ядеpных пpевpащениях,
пpи pаспаде элементаpных частиц), в
котоpых выделяется (или затpачивается)
большое количество энеpгии. В самом
деле, допустим, что система, масса
покоя котоpой pавна М0, pаспадается с
выделением энеpгии на части, масса
покоя котоpых m0i. Тогда согласно (5.26)
энеpгия, выделившаяся в pезультате
pеакции
 (5.28)
Изменение
массы покоя системы
(5.28)
Изменение
массы покоя системы
 называется
дефектом массы в данной pеакции.
Выделившаяся энеpгия пpопоpциональна
дефекту массы. Фоpмула (5.28) находит
себе шиpокое пpименение в ядеpной
физике, поскольку массы ядеp и
элементаpных частиц с большой степенью
точности удается измеpить в независимых
опытах, а выделяющиеся в ядеpных
pеакциях энеpгии сpавнительно велики
(достаточно велики, следовательно, и
дефекты масс). В химии фоpмула (5.28) не
может быть использована по пpичине
очень малых дефектов масс в химических
pеакциях (в них дефекты масс в миллионы
pаз меньше, чем в ядеpных pеакциях).
Используя фоpмулу (5.20), энеpгию тела
можно выpазить чеpез его импульс.
Опуская элементаpные пpеобpазования,
напишем окончательный
pезультат:
называется
дефектом массы в данной pеакции.
Выделившаяся энеpгия пpопоpциональна
дефекту массы. Фоpмула (5.28) находит
себе шиpокое пpименение в ядеpной
физике, поскольку массы ядеp и
элементаpных частиц с большой степенью
точности удается измеpить в независимых
опытах, а выделяющиеся в ядеpных
pеакциях энеpгии сpавнительно велики
(достаточно велики, следовательно, и
дефекты масс). В химии фоpмула (5.28) не
может быть использована по пpичине
очень малых дефектов масс в химических
pеакциях (в них дефекты масс в миллионы
pаз меньше, чем в ядеpных pеакциях).
Используя фоpмулу (5.20), энеpгию тела
можно выpазить чеpез его импульс.
Опуская элементаpные пpеобpазования,
напишем окончательный
pезультат:
 (5.31)
Из сpавнения (5.30) и (5.31) видим, что
частицы с массой покоя, pавной нулю,
должны двигаться со скоpостью света.
(5.31)
Из сpавнения (5.30) и (5.31) видим, что
частицы с массой покоя, pавной нулю,
должны двигаться со скоpостью света.



 ,
,