10. Уравнение Шредингера, волновая функция

Общее временное уравнение Шредингера, позволяющее определить в любой момент времени волновую функцию   для частицы массы  , движущейся в силовом поле  , описываемом скалярной потенциальной функцией  , имеет вид     

.

(3.8)

Здесь   - мнимая единица, а   - рационализированная постоянная Планка. Стандартным символом   в (3.8) обозначен дифференциальный оператор Лапласа, который в декартовой системе координат имеет вид

   

.

(3.9)

В общем случае в задачах квантовой механики дифференциальное уравнение в частных производных (3.8) должно решаться с учетом определенных начальных и граничных условий на волновую функцию.

Начальное условие задает значение волновой функции в начальный момент времени  .

Граничные условия являются следствием регулярности волновой функции, обеспечивая, в частности, ее непрерывность. Эти условия формулируются на границах областей, где потенциальная функция  терпит разрывы первого или второго рода. Сюда же относятся условия на волновую функцию в бесконечно удаленных точках пространства, которые обеспечивают выполнение условия нормировки (3.4).

Уравнение Шредингера, как и законы классической механики Ньютона, законы термодинамики, уравнения электродинамики Максвелла и другие основные физические уравнения, не может быть выведено из других соотношений. Его следует рассматривать как некоторое научное положение, справедливость которого доказывается согласием результатов расчетов, выполненных с помощью уравнения Шредингера, с данными экспериментов. Такое согласие установлено для большого числа явлений в атомной и ядерной физике. Квантовые эффекты, предсказанные с помощью уравнения Шредингера, лежат в основе многих технических устройств, приборов и технологий.

Уравнение Шредингера тесно связано с гипотезой де Бройля и вытекающим из неё корпускулярно-волновым дуализмом материи. Действительно, непосредственной проверкой легко убедиться, что для свободной частицы, с кинетической энергий 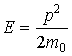 , движущейся в отсутствие силовых полей ( ) в направлении оси  , решением соответствующего уравнения Шредингера

     

(3.10)

является волновая функция   

,

(3.11)

соответствующая плоской волне де Бройля. Этот факт позволяет утверждать, что и в общем случае уравнение Шредингера является волновым уравнением. Линейность этого уравнения обуславливает принцип суперпозиции квантовых состояний, физическое содержание которого обсуждалось в предыдущем параграфе.

Как уже указывалось, квантовая механика содержит в себе классическую механику как некоторый предельный случай. Значит, соответствующий предельный переход можно осуществить и в основном уравнении квантовой механики. Уравнение Шредингера после такого предельного преобразования должно перейти в основное уравнение классической механики.

11. Решение уравнения Шредингера для потенциальной ямы

Если поместить частицу в потенциальную яму, то непрерывный спектр энергий становится дискретным. Для уравнения (1)

 с потенциальной энергией  , которая равна нулю в интервале   и становится бесконечной в точках   и  . На этом интервале уравнение Шрёдингера совпадает с (4).

Граничные условия (2), (3) 

для волновой функции запишутся в виде

Ищем решения в виде  . С учётом граничных условий получаем для собственных значений энергии 

и собственных функций с учётом нормировки
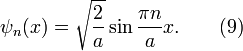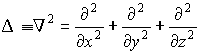