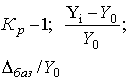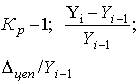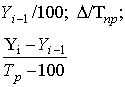Основные показатели рядов динамики. Система средних показателей.
При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут: 1) абсолютный прирост, 2) темпы роста, 3) темпы прироста, 4) абсолютное значение одного процента прироста.
Расчет показателей динамики представлен в следующей таблице.
Показатель |
Базисный |
Цепной |
Абсолютный
прирост |
Yi-Y0 |
Yi-Yi-1 |
Коэффициент роста (Кр) |
Yi : Y0 |
Yi : Yi-1 |
Темп роста (Тр) |
(Yi : Y0)×100 |
(Yi : Yi-1)×100 |
Коэффициент прироста (Кпр )** |
|
|
Темп прироста (Тпр) |
|
|
Абсолютное значение одного процента прироста (А) |
|
|
*
* 
** 
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.
Методы выравнивания рядов динамики.
Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ - на исследовании линейной диаграммы.
Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:
1) используя полусумму уровней, расположенных рядом с интерполируемыми;
2) по среднему абсолютному приросту;
3) по темпу роста.
Выявление сезонных колебаний.
Метод аналитического выравнивания используется для изучения сезонных колебаний.
Сезонными называются периодические колебания, возникающие под влиянием смены времени года.
Для познания закономерностей развития социально-экономических явлений во внутригодовой динамике необходимо иметь количественные характеристики развития изучаемых явлений по месяцам и кварталам годового цикла.
Сезонные колебания присутствуют во всех сферах жизни общества: в производстве, обращении, потреблении. Большое значение сезонные колебания приобретают в изучении покупательского спроса населения на отдельные товары и виды услуг, а также на изменение цен и инфляцию. Цель изучения сезонных колебаний – это прогнозирование и разработка оперативных мер по управлению их развитием во времени.
Сезонные колебания характеризуются индексами сезонности. Для выявления сезонных колебаний обычно берут данные за ряд лет, чтобы выявить устойчивую сезонную волну. Если ряд динамики содержит определенную тенденцию в развитии явления, то сначала осуществляют аналитическое выравнивание ряда, затем сравнивают фактические теоретические уровни. Индекс сезонности в этом случае равен
где n – число лет, за которые даны уровни;
уф – фактические данные;
Уt – теоретические данные.
Расчет сезонных колебаний можно выполнять другим методом в зависимости от характера динамики.
Если годовой уровень явления из года в год остается относительно неизменным, то индексы сезонности исчисляются по формуле
.
Для сопоставления величины сезонных колебаний по нескольким предприятиям или периодам может быть использовано среднее квадратическое отклонение, исчисляемое по формуле
где n – число месяцев;
Jсез. – индекс для каждого месяца.
Чем меньше среднее квадратическое отклонение, тем меньше величина сезонных колебаний.