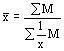12. Понятие средней. Средняя арифметическая и средняя арифметическая взвешенная. Свойства средней.

Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Средние величины исчисляются для характеристики уровня цен, заработной платы, основного капитала, численности населения и др. однородной совокупности социально-эко­номических явлений.

Требования, предъявляемые к средним величинам:

–   средняя должна характеризовать качественно однородную совокупность;

–   средние должны исчисляться по данным большого числа единиц, составляющих совокупность, то есть отображать массовые социально-экономические явления.

Для более глубокого научного анализа изучаемых явлений исчисляют средние величины не только всей совокупности, но и по составляющим эту совокупность. Задача статистики состоит в том, чтобы дать смысловую социально-экономическую оценку результатам расчетов средних показателей.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у единиц совокупности.

В экономических исследованиях применяются две категории средних: степенные средние и структурные средние.

Таблица 3.1

Виды средних величин

Наименование  средней	Формула средней
	Простая	Взвешенная
Арифметическая

  При расчетах средней арифметической выделяются ее основные свойства:

- среднее от постоянной величины равна ей самой;

- произведение средней на сумму частот равно сумме произведений вариант на частоты;

- изменение каждого варианта на одну и ту же величину изменяет среднюю величину на эту же величину;

- изменение каждого варианта на одно и тоже число изменяет среднюю во столько же раз;

- изменение каждой частоты в одно и то же число раз не изменяет величину средней;

- алгебраическая сумма отклонений всех вариантов от средней равна 0.

   Определение средней арифметической по данным интервального вариационного ряда происходит следующим образом, – для каждого ряда определяется среднее значение интервала как полусумма его нижнего и верхнего значения вариант, а далее расчет ведется по формуле средней арифметической взвешенной. Средняя гармоническая величина. Это величина обратная среднеарифметической. Она применяется, когда известны отдельные значения варьирующего признака и вся совокупность признаков, а частоты неизвестны. Существует два вида среднегармонической.

13. Средняя гармоническая, степенные виды средних. Структурные средние.

Гармоническая

Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Средняя гармоническая вычисляется в тех случаях, когда в качестве весов применяются не единицы совокупности, а произведения этих единиц на значения признака (то есть М=хf).

Средняя гармоническая простая исчисляется в тех случаях, когда веса одинаковы, то есть равны между собой.

Средняя геометрическая простая используется при вычислении среднего коэффициента роста (темпа роста) в рядах динамики.

Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).

В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.

Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:

 ,
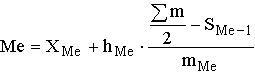