Сферическая функция
,
;
;
;
1.
Описывает
угловую зависимость состояния объекта
в сферических координатах
.
2. Описывает вращательное движение в теории излучения и рассеяния волн и частиц, в теории потенциала.
3. Определяется как собственная функция оператора момента импульса и оператора Лапласа.
4. Число l связано с модулем момента импульса.
5.
Число m
связано с проекцией момента импульса
на ось z.
Проекция вектора не может быть больше
его модуля, поэтому
,
для проекции возможны положительные и
отрицательные значения.
6.
Набор
образует полный ортонормированный
базис функций на единичной сфере.
Момент импульса частицы
В классической механике
,
– радиус-вектор
частицы,
– импульс. Направление L
перпендикулярно
и
,
и определяется правилом
правого винта.
В декартовых координатах
,
,
,
.
Формулы переходят друг в друга при циклической перестановке
.
В квантовой механике величины заменяются операторами
,
,
.
Оператор градиента
В декартовых координатах оператор градиента
,
(7.1)
где nk – единичные орты, направленные в сторону перемещения точки при бесконечно малом увеличении соответствующего аргумента.
Действуем
на функцию
оператором градиента, получаем вектор
.
Модуль показывает быстроту увеличения функции, а направление показывает сторону наибольшего возрастания функции.
Операторы момента импульса
В декартовых координатах
,
,
,
.
(7.2)
Формулы переходят друг в друга при циклической перестановке
.
Сферические координаты
,
,
.
(7.3)
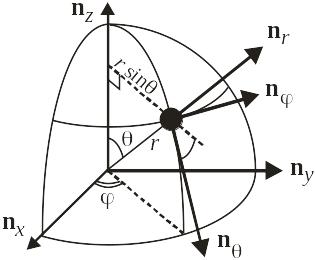
Оператор градиента
,
(П.8.1)
где
– единичные орты.
Операторы момента импульса
,
(7.4)
.
(7.5)
Оператор Лапласа
В декартовых и сферических координатах оператор Лапласа
,
(7.6)
определяет кинетическую энергию частицы.
Радиальная часть оператора Лапласа
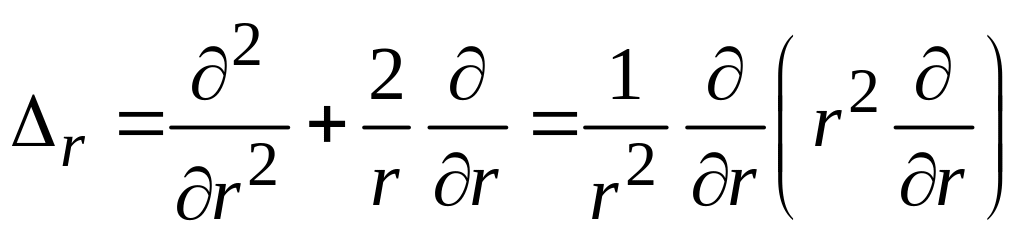(7.7)
определяет кинетическую энергию радиального движения.
Угловая часть оператора Лапласа
определяет энергию вращательного движения. Это слагаемое создает центробежную силу отталкивания от оси вращения, поэтому относится к потенциальной энергии. Этим объясняется знак минус.
Перестановочное соотношение операторов (коммутатор)
Коммутатор определяется в виде
.
Предполагается, что правее каждого слагаемого находится функция, на которую действуют операторы:
.
Выполняются
,
.
Необходимо
следить за порядком следования операторов,
переставлять можно только взаимно
коммутирующие операторы, например:
.
Физический
смысл коммутатора.
Если операторы коммутируют
,
то их можно переставлять, соответствующие
им физические величины измеримы
одновременно с неограниченной точностью.
Это объясняется совместимостью физических
приборов, выполняющих измерение. Если
операторы не коммутируют
,
то чем точнее измеряется одна величина,
тем больше неустранимая погрешность
другой величины. Соответствующие
физические приборы, выполняющие
измерения, взаимно не совместимы.
Для операторов момента импульса выполняются
,
,
,
.
(7.8)
Следовательно,
определенные значения одновременно
имеют квадрат модуля момента импульса
и одна из его проекций, например,
.