Связанные состояния электрона в АтомЕ водорода Атом протия

1. Ядро – тяжелый протон с зарядом +е. Оболочка – легкий электрон с зарядом –е и массой μ. Считаем, что электрон движется вокруг неподвижного ядра. Электрическое поле ядра сферически симметричное. Для упрощения решения используем сферические координаты с центром в ядре. Электрон атома находится в стационарном состоянии с постоянной полной энергией и определенным орбитальным моментом. Полная энергия связанного состояния отрицательная.

2. Потенциальная энергия электрона в СГС

, .

3. Кинетическая энергия радиального движения электрона в атоме

,

– радиальный импульс.

4. Кинетическая энергия углового движения

,

где

L – орбитальный момент;

– момент инерции электрона;

– орбитальное квантовое число.

5. Полная энергия связанного электрона

.

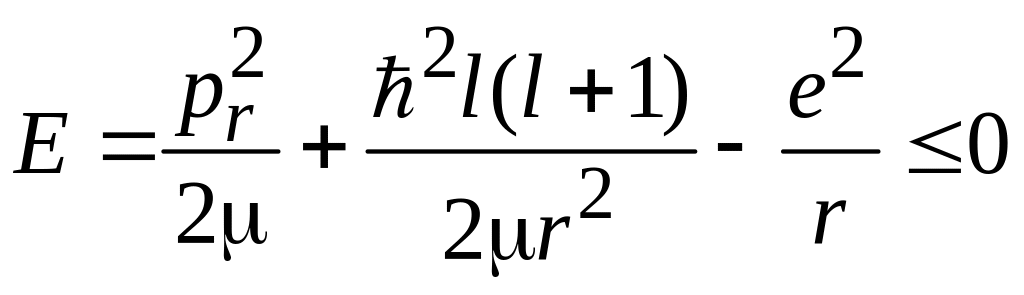6. С учетом выражаем квадрат радиального импульса

.

Уравнение Шредингера

Радиальное и угловое движения электрона в атоме независимы друг от друг. У волновой функции электрона разделены зависимости от радиальной и угловых переменных

.

Радиальная функция удовлетворяет стационарному уравнению Шредингера

,

где в сферических координатах

.

Подставляем и получаем уравнение

. (6.84)

Требуется найти спектр возможных значений Е и функцию .

Упростим уравнение, перейдя от размерного аргумента r к безразмерному аргументу x, и от энергии Е к числу n.

Переход к безразмерным величинам

1. Из мировых постоянных строится боровский радиус атома водорода

Å.

2. Энергию E заменяем на безразмерную величину n

,

тогда

.

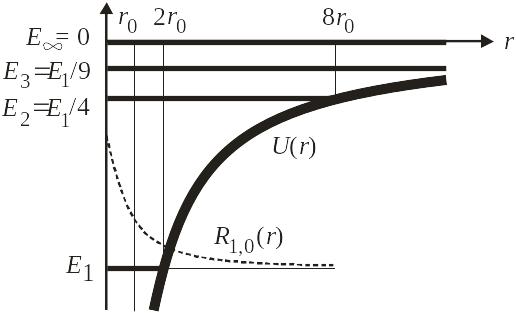
Далее доказано, что число n квантуется , и спектр энергии связанного электрона дискретный:

– основное состояние с наименьшей энергией,

,

,

.

При электрон отрывается от ядра атома и становится свободным. При спектр энергии электрона непрерывный.

Уравнение (6.84)

после замены

,

получает вид

.

3. Координату r заменяем безразмерной x

,

используем

,

,

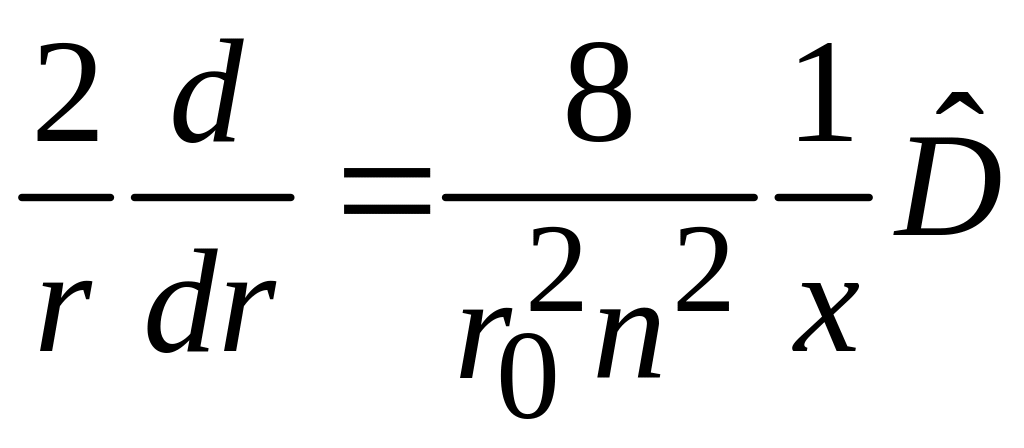где

– оператор дифференцирования.

Уравнение умножаем на и получаем

, (6.85)

где

; .

Требуется найти и спектр n.

Решение методом факторизации

1. Уравнение обобщенного гипергеометрического типа (5.5)

,

где

,

сравниваем с (6.85).

2. Получаем

, , , .

Для функций

, ,

находим

, ,

, .

Сравниваем и .

Для Q получаем

.

Решаем квадратное уравнение и находим

.

Для S получаем

,

откуда

.

Для R и получаем

,

,

.

3. Учет области определения аргумента x от до дает

,

следовательно

, .

После устранения двузначности δ и η находим

,

,

,

,

.

4. Из (5.8)

получаем весовую функцию

.

5. Если кратность дифференцирования – целое не отрицательное число, то применима формула Родрига (5.7)

.

С учетом

,

,

, .

находим решение

.

Оператор кратного дифференцирования того же вида имеет обобщенный полином Лагерра

.

Выражаем оператор через полином Лагерра

,

где

,

.

В результате радиальная функция электрона

. (6.85а)

Если – не целое, то нормировка не существует и физическое состояние отсутствует. Это доказывает целочисленность n и квантование энергии связанного электрона

.

6. Используем условие ортонормированности (5.11) в методе факторизации

, .

Подставляем

,

,

,

, ,

.

Получаем

,

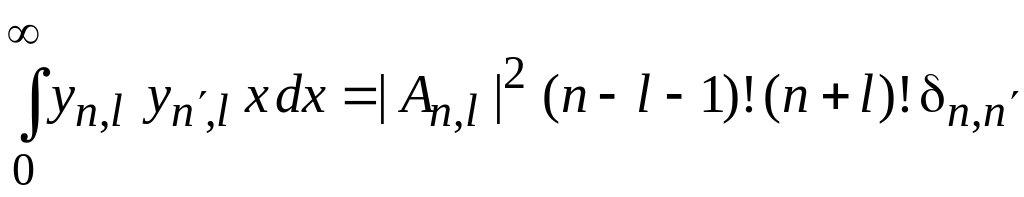или, с учетом

, ,

находим

.

Выбираем из требования

. (6.86)

тогда

.

Из (6.85а)

получаем нормированное решение уравнения Шредингера

, (6.87)

где

, , .