Полиномы низших степеней
Из (6.42)
и
(6.44) при
получаем
,
,
,
.
При
находим обычные полиномы Лагерра
,
,
,
.
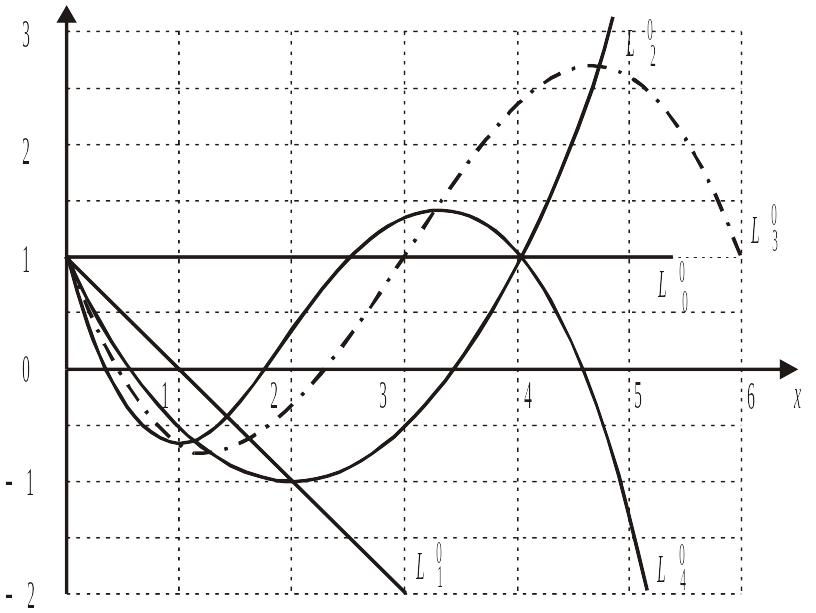
Производящая функция
Методом факторизации ранее получено
.
(6.52)
По определению (5.14)
с учетом получаем
.
(6.53)
Рекуррентные соотношения
1. Дифференцируем (6.52) по x
.
Подставляем (6.53)
.
Приравниваем
коэффициенты при
и находим
.
(6.54)
2. Дифференцируем (6.54) далее, и получаем
,
.
(6.55)
При
находим
.
Заменяем
и получаем выражение обобщенного
полинома Лагерра через полином Лагерра
.
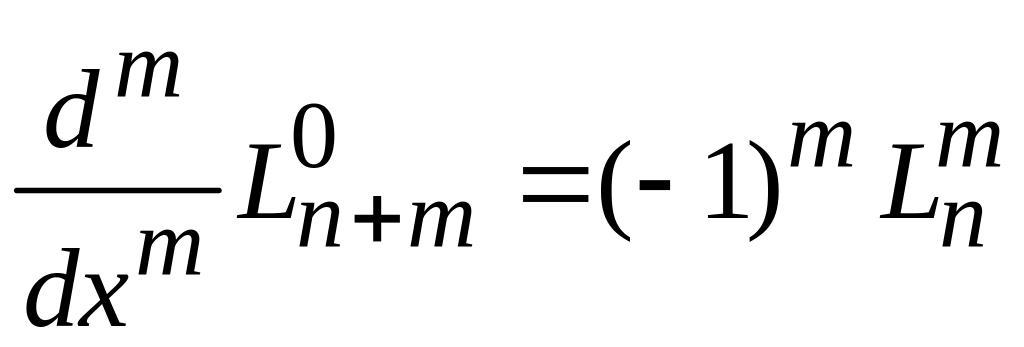(6.56)
3. В уравнение Лагерра (6.41)
подставляем (6.54)
,
,
где , и получаем
.
(6.57)
Производящую функцию (6.52)
дифференцируем по t и приходим к уравнению
.
Подставляем (6.53)
,
получаем
.
Приравниваем коэффициенты при
.
Приводим подобные
.
(6.58)
5. Из (6.52)
следует
.
Подставляем (6.53)
,
получаем
.
Приравниваем коэффициенты при
.
(6.59)
6. В (6.58)
перегруппировываем слагаемые
.
Используем (6.59)
,
,
получаем
.
(6.60)
Заменяем
и
.
(6.61)
7. Из (6.58) в виде
вычитаем (6.61) и получаем
.
(6.64)
Ортонормированность
Методом факторизации ранее получено (П.3.11). Доопределяем и получаем
.
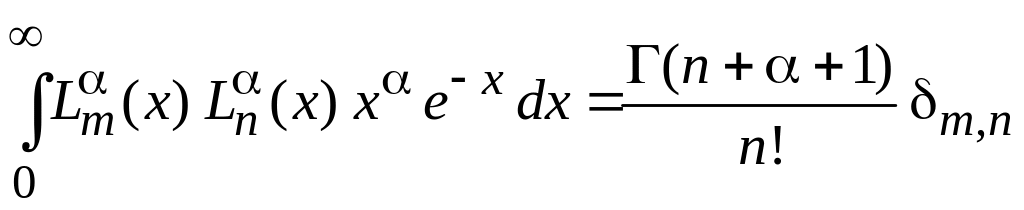(6.67)
Разложение функции по ортонормированному базису
Множество
функций
,
где
;
α – фиксировано;
,
образует полный ортонормированный
базис. Функцию
,
определенную при
,
разлагаем по базису
.
(6.68)
Ищем
коэффициент разложения, проектируя в
пространстве функций уравнение (6.68) на
вектор
.
Для этого умножаем (6.68) на
и интегрируем
.
Учитываем
ортонормированность (6.67). За счет символа
Кронекера в сумме остается лишь одно
слагаемое. После замены
получаем
.
Подстановка (6.42)
дает
.
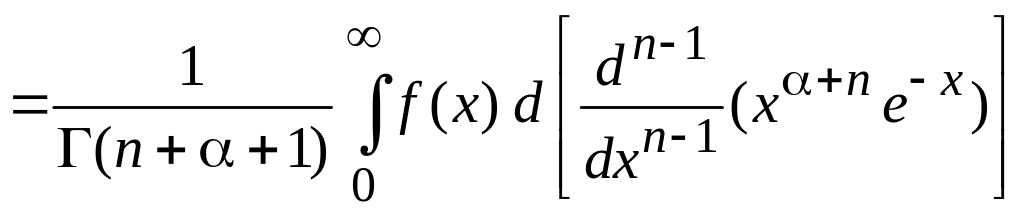Интегрируем по частям n раз, свободные слагаемые равны нулю на обоих пределах. Получаем коэффициент
.
(6.69)
Интегралы с полиномами Лагерра
1. Вычисляем
,
r
– целое.
Подстановка (6.42)
дает
.
Интегрируем по частям n раз и получаем
,
где учтено
.
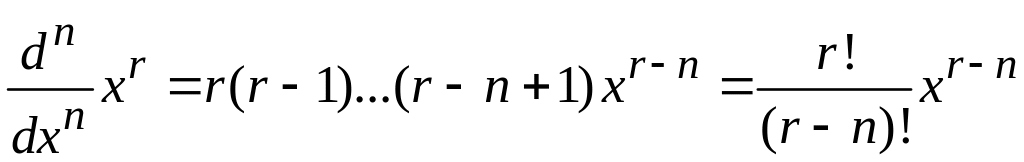Используем формулу гамма-функции (4.1)
,
находим
,
,
(6.70)
,
.
(6.71)
Из
(6.70) при
и
,
(6.72)
.
(6.73)
2. Вычисляем
,
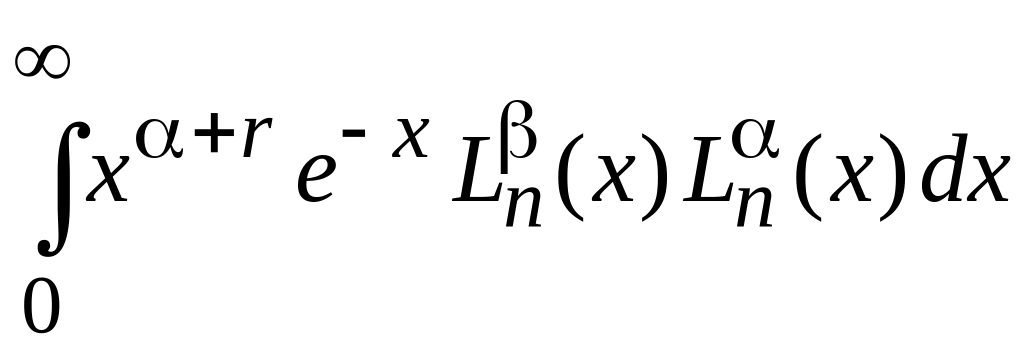r
– целое.
Подстановкой полиномиальной формы (6.44)
,
интеграл сводится к (6.70)
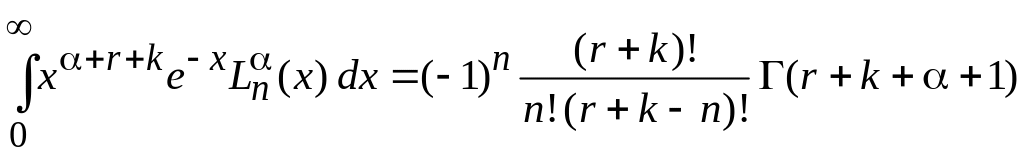
В результате получаем
=
.
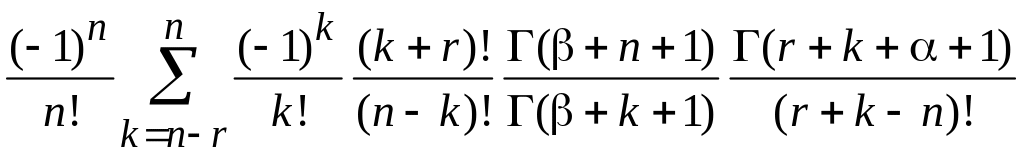(6.74)
Ограничение
нижнего предела суммирования по k
вызвано множителем
.
При
в сумме (6.74) остается одно слагаемое
и результат не зависит от величины β
,
(6.75)
что доказывает нормировку в условии ортонормированности (6.67), полученном методом факторизации:
.
При
из (6.74) получаем
.
(6.76)
3. Вычисляем интеграл
,
r
– целое,
,
отличающийся от (6.70) знаком перед r.
В (6.70)
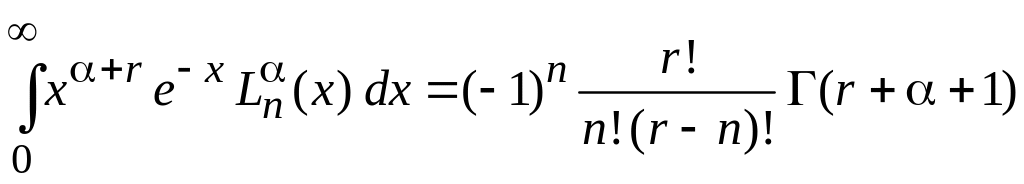
заменяем
,
где
.
Учитываем
,
где использовано (4.4)
.
Равенство (6.70) после замены получает вид
,
.
(6.77)
Из (6.77) при и находим
,
,
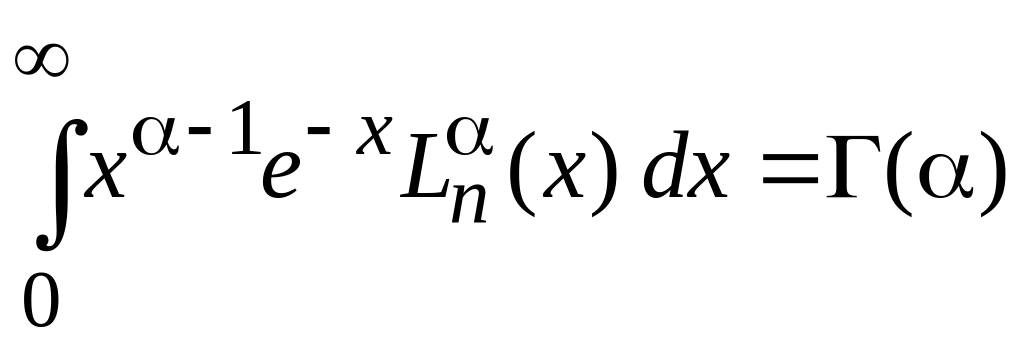(6.79)
,
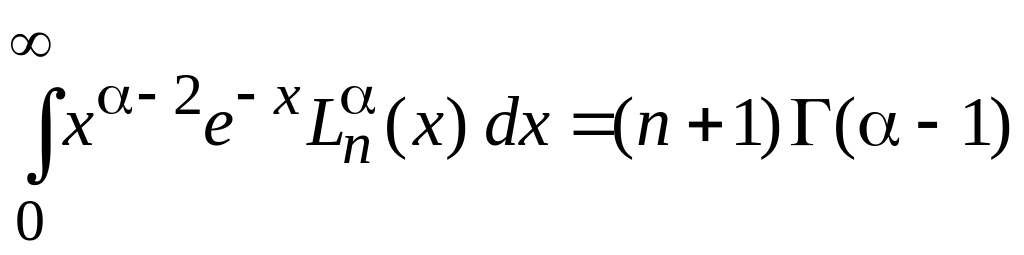(6.80)
4. Вычисляем
,
r
– целое.
Интеграл сводится к (6.77)
если использовать (6.44):
.
Получаем
.
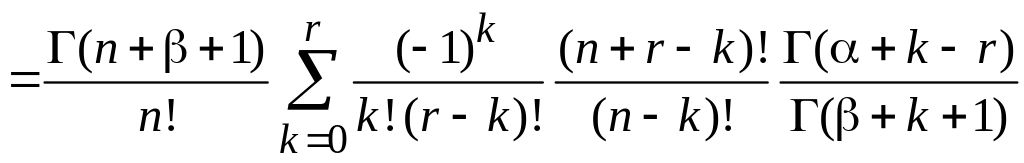(6.81)
При и
,
(6.82)
.
(6.83)