2. Функцию (6.32)

дифференцируем

.

Учитываем (6.12)

,

,

,

Получаем

. (6.35)

Соотношение устраняет дифференцирование функции . Из (6.35) находим

, (6.36)

следовательно,

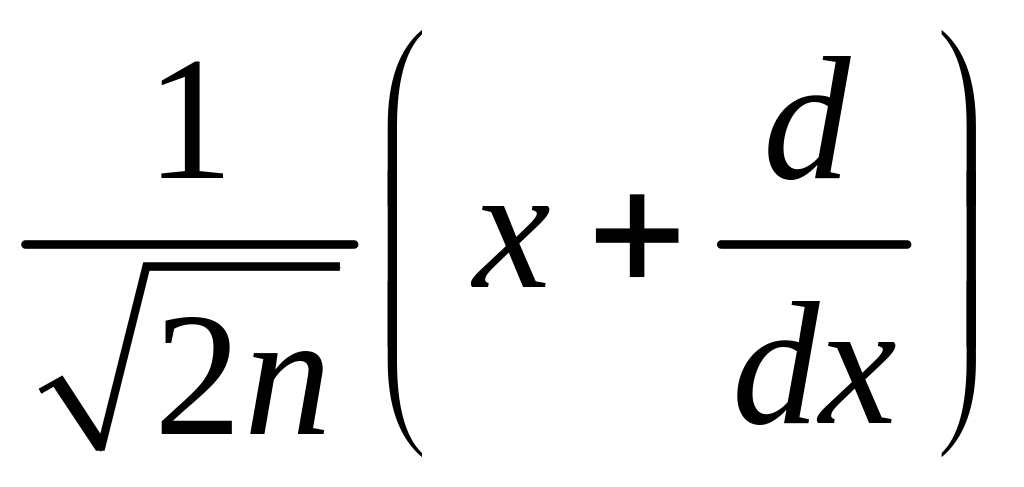– оператор перехода между состояниями путем уничтожения кванта энергии .

3. Из (6.34)

выражаем

.

Подстановка в (6.35)

дает

. (6.37)

Из (6.37) находим

, (6.38)

следовательно,

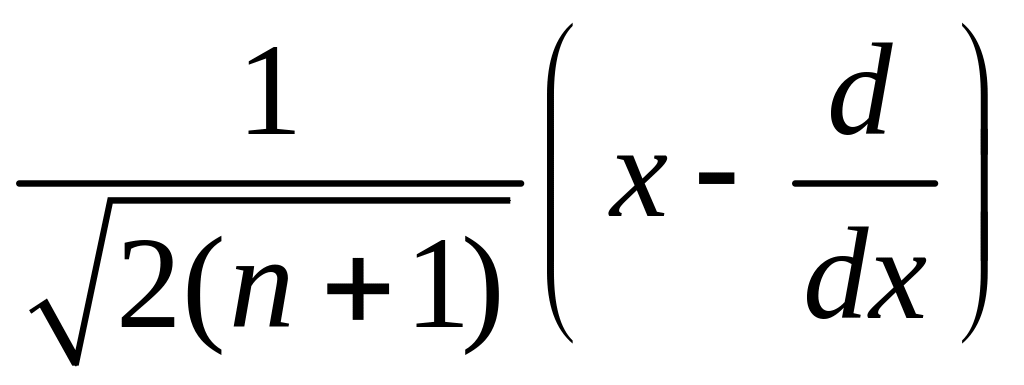– оператор перехода между состояниями путем рождения кванта энергии .

4. Складываем (6.37) и (6.35)

,

получаем

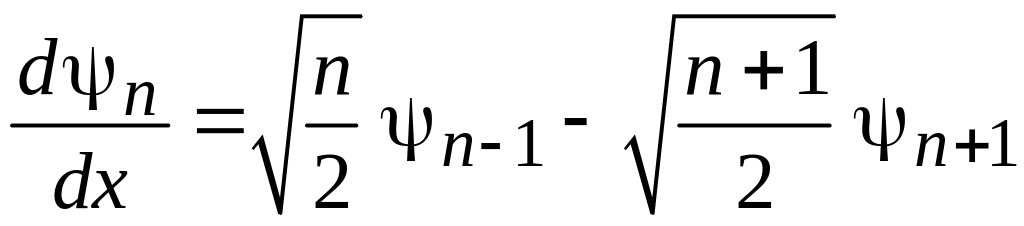. (6.39)

Соотношение используется при вычислении матричных элементов.

Матрица перехода между состояниями

Множество состояний системы с разным числом квантов энергии образует дискретный ортонормированный базис функций . Возмущение, действующее на систему и описываемое оператором , переводит систему из некоторого состояния , в общем случае, в множество состояний с разной вероятностью. Совокупность дискретных состояний системы и результатов воздействия на них выражают:

матрица начального состояния

,

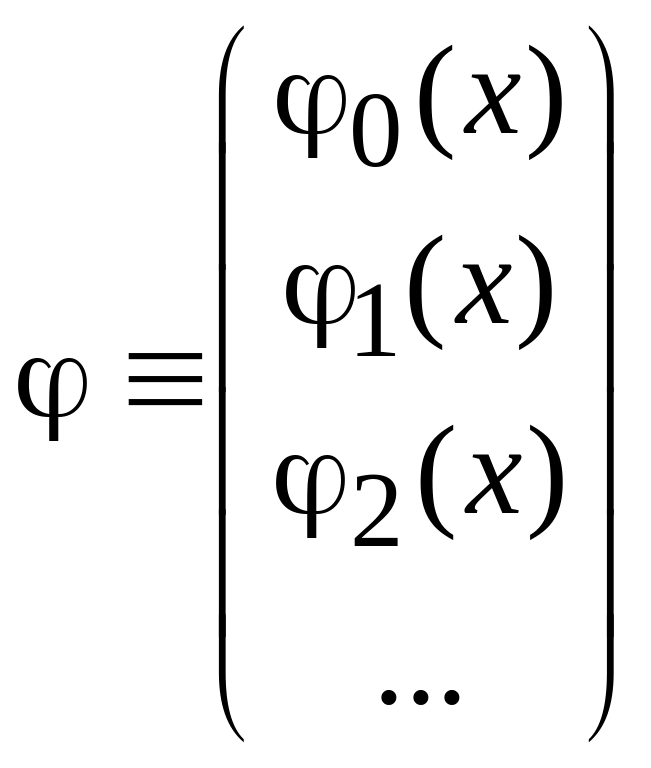матрица конечного состояния

,

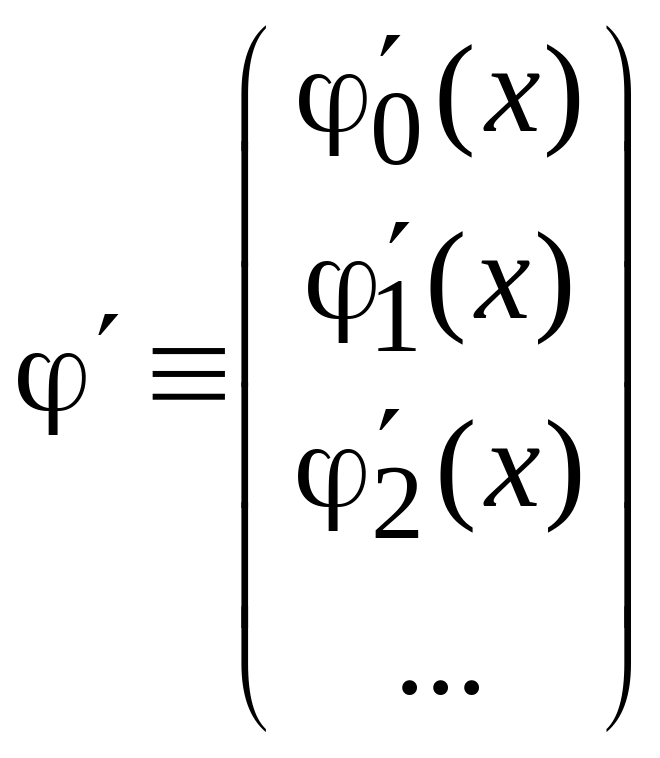матрица перехода

,

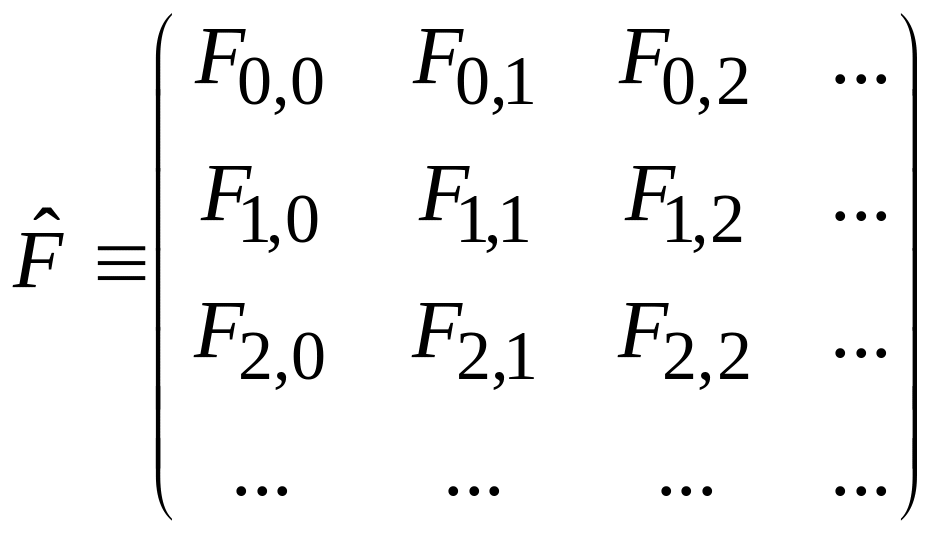тогда

.

Матричный элемент

Матричный элемент является мерой перехода системы между двумя состояниями под действие оператора . По индексам переход происходит справа налево, k – начальное состояние, n – конечное состояние.

В пространстве функций с базисом , определенном на интервале (A, B), и весовой функцией матричный элемент оператора между ортами и определяется в виде скалярного произведения

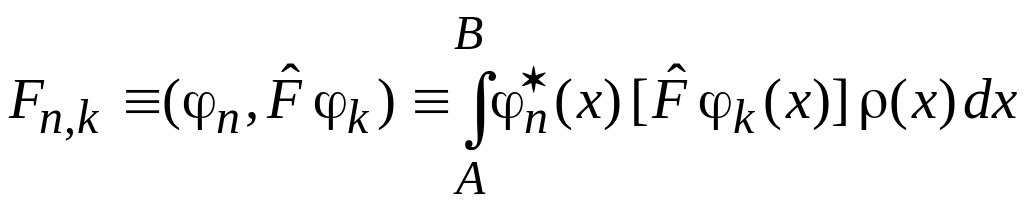, (1)

где A, B, – вещественные.

Физический смысл матричного элемента

Диагональный матричный элемент

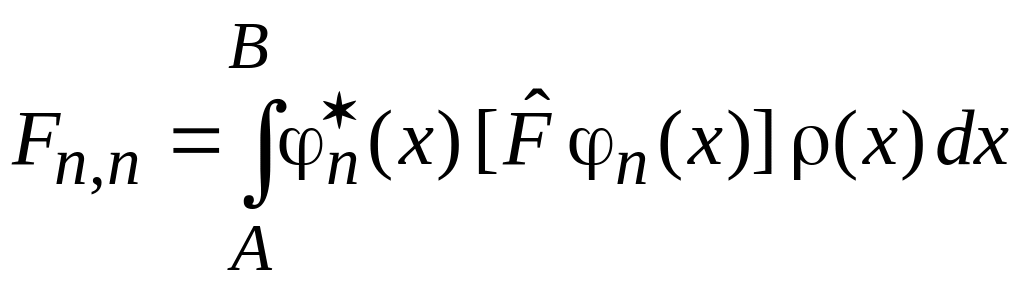
есть среднее значение величины f, описываемой оператором , в состоянии .

Недиагональный матричный элемент

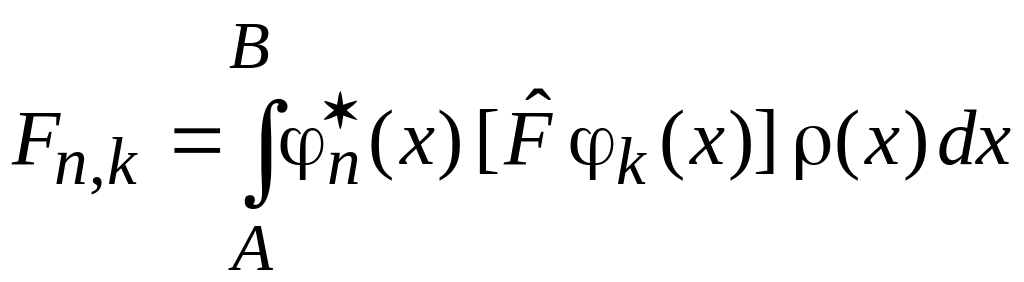
есть амплитуда вероятности перехода между состояниями под действием оператора .

Вероятность перехода равна квадрату модуля матричного элемента

.

В результате матричные элементы являются измеримыми величинами. Рассмотрим частные случаи оператора .

Операторы координаты и импульса

Любая физическая величина, кроме времени, описывается оператором, в частности, операторы координаты и импульса равны

,

,

где – постоянная Планка. Для безразмерной координаты получаем

, ,

, .

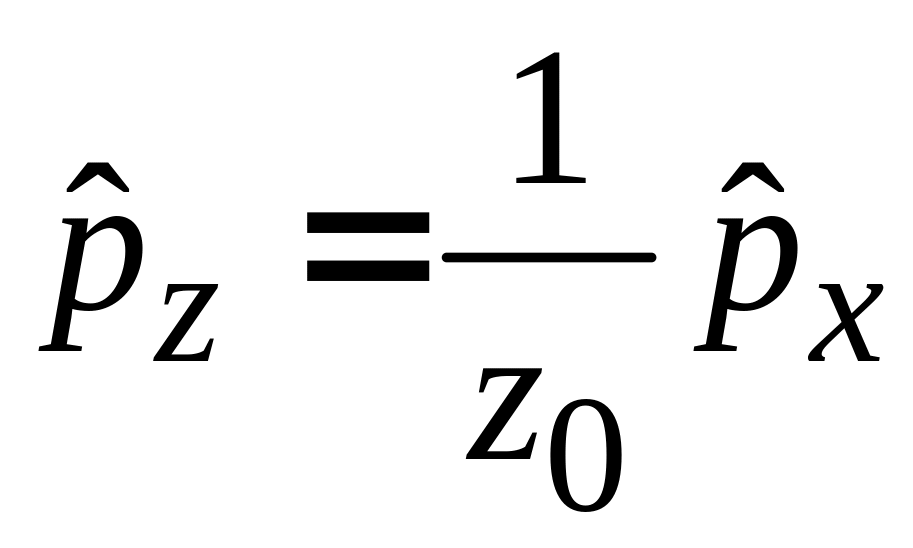Эрмитовый оператор

Оператор физической величины эрмитовый, т. е. удовлетворяет:

, (2)

где «+» – операция эрмитового сопряжения. Условие (2) обеспечивает вещественность собственных значений оператора, т. е. результатов измерения соответствующей физической величины.

Эрмитово сопряжение оператора возникает при его переносе в скалярном произведении от одной функции к другой функции

,

.

Эрмитовый оператор, удовлетворяющий , переносится в скалярном произведении функций от одного сомножителя к другому без изменения

,

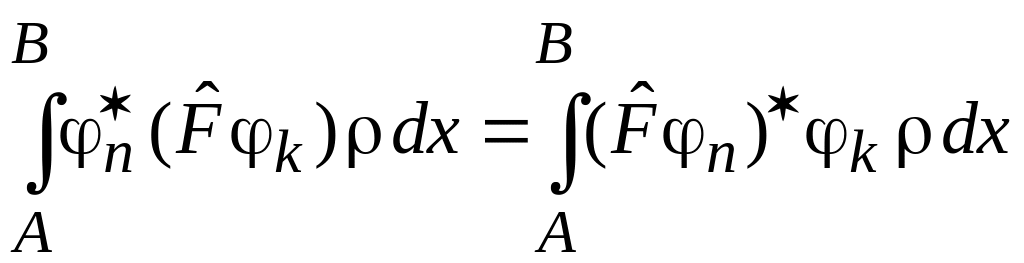. (3)