Уравнение Шредингера

Состояние стационарной системы с энергией Е описывается волновой функцией

.

Ее получают из уравнения Шредингера

.

Для осциллятора используем (6.30б)

,

получаем

.

Для получения упрощаем уравнение, переходя к безразмерной координате:

,

где

– амплитуда колебаний классического осциллятора с энергией , тогда

, ,

,

Для

,

с учетом

,

получаем уравнение обобщенного гипергеометрического типа

, (6.31)

Методом факторизации ранее получено решение (П.3.6)

. (6.32)

Из (6.3)

и (6.32) находим

.

Четность функции состояния совпадает с четностью номера состояния n.

– основное состояние – четное,

– первое возбужденное состояние – нечетное.

Получим постоянную в (6.32), используя свойства функции состояния.

Физический смысл функции состояния

Квадрат модуля волновой функции равен плотности вероятности обнаружения частицы, т. е. вероятности ее обнаружения в единичном интервале координат около точки z:

Вероятность найти частицу в интервале

.

Вероятность найти частицу во всем пространстве

.

Для осциллятора вещественно и , тогда получаем условие нормировки функции состояния

.

Условие ортонормированности

Из (П.3.7)

,

полученного методом факторизации, следует

.

Полагаем

,

получаем

,

где x – безразмерная координата. В результате

,

. (6.32а)

С размерной координатой условие ортонормированности

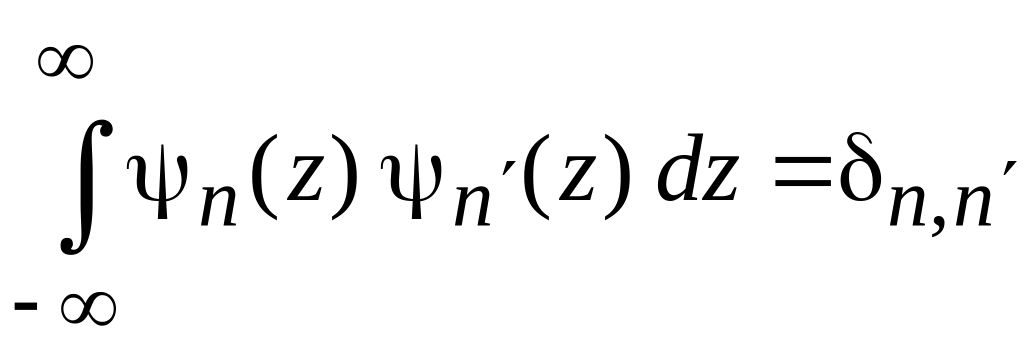. (6.33)

Учитываем

, , .

Из (6.32а) находим основное состояние с наименьшей энергией

, (6.33а)

и первое возбужденное состояние с энергией

. (6.33б)

Графики функций , и показаны на рисунке.

В точках поворота (6.30а)

классический осциллятор с полной энергией останавливается. Подставляем и получаем

,

, , .

Точки поворота показаны на рисунке черными кругами. Классическая частица не может их перейти. Для квантовой частицы решение за пределами этих точек не равно нулю. Следовательно, квантовую частицу можно обнаружить в области, не доступной классической частице. Это явление называется туннельным эффектом. Оно основано на соотношении неопределенностей Гейзенберга, которое следует из теоремы Фурье о частотной полосе – чем уже область, доступная для движения частицы, тем больше неопределенность ее импульса. За счет флуктуации импульса частица продвигается в область с большей потенциальной энергией, чем ее исходная полная энергия.

Рекуррентные соотношения для

1. Используем рекуррентное соотношение для полиномов Эрмита (6.15)

.

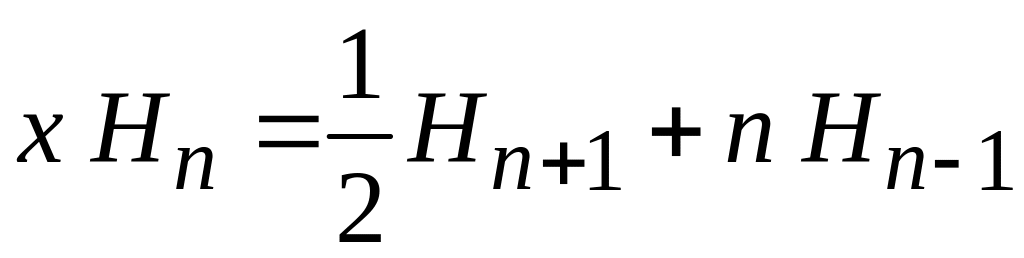Умножаем его на

.

Используем (6.32)

,

где

,

тогда

,

.

получаем

. (6.34)

Соотношение (6.34) позволяет устранить множитель x перед функцией .