Примеры

1. Найти среднее расстояние электрона от ядра в состоянии с квантовыми числами .

С учетом оператора радиуса и радиального объема , находим

,

где сделана замена . Вычисляем интеграл с помощью рекуррентного соотношения (6.89), устраняющего x под интегралом:

– ,

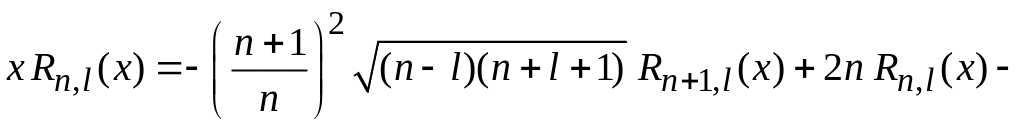
и условия ортонормированности (6.86)

.

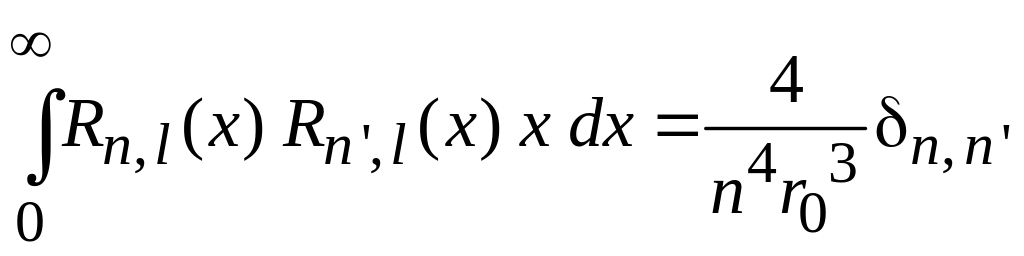При возведении в квадрат рекуррентного соотношения и интегрировании условие ортогональности зануляет перекрестные произведения благодаря символу Кронекера , остается сумма квадратов слагаемых

.

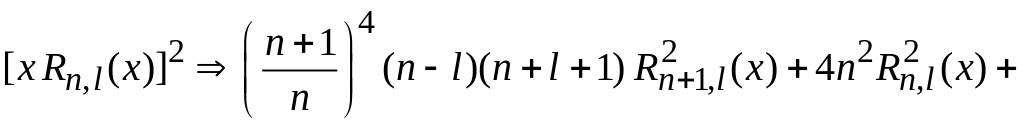
С учетом нормировки (6.86)

,

,

,

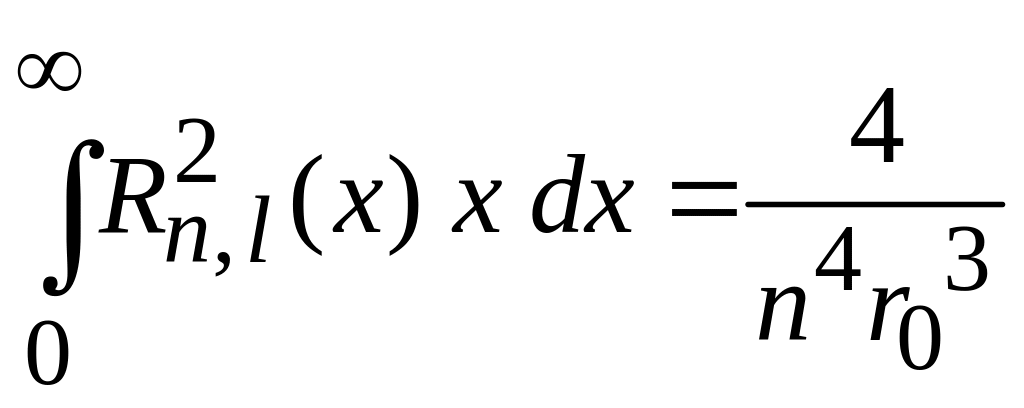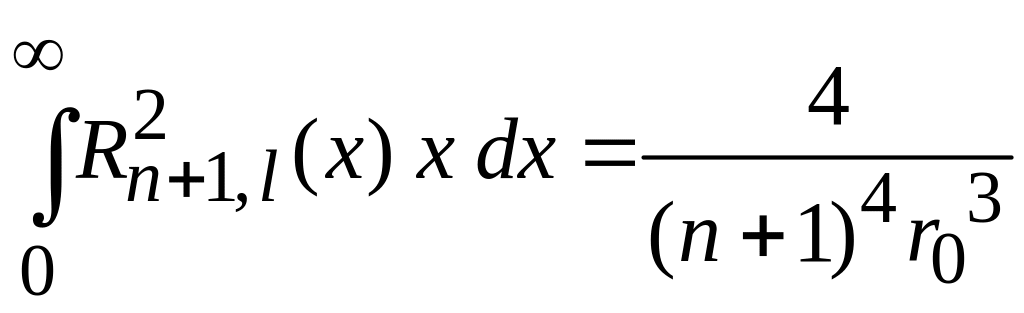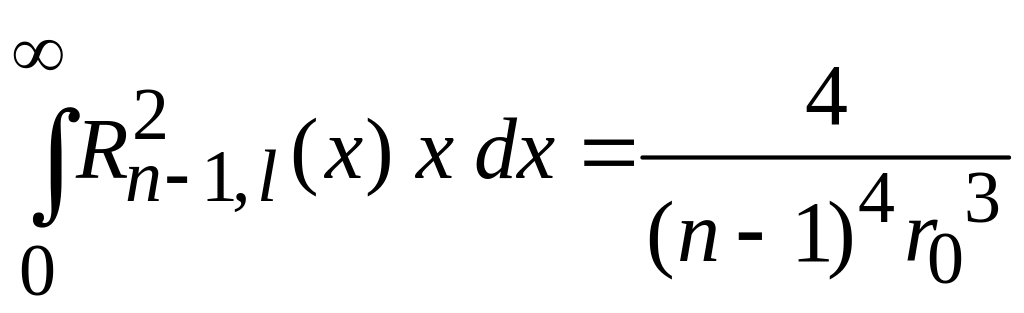находим

.

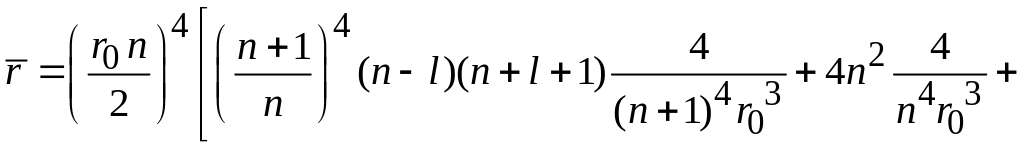
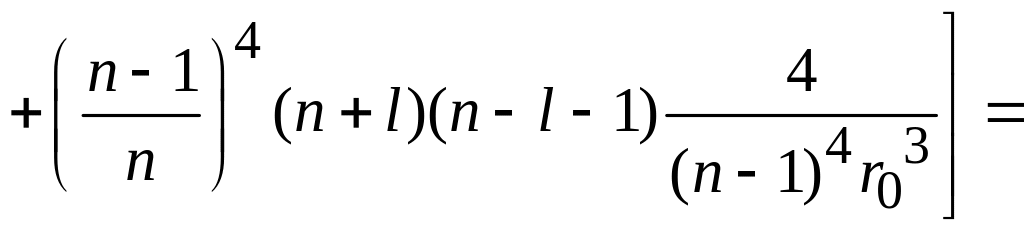
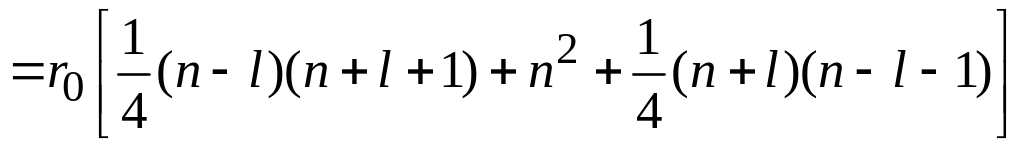Приведение подобных дает среднее расстояние электрона от ядра в состоянии

. (П.5.8)

2. Рекуррентное соотношение Крамерса связывает средние от расстояния электрона от ядра в разных степенях

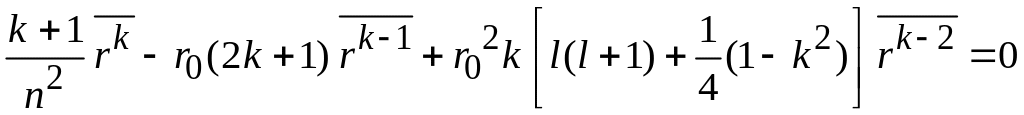, (П.5.10)

где

; .

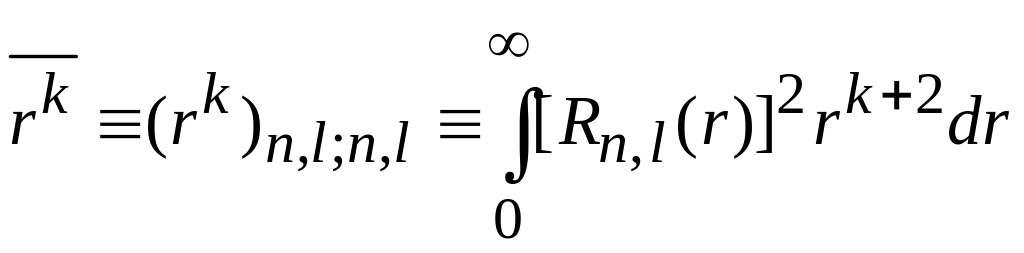Доказательство

• Интегрируем

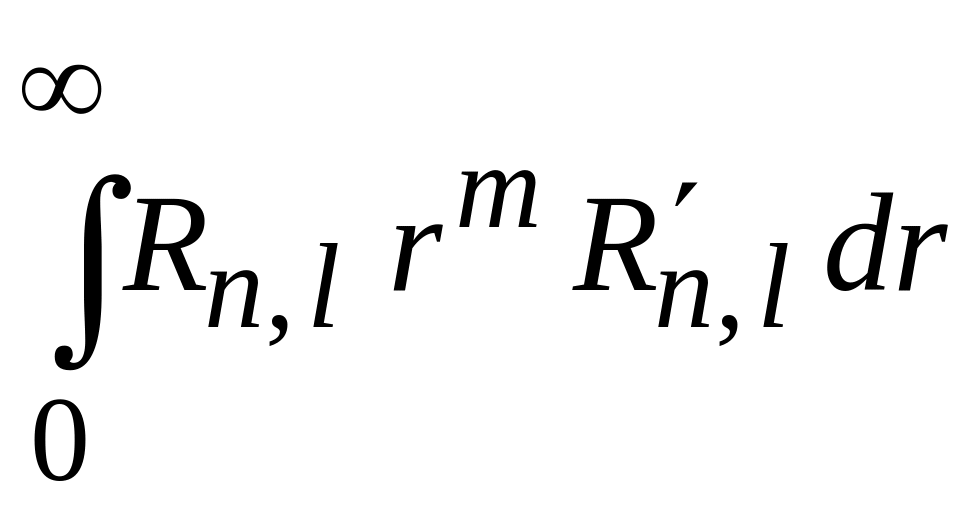
по частям, где

, .

Свободное слагаемое обращается в нуль, получаем

.

В результате

.

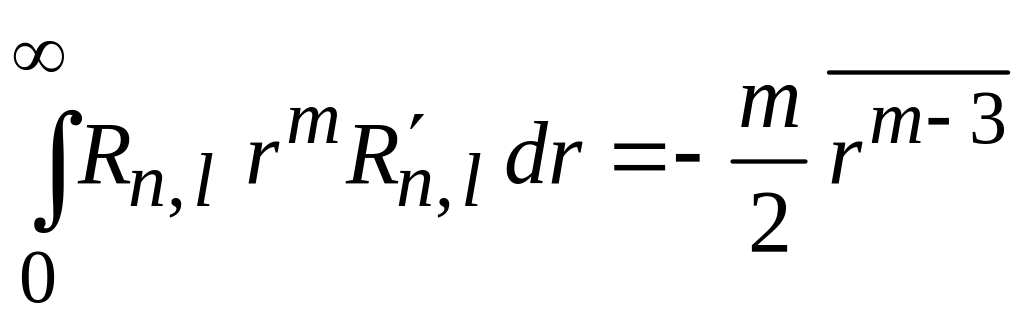• Интегрированием по частям аналогично находим

,

,

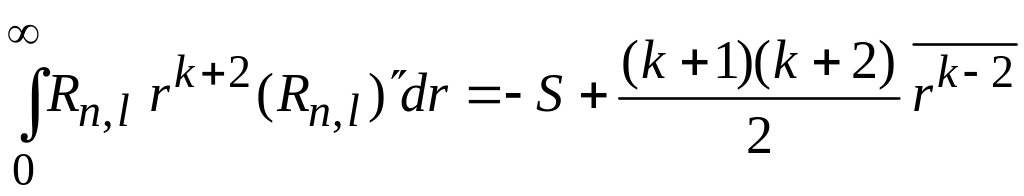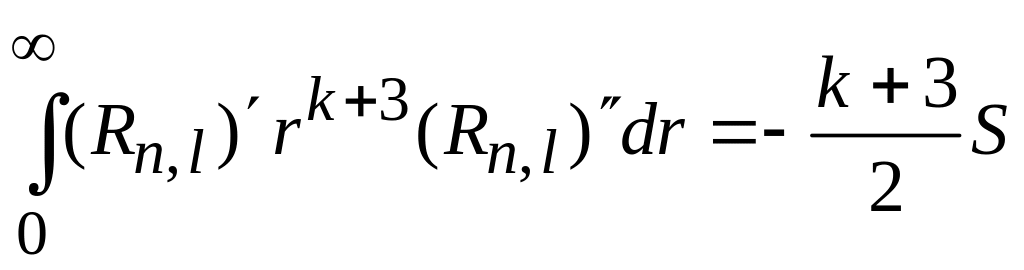где

.

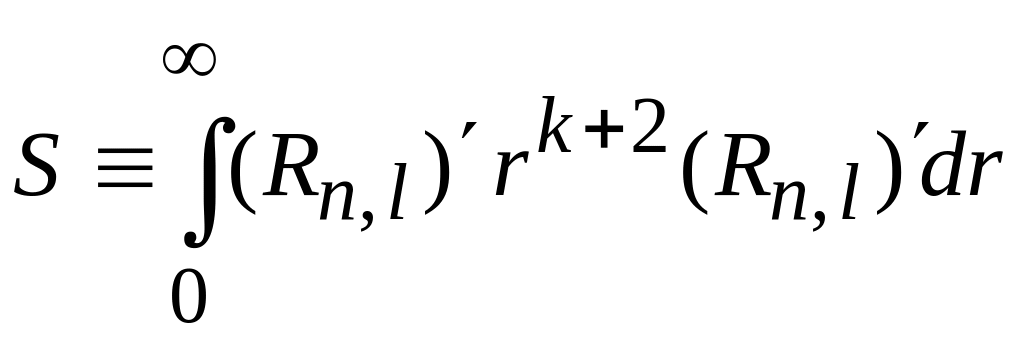• Используем уравнение Шредингера для радиальной функции (П.5.11)

.

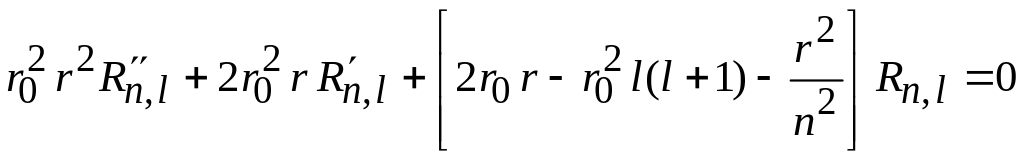Умножая уравнение на , интегрируем и получаем

.

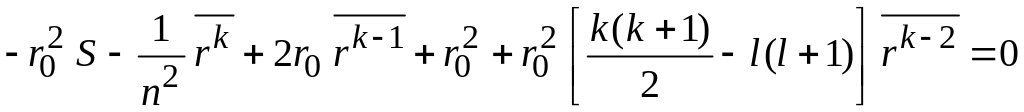Умножаем (П.5.11) на , интегрируем и находим

.

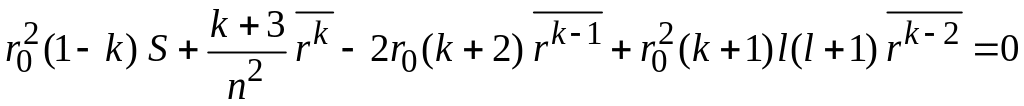• Исключая S из уравнений, получаем соотношение Крамерса (П.5.10).

Частные случаи

1. При из (П.5.10)

,

находим

,

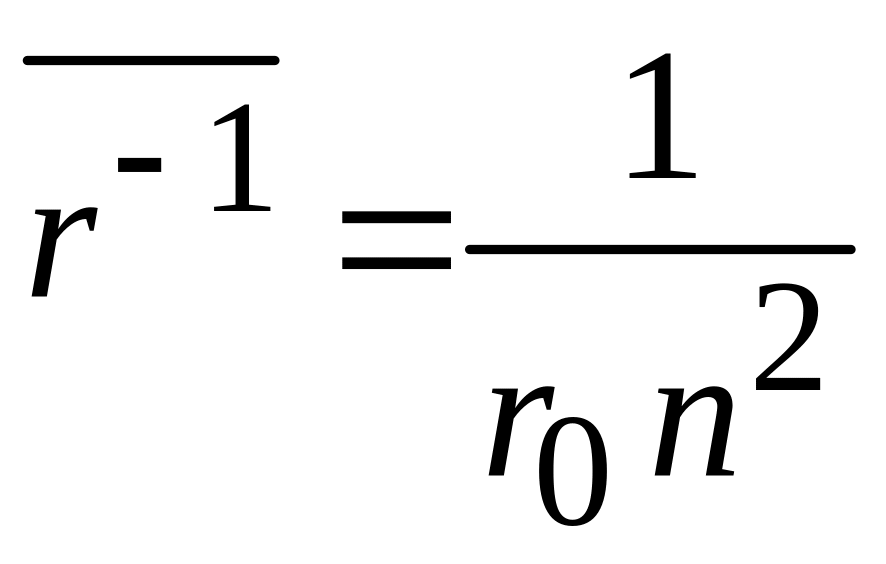. (П.5.11а)

С учетом (П.5.11а) и

, ,

получаем теорему вириала (от лат. сила)

.

Теорема выражает среднее значение потенциальной энергии через полную энергию Е.

2. При с учетом (П.5.11а) получаем

.

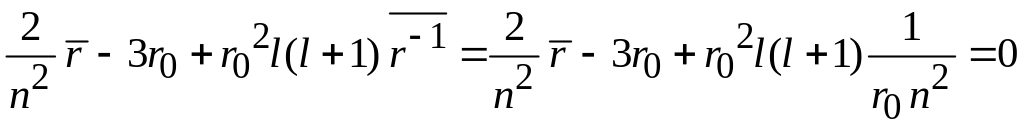Выражаем среднее расстояние, и находим (П.5.8)

. (П.5.11б)

3. При находим

. (П.5.11в)

Соотношение (П.5.10) не позволяет найти .

Полиномы Лежандра

, ; ; ;

– описывают угловую зависимость в полярных и сферических координатах;

– входят в собственные функции оператора момента импульса и оператора Лапласа;

– множество образует ортонормированный базис на интервале .

Полиномы исследовал Лежандр в 1785 г. Обозначены по первой букве англ. polynomial – полином.

Андре Мари Лежандр (1752–1833)

Уравнение Лежандра

, (6.93)

Используем

,

тогда

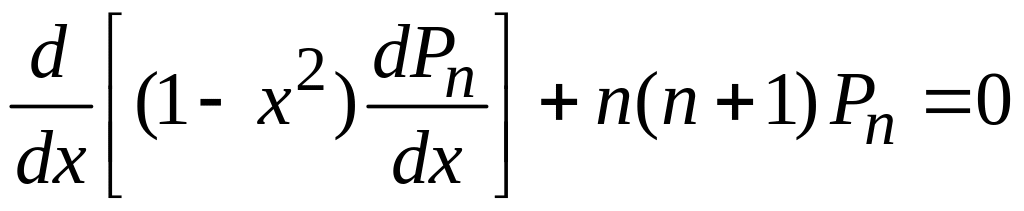. (6.93а)

С учетом области определения вводим угловую переменную

, ,

, ,

из (6.93а) для получаем

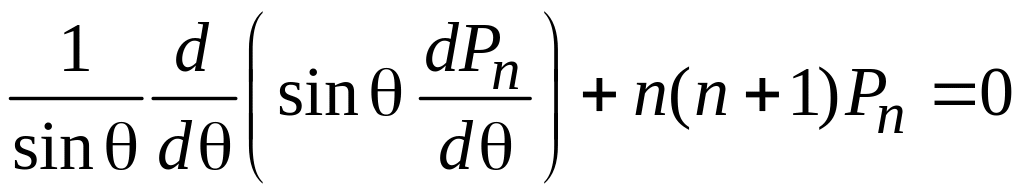. (6.94)

Решение уравнения методом факторизации

1. Уравнение (6.93)

относится к гипергеометрическому типу

.

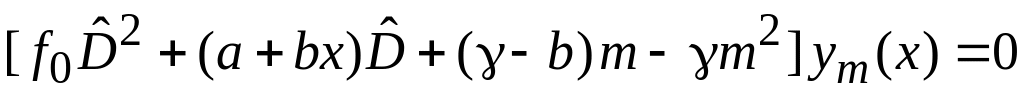2. Сравнение дает

,

, , , ,

, ,

,

,

, ,

,

.

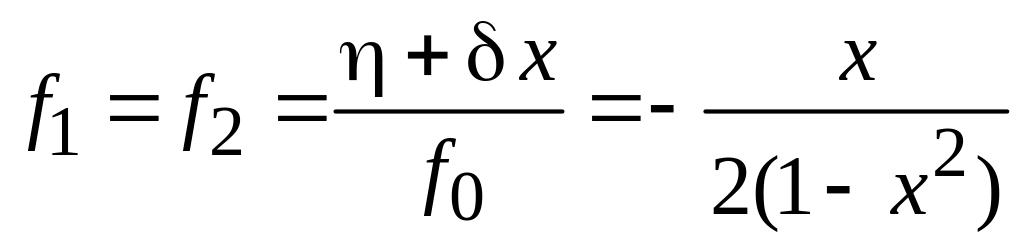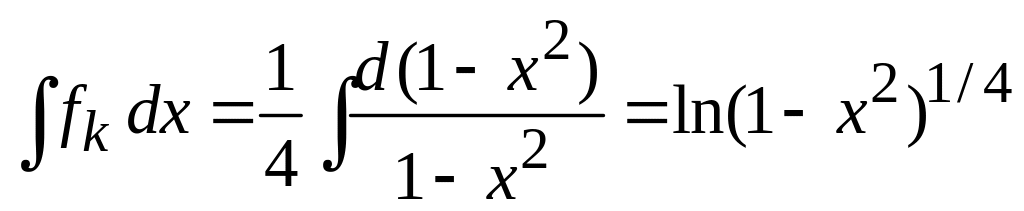3. Граничные условия

в виде

дают область определения

, .

4. Весовая функция

,

.

5. Решение Родрига

дает

.

Полагаем

,

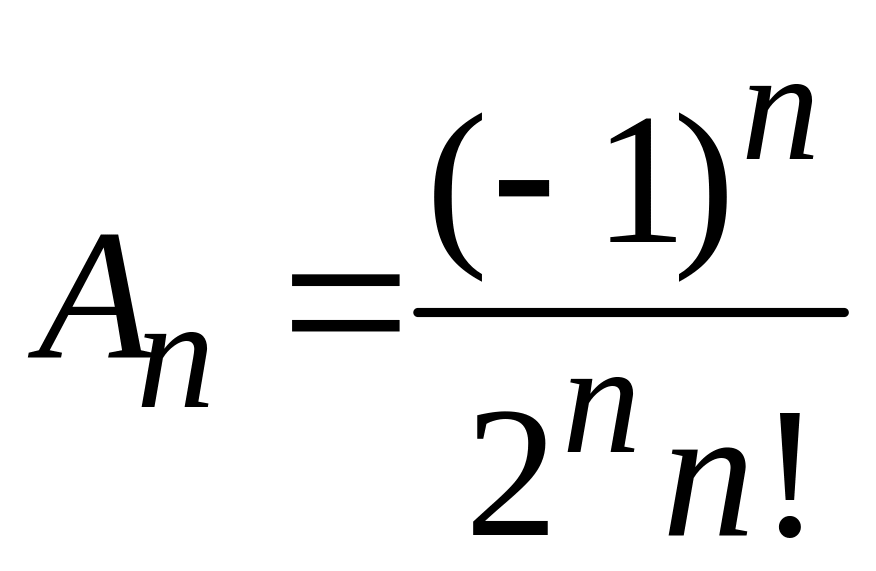получаем форму Родрига для полинома Лежандра

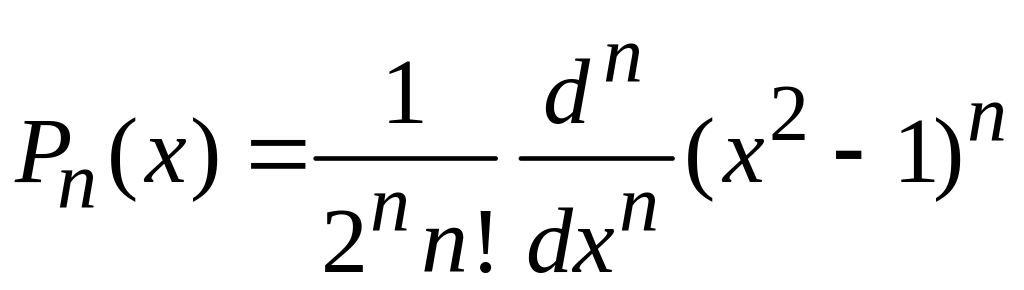. (6.96)

Свойство четности

, (6.97)

тогда

, n – нечетное.

6. Ортонормированность

, .

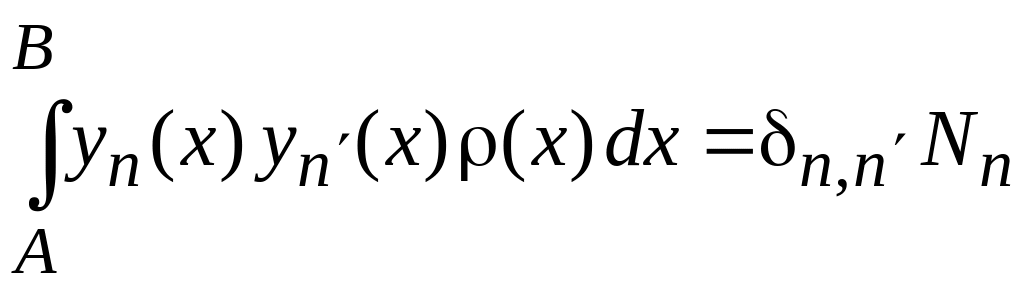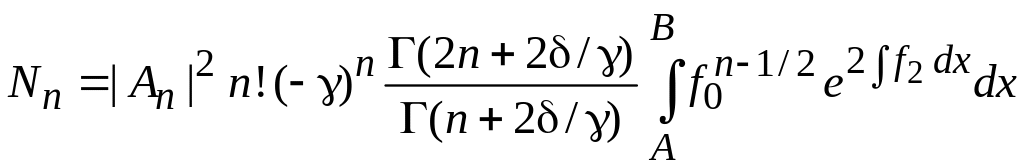Учитываем

, , ,

, , ,

,

,

,

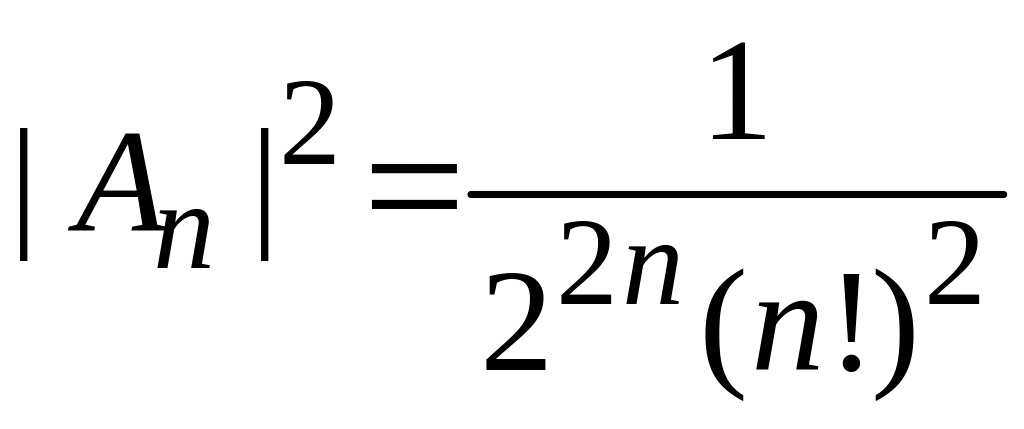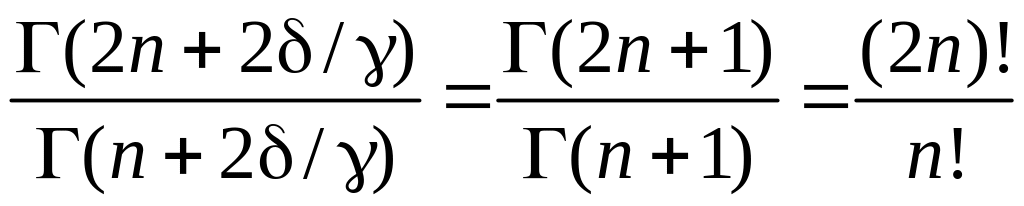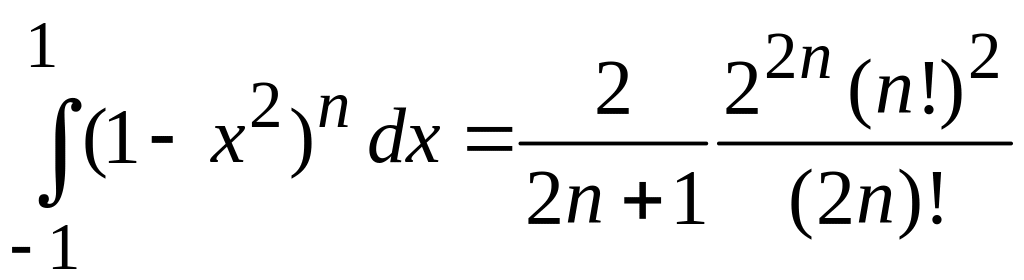где использовано (П.2.3)

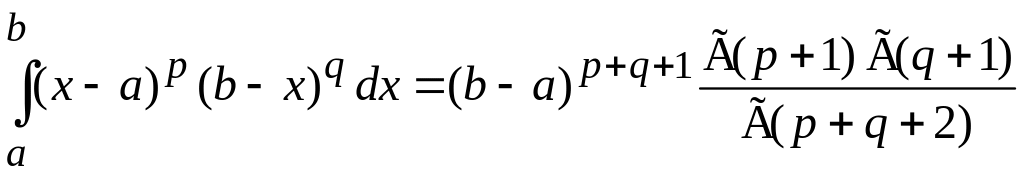
при , , . Получаем условие ортонормированности

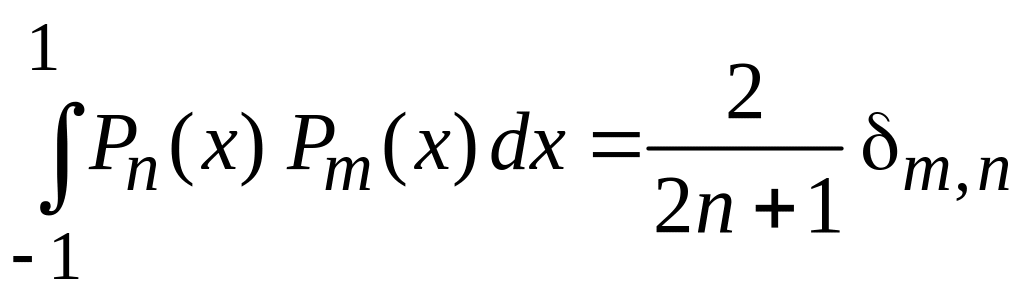. (6.112)

7. Производящая функция

,

с учетом

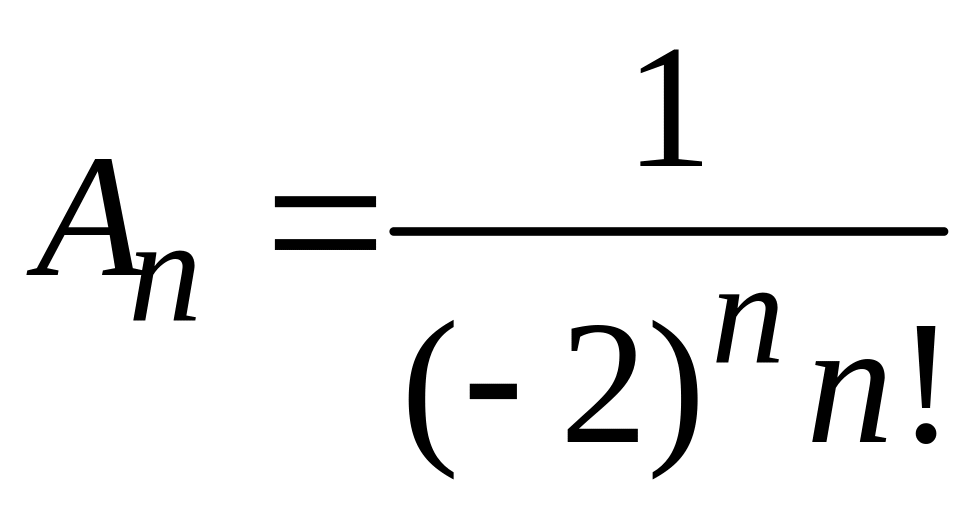
получает вид

.

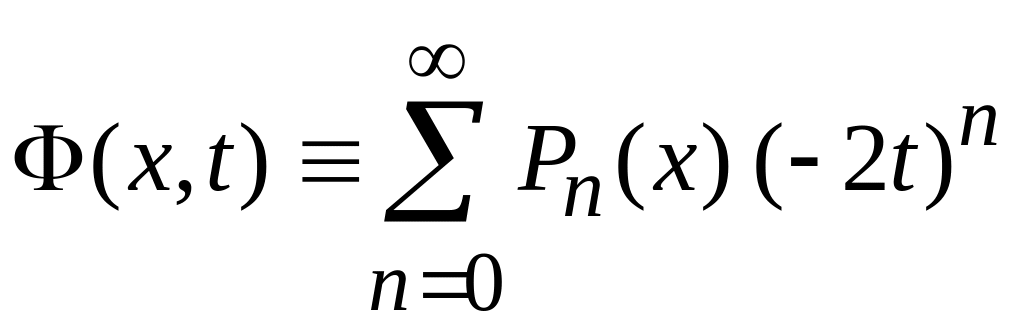Уравнение для ξ

, ,

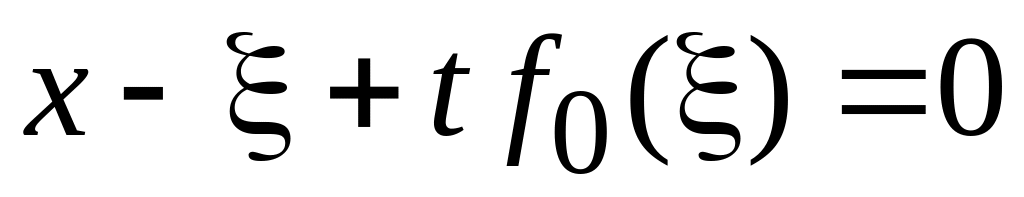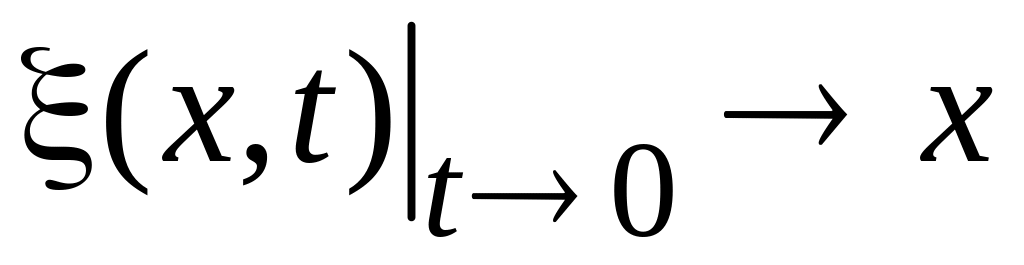где имеет вид

.

Находим решение

,

где выбор знака + обеспечивает требуемое поведение при

.

Использовано

, .

Из

,

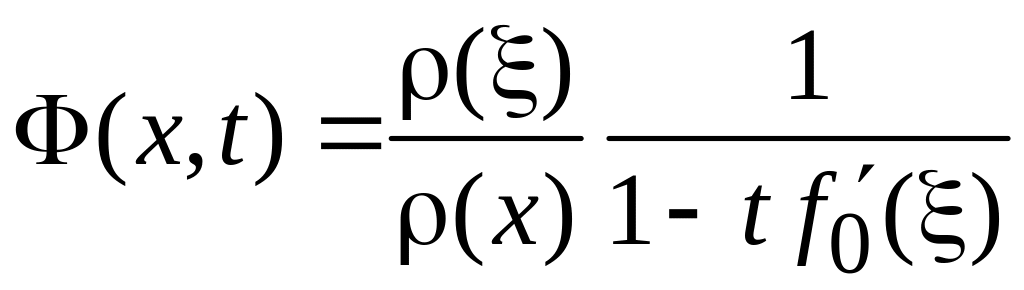с учетом

,

получаем

.

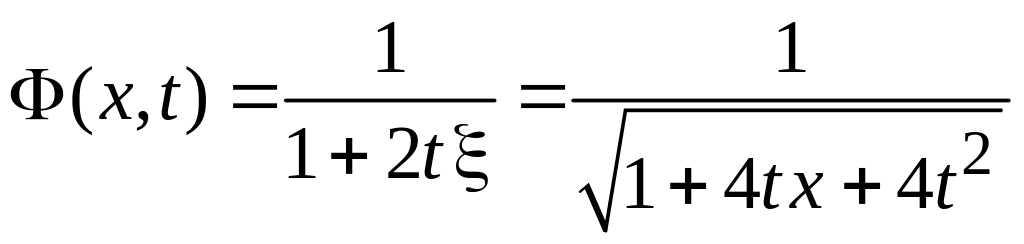Заменяем , тогда

, (6.101)

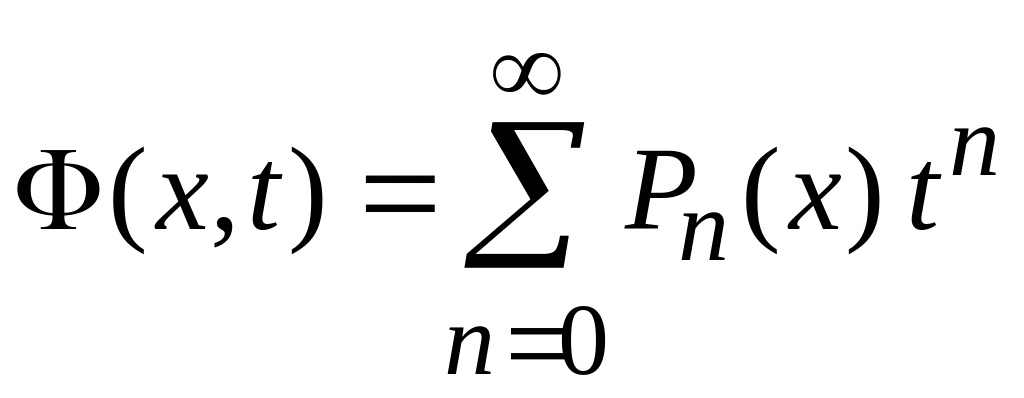. (6.102)