V2: Поле направлений и изоклины.
I:
21
S:
Уравнения семейства изоклин
дифференциального уравнения
имеют вид …
-:
-:
-:
+:
I:
S: Семейство интегральных кривых дифференциального уравнения
задаѐтся уравнениями вида…
+:
-:
-:
-:
I:
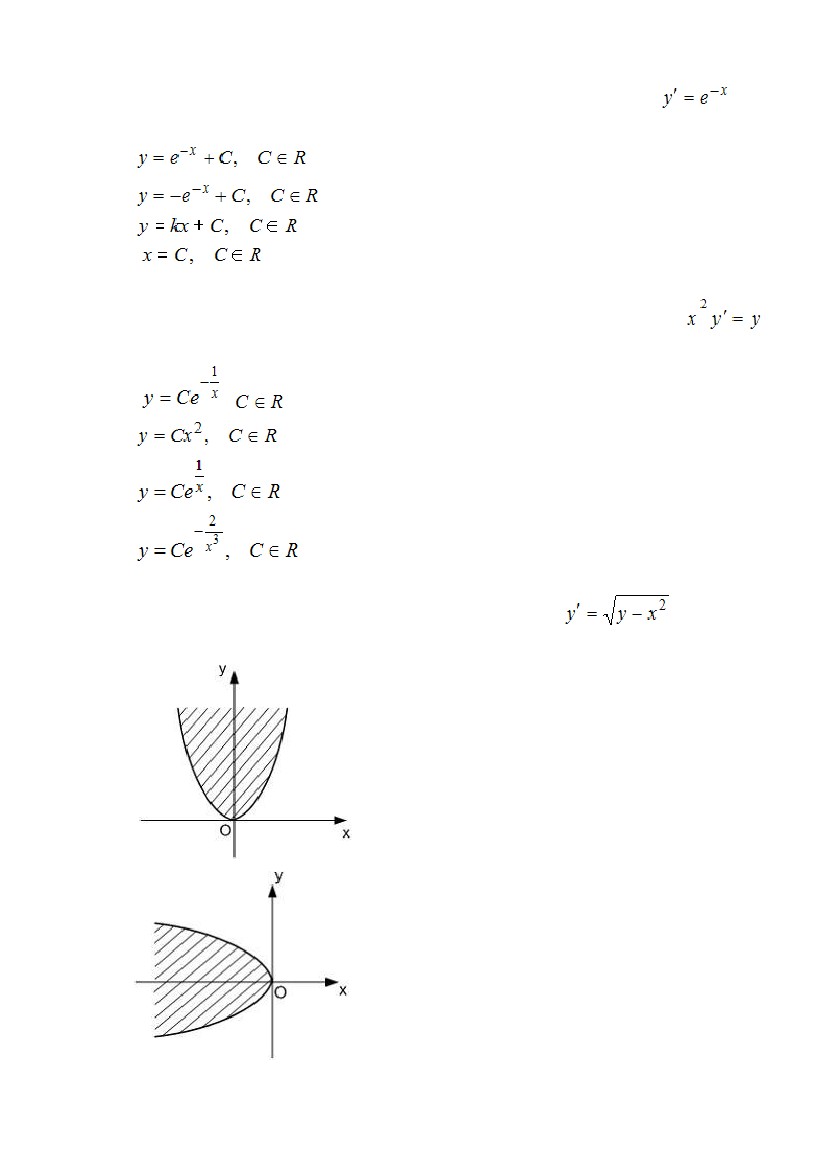
S: Поле направлений дифференциального уравнения
заштрихованную область координатной плоскости …
занимает
,
+:
-:
22
-:
-:
I:
S: Если задача Коши для дифференциального уравнения имеет вид,
у(1) = 1, то интегральная кривая, определяющая ее решение, имеет вид …
-: В
+: С
-: D
-: A
I:
23
S:
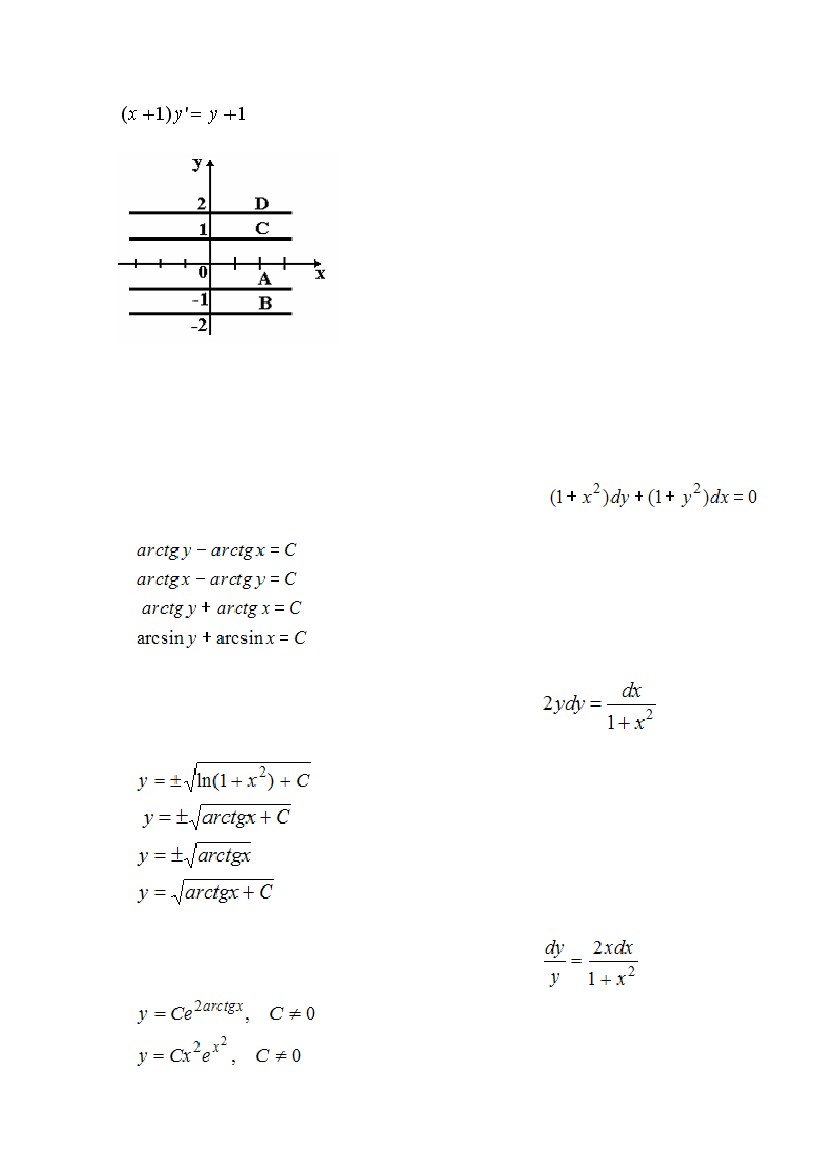
Если задача Коши для дифференциального
уравнения имеет вид
, у(0) = –1, то интегральная кривая, определяющая ее
решение, имеет вид …
-: B
-: C
+: A
-: D
V2: Дифференциальные уравнения с разделяющимися переменными.
I:
S: Общий интеграл дифференциального уравнения
имеет вид …
-:
-:
+:
-:
I:
S: Общее решение дифференциального уравнения
…
-:
+:
-:
-:
I:
S: Общее решение дифференциального уравнения
-:
-:
24
имеет вид …
имеет вид
-:
+:
I:
S: Общее решение дифференциального уравнения
имеет вид …
-:
-:
-:
+:
I:
,
,
,
,
при
S: Общий интеграл дифференциального уравнения
имеет вид…
-:
-:
+:
-:
I:
S: Общий интеграл дифференциального уравнения
имеет вид…
-:
-:
+:
,
25
-:
I:
S: Общее решение дифференциального уравнения
-:
-:
+:
-:
I:
S: Общее решение дифференциального уравнения
имеет вид …
-:
-:
-:
+:
I:
,
,
,
,
при
имеет вид
S: Общий интеграл дифференциального уравнения
имеет вид …
-:
-:
-:
+:
I:
S: Общий интеграл дифференциального уравнения
имеет вид …
-:,
26
+:
-:
-:
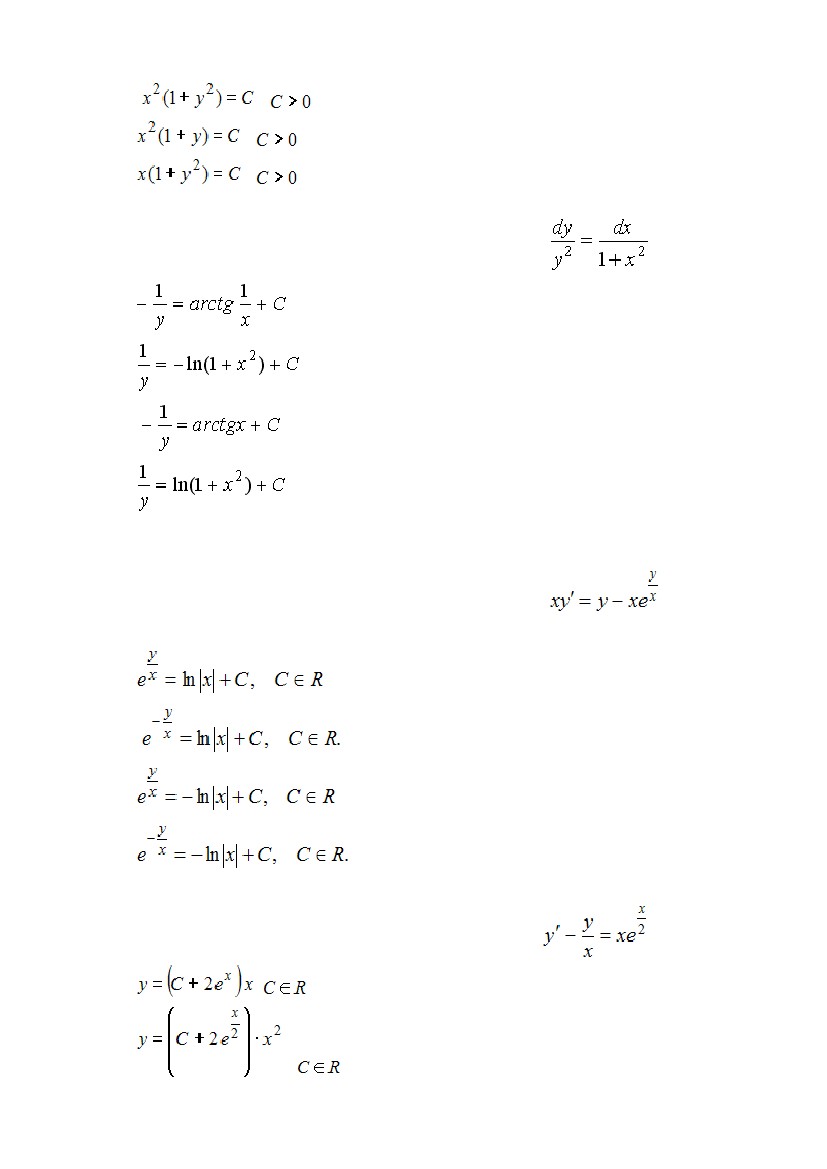I:
,
,
,
S: Общий интеграл дифференциального уравнения
-:
-:
+:
-:
V2: Однородные дифференциальные уравнения
I:
S: Общий интеграл дифференциального уравнения
…
-:
+:
-:
-:
I:
S: Общее решение дифференциального уравнения
-:
,
имеет вид…
имеет вид
имеет вид …
-:
,
27
+:
,
-:
I:
,
путѐм введения
S: Дифференциальное уравнение
новой неизвестной функцииприведено к уравнению с
разделяющимися переменными. Тогда полученное уравнение имеет вид …
-:
-:
-:
+:
I:
S: Частный интеграл дифференциального уравнения
начального условия
-:
-:
+:
-:
I:
S: Однородное дифференциальное уравнение первого порядка решается с
помощью замены:
-: x zy
28
имеет вид …
для
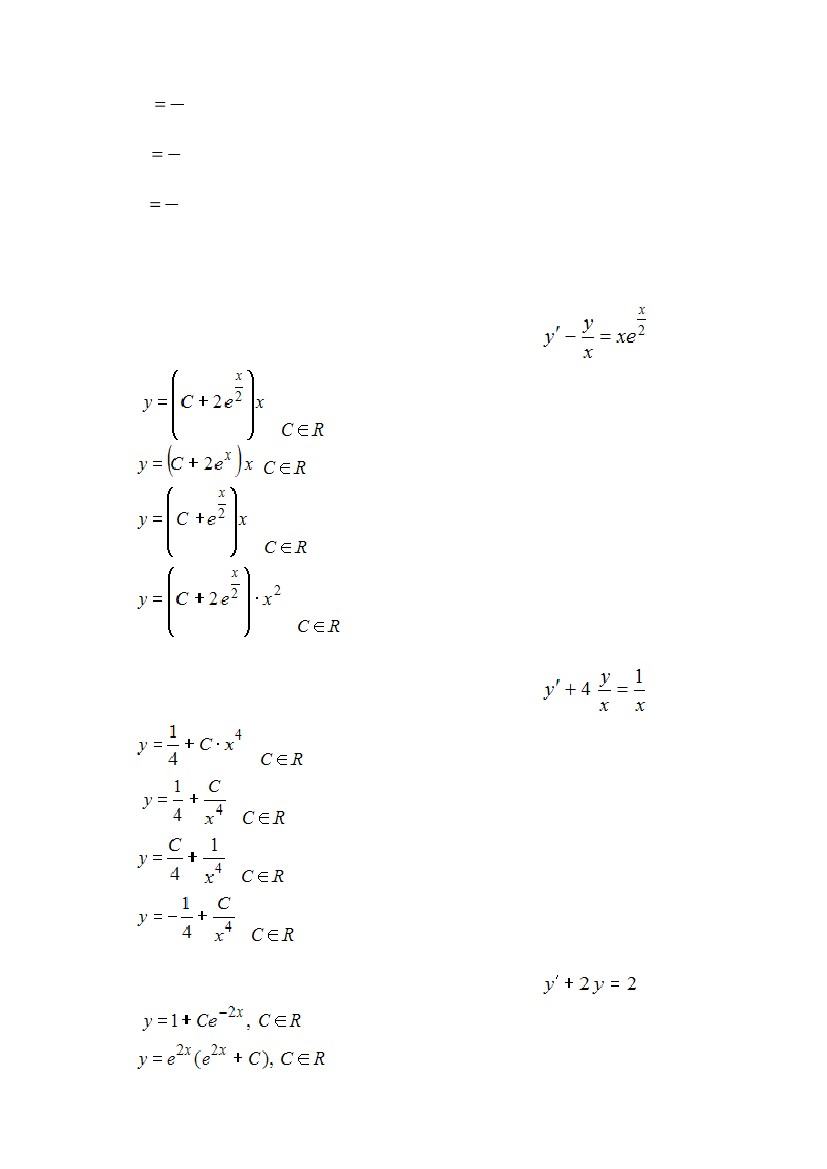y
x
z
-: y
x
x
-: z
y
V2: Линейные неоднородные дифференциальные уравнения первого
порядка.
I:
+: z
S: Общее решение дифференциального уравнения
имеет вид …
+:
-:
,
,
-:
,
-:
I:
,
S: Общее решение дифференциального уравнения
-:
+:
-:
,
,
,
имеет вид …
-:,
I:
S: Общее решение дифференциального уравнения
+:
-:
имеет вид …
29
-:
-:
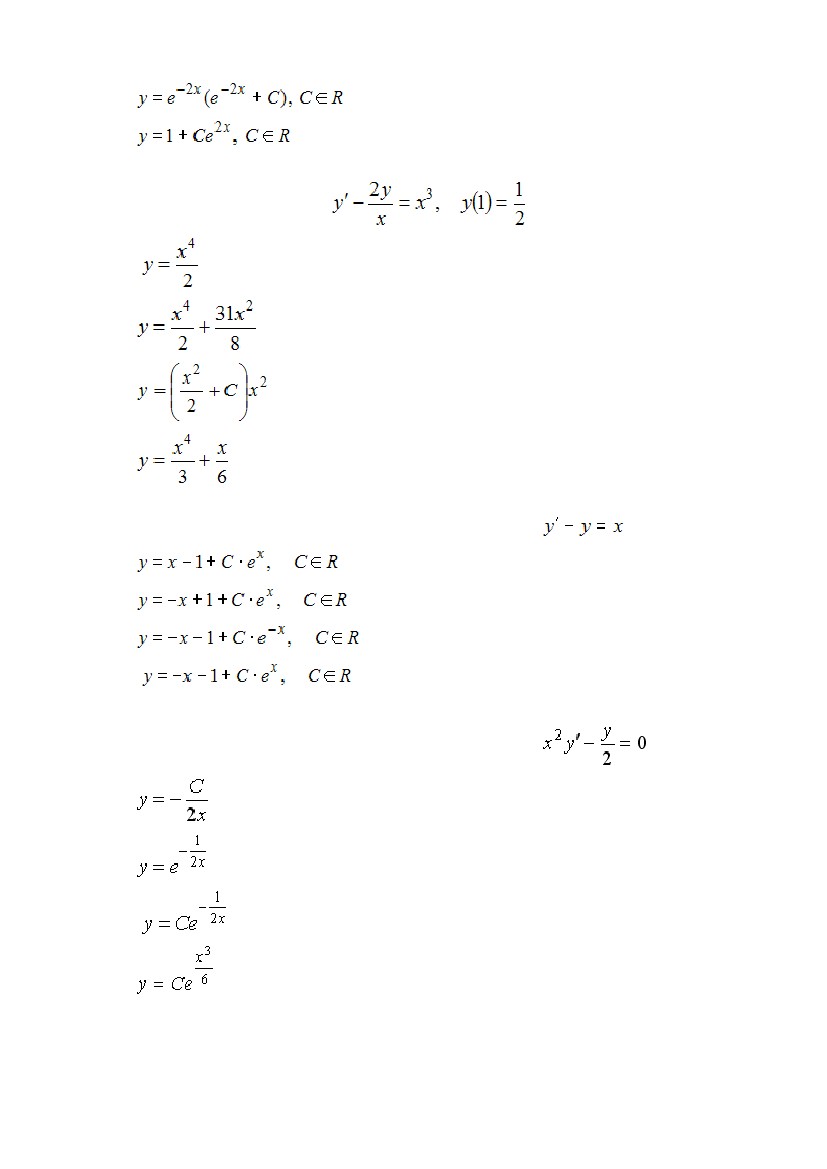I:
S: Решение задачи Коши
+:
-:
имеет вид …
-:
-:
I:
S: Общее решение дифференциального уравнения
-:
-:
-:
+:
I:
S: Общее решение дифференциального уравнения
-:
-:
+:
-:
I:
имеет вид
имеет вид …
30
S:
Общее решение дифференциального
уравнения
+:
-:
-:
-:
имеет вид
V2: Задача Коши для дифференциального уравнения первого порядка
I:
S: Частный интеграл дифференциального уравнения
для начального условия
+:
-:
-:
-:
I:
S: Решение задачи Коши
-:
-:
+:
-:
I:
S: Функцияявляется общим решением дифференциального
уравнения 1-го порядка. Тогда при начальном условиичастное
решение этого уравнения имеет вид…
-:
-:
31
имеет вид …
имеет вид …
-:
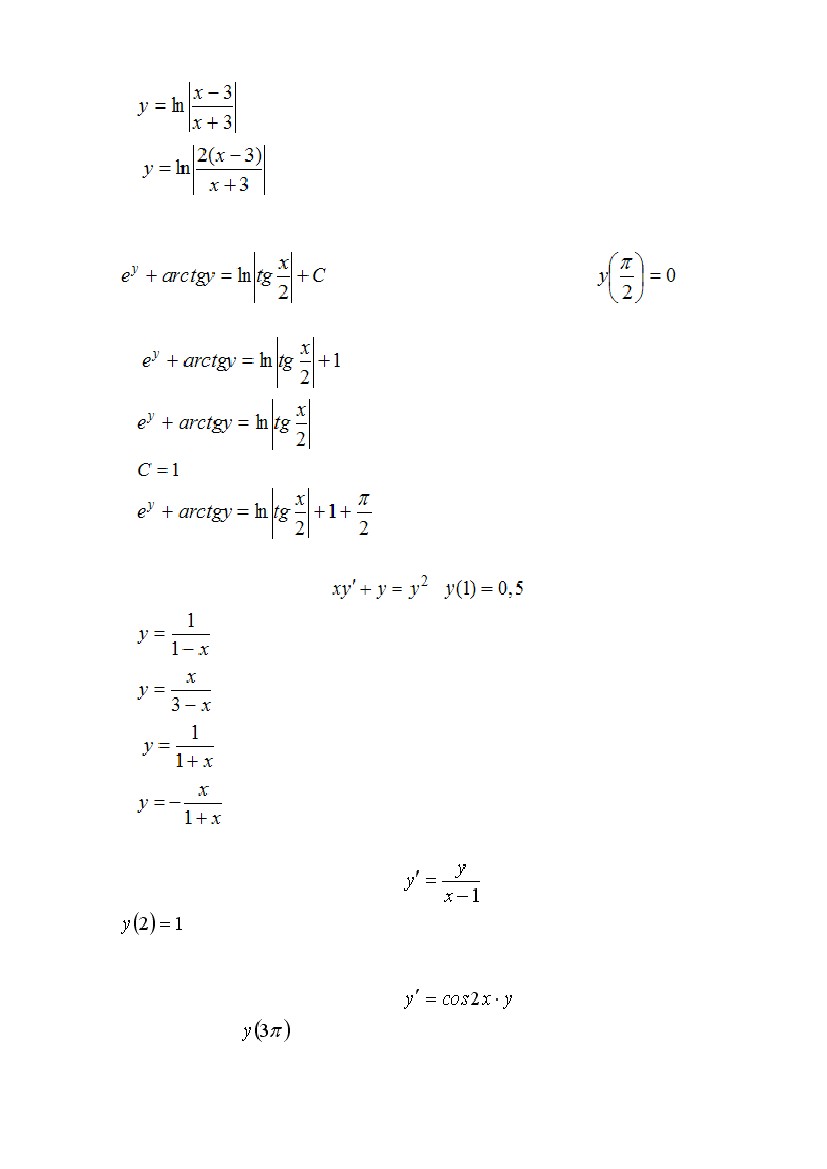+1
+:
I:
S: Общий интеграл дифференциального уравнения 1-го порядка имеет вид:
. Тогда при начальном условии
интеграл этого уравнения имеет вид …
+:
-:
-:
-:
I:
S: Решение задачи Коши
-:
-:
+:
-:
I:
S: Если у(х) – решение уравнения
, то у(1) равно …
+: 0
I:
S: Если у(х) – решение уравнения
у(0) = 1, тогда
+: 1
равно …
, удовлетворяющее условию
, удовлетворяющее условию
,
имеет вид…
частный
32
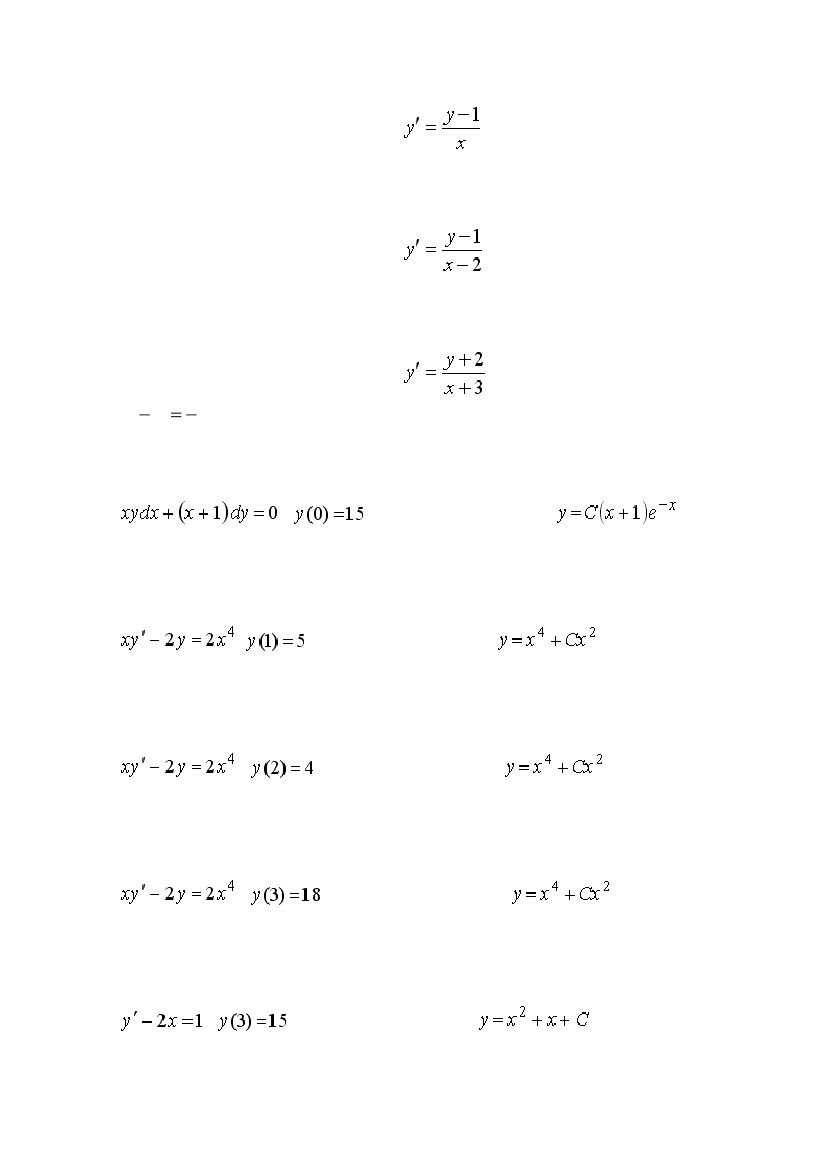I:
S: Если у(х) – решение уравнения
у(2) = 3, тогда у(1) равно …
+: 2
I:
S: Если у(х) – решение уравнения
у(1) = – 1, Тогда у(1,5) равно …
+: 2
I:
, удовлетворяющее условию
, удовлетворяющее условию
S: Если у(х) – решение уравнения, удовлетворяющее условию
y( 2)1, Тогда у(3) равно …
+: 4
I:
S: Если задача Коши для дифференциального уравнения имеет вид
,, то в общем решении
произвольная постоянная С равна …
+: 15
I:
S: Если задача Коши для дифференциального уравнения имеет вид
,, то в общем решениипроизвольная
постоянная С равна …
+: 4
I:
S: Если задача Коши для дифференциального уравнения имеет вид
,, то в общем решениипри произвольная
постоянная С равна …
+: -3
I:
S: Если задача Коши для дифференциального уравнения имеет вид
,, то в общем решениипроизвольная
постоянная С равна …
+: -7
I:
S: Если задача Коши для дифференциального уравнения имеет вид
,, то в общем решении
постоянная С равна …
+: 3
произвольная
33