АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ
«РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»
КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)
УТВЕРЖДАЮ
Проректор по учебной работе
Казанского кооперативного института
(филиала) Российского университета
кооперации
_____________Р. Х. Хайбрахманов
«____»_________________20___г.
МАТЕМАТИКА
ТЕСТОВЫЕ ЗАДАНИЯ
Направление подготовки (специальность) 222000.62 «Инноватика»
Составители:
________________________________ А.В. Поташев
________________________________ Е.В. Поташева
10 октября 2012 г.
Тестовые задания обсуждены на заседании кафедры «Инженерно-
технические дисциплины и сервис» 10 октября 2012 г., протокол № 3.
Заведующий кафедрой ___________________________ А.М. Мухаметшин
СОГЛАСОВАНО
Начальник отдела менеджмента качества _______________ Д.Н. Алюшева
1
№
1.
2.
3.
4.
5.
Наименование пункта
Кафедра
Автор – разработчик
Наименование дисциплины
Общая трудоемкость по
учебному плану
Вид контроля (нужное
подчеркнуть)
Для специальности(ей)/
направления(й) подготовки
Количество тестовых заданий
всего по дисциплине, из них
Количество заданий при
тестировании студента
Из них правильных ответов
(в %):
для оценки «отлично»
для оценки «хорошо»
для оценки
«удовлетворительно»
или для получения оценки
«зачет» не менее
Время тестирования (в
минутах)
Значение
Инженерно-технические
дисциплины и сервис
Поташев А.В., д.ф.-м.н., профессор
Поташева Е.В., к.т.н., доцент
Математика
144 (2 семестр )
Предварительный (входной),
текущий, промежуточный
(экзамен)
222000.62 «Инноватика»
нормативный срок
очная форма обучения
145
11
6.
7.
8.
9.
10.
11.
12.
85 % и больше
70 % - 85%
50% - 70%
-
45
13.
2
Содержание
Стр.
V1: ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ................................................................ 4
V2: Неопределенный интеграл .......................................................................... 4
V2: Определенный интеграл .............................................................................. 6
V2: Несобственные интегралы ........................................................................ 12
V1: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ .................................................... 15
V2: Тип дифференциального уравнения......................................................... 15
V2: Поле направлений и изоклины. ................................................................ 21
V2: Дифференциальные уравнения с разделяющимися переменными....... 24
V2: Однородные дифференциальные уравнения ........................................... 27
V2: Линейные неоднородные дифференциальные уравнения первого
порядка. .............................................................................................................. 29
V2: Задача Коши для дифференциального уравнения первого порядка ..... 31
V2: Линейные дифференциальные уравнения второго порядка с
постоянными коэффициентами ....................................................................... 34
V2: Дифференциальные уравнения высших порядков, допускающие
понижение порядка. .......................................................................................... 40
3
F1:
Математика экзамен 2 семестр 2012/2013
F2: Поташев А.В., Поташева Е.В.
F3: Тестовые задания по направлению подготовки 222000.62 «Инноватика»
очная нормативный срок 145 заданий, 11 вопросов, 144 часа
F4: Дидактическая единица; Раздел; Тема
V1: Интегральное исчисление
V2: Неопределенный интеграл
I:
S: Множество первообразных функцииописывается
соотношением …
-:
+:
-:
-:
I:
S: Первообразными функции
+:
-:
+:
-:
+:
I:
S: Первообразными функции
-:
+:
+:
-:
I:
4
являются…
являются …
S:
Первообразными функции
-:
+:
+:
-:
I:
S: Первообразными функции
-:
+:
+:
-:
I:
S: Первообразными функции
-:
+:
-:
+:
I:
S: Первообразными функции
+:
-:
-:
+:
I:
S: Первообразными функции
-:
+:
+:
-: 7 cos 7x
I:
являются…
являются…
являются…
являются…
являются…
5
S:
Первообразными функции
+:
-:
+:
-: 18cos9x
I:
S: Первообразными функции
+:
+:
-:
-: 84sin12x
I:
S: Первообразными функции
+:
+:
-:
-:
V2: Определенный интеграл
I:
являются…
являются…
являются…
S: Среднее значение функции y sin 2 x на отрезке 0;
-:
2
равно …
2
-: 1
2
+:
-:
2
I:
S: Среднее значение функции y
1
-:
2
x2 на отрезке 0;1 равно …
6
-:
1
1
+:
3
1
-:
3
I:
S: Среднее значение функции y sin 2 x на отрезке
-:
2 2
;
равно …
2
+: 0
2
-:
-:
I:
S: Среднее значение функции y cos5x на отрезке 0;
-:
5
2
равно …
5
-: 1
5
-:
+: 0
I:
S: Среднее значение функции y cos5x на отрезке
-:
;равно …
10 10
5
-: 0
2
+:
-:
I:
5
S: Определенный интеграл
+: – 0.5
-: 0.5
-: 0
равен …
7
-:
– 2
I:
S: Определенный интеграл
-:
+:
-:
-:
I:
2
равен…
S: Определенный интеграл
1
3x3 2 xe x
x
4 x2
dx равен…
-: 2e2 2e 13
+: 2e2 2e 13
-: 2e 2e2 13
-: 2e2 2e 14
I:
S: Объем тела, образованного вращением вокруг оси Ox фигуры,
ограниченной параболой y x2 1 и осью Ox , равен …
-:
16
+:
15
2
-:
3
-:
2
I:
S: Объем тела, образованного вращением вокруг оси Ox фигуры,
ограниченной параболами y x2 и yx , равен …
-:
16
-:
15
9
-:
70
3
+:
10
I:
8
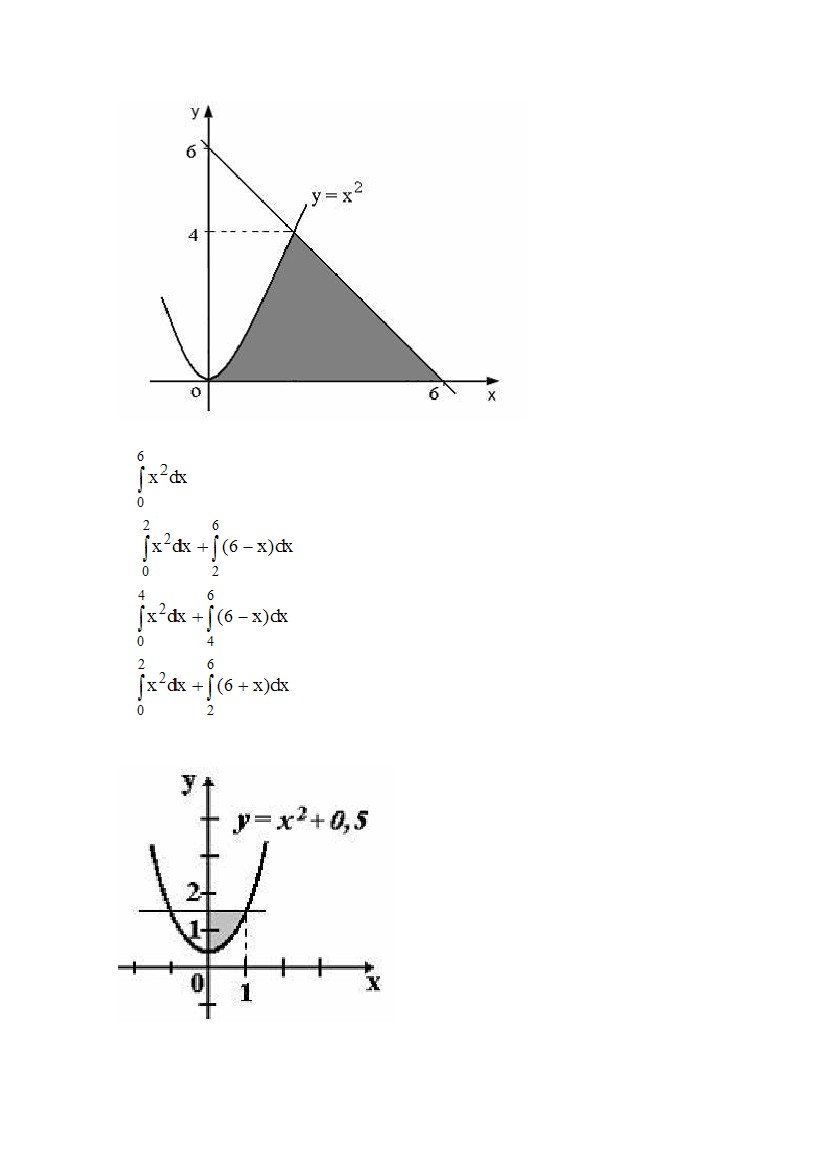S:
Площадь фигуры, изображенной на рисунке,
может быть вычислена как …
-:
+:
-:
-:
I:
S: Площадь фигуры, изображенной на рисунке,
может быть вычислена как …
9
-:
-:
+:
-:
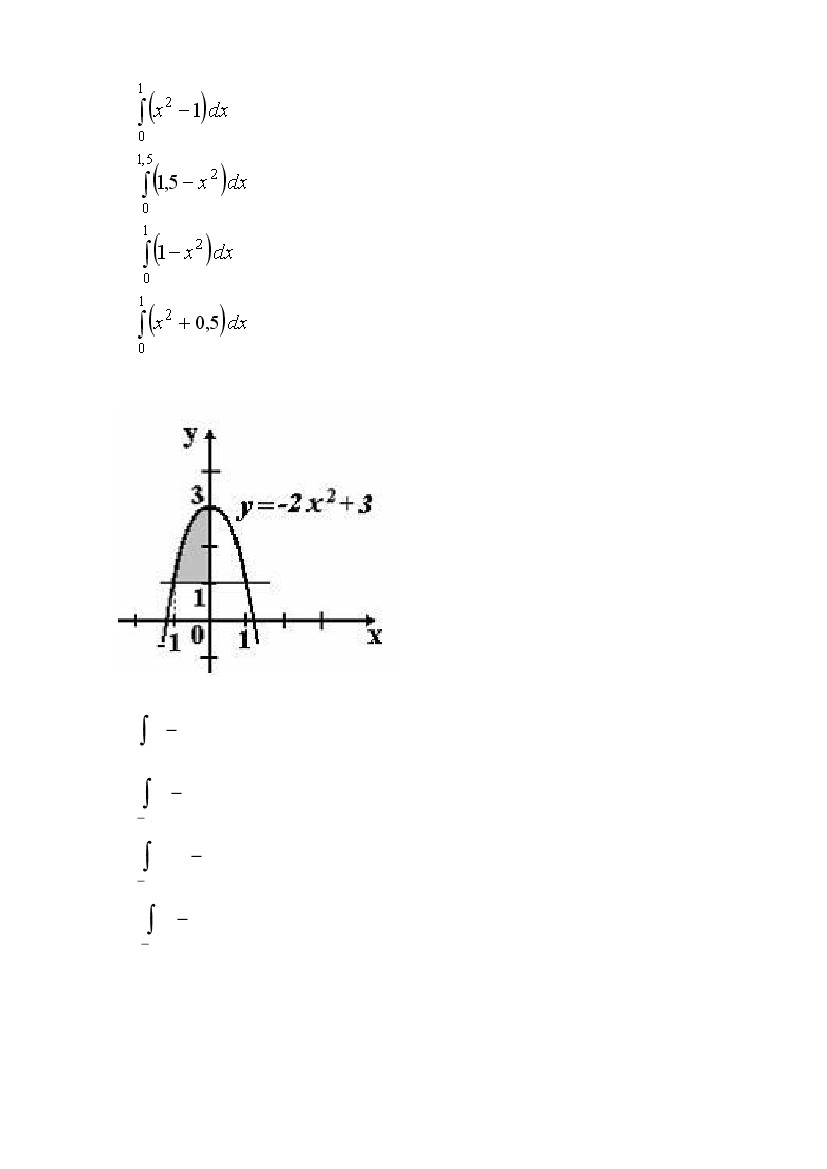
I:
S: Площадь фигуры, изображенной на рисунке,
может быть вычислена как …
3
-: (3 2 x 2 )dx
0
0
-:
1
0
(3 2 x 2 )dx
-:
1
0
(2 x 2 2)dx
(2 2 x 2 )dx
1
+:
I:
10
S:
Площадь фигуры, изображенной на рисунке,
может быть вычислена как …
-:
-:
-:
+:
I:
S: Площадь фигуры, ограниченной линиями,
вычисляется с помощью определенного интеграла…
-:
-:
-:
+:
I:
,
,
11
S:
Площадь фигуры, ограниченной линиями,
вычисляется с помощью определенного интеграла…
-:
+:
-:
-:
V2: Несобственные интегралы
I:
S: Несобственный интеграл обозначается:
b
,
,
-:
a
f ( x)dx
+:
a
b
f ( x)dx
f ( x)dx
0
+:
-:
a
f ( x)dx
+:
f ( x)dx
I:
S: Несобственным интегралом называется:
b
-: lim f ( x )dx
x
a
R
+: lim
R
a
f ( x)dx
b
+: lim
R
R
x
f ( x)dx
-: lim f (t )dt
t
a
12
I:
S: Несобственный интеграл
+: 0.5
-:
-: -0.5
-: 4
I:
S: Несобственный интеграл
+: 0.25
-: - 0.25
-:
-: 8
I:
S: Несобственный интеграл
-: 4
-:
+:
-:
I:
S: Сходящимися являются несобственные интегралы …
-:
+:
-:
+:
I:
равен …
равен …
равен …
13
S:
Сходящимися являются несобственные
интегралы …
-:
+:
-:
+:
I:
S: Сходящимися являются несобственные интегралы …
-:
-:
+:
+:
I:
S: Сходящимися являются несобственные интегралы …
+:
-:
-:
+:
I:
S: Сходящимися являются несобственные интегралы …
-:
14
-:
+:
+: