
- •1.Теориялық механика пәнінің зерттейтін негізгі мәселелері мен тәсілдері
- •2. Кеңістікте берілген нүктенің орнын анықтау тәсілдері.
- •3.Жалпылама координаттар. Координаттық беттер, сызықтар. Ламэ коэффициенттері.
- •4. Жалпылама жылдамдық. Координаттардың ортогональды жүйесі
- •5.Қисықсызықты қозғалыс жылдамдығы
- •6.Жылдамдықтың радиал және трансверсаль құраушылары
- •7.Нүкте жылдамдығының қисықсызықты координаттарда жазылуы
- •8. Механиканың заңдары. Галилейдің салыстырмалық принципі. Инерциалды санақ жүйелері.
- •9. Механиканың детерминизмі. Ньютонның қозғалыс теңдеулері
- •10. Бірінші, екінші қозғалыс интегралдары
- •11.Еркін материалдық нүктенің Лагранж функциясы. Материалдық бөлшектер жүйесінің Лагранж функциясы
- •12. Ең аз әсер принципі немесе Гамильтон принципі
- •13. Лагранж теңдеулерін механиканың ең аз әсер принципінен қорытып шығару
- •14.Гамильтон функциясы. Оның физикалық мағынасы
- •15. Гамильтонның ең аз әсер принципінен оның канондық теңдеулер жүйесін қорытып шығару
- •16. Импульстің, импульс моментінің, энергияның сақталу заңдарының кеңістік пен уақыт симметрияларымен байланысы. Энергияның сақталу заңы
- •17. Сақталу заңдарының кеңістік пен уақыт симметрияларымен байланысы. Импульстің сақталу заңы
- •18. Сақталу заңдарының кеңістік пен уақыт симметрияларымен байланысы. Импульс моменті сақталу заңы
- •19. Инерция центрі
- •21. Бір өлшемді қозғалыс
- •22.Орталық өрістегі қозғалыс
- •23. Аудандар заңы немесе Кеплердің екінші заңы
- •24. Кеплердің бірінші және үшінші заңдары
- •27. Бөлшектердің ыдырау энергиясы
- •28. Бөлшектердің ыдырау жылдамдығын шарты бойынша қарастыру
- •29. Бөлшектердің ыдырау жылдамдығын шарты бойынша қарастыру
- •30.Бөлшектердің серпімді соқтығысы
- •1.Бөлшектердің шашырауы. Шашыраудың эффективті қимасы
- •2.Бөлшектердің шашырауының эффективті қимасына арналған Резерфорд формуласы
- •3. Аз тербелістер. Бір өлшемді еркін тербелістер
- •4.Гармониялық тербелістер
- •5.Еріксіз тербелістер
- •6. Периодты гармониялық күштің әсерінен болатын еріксіз тербелістер
- •7. Резонанс кезіндегі тербеліс амплитудасы және энергиясы
- •8.Өшетін тербелістер. Өшу коэффициенті
- •9.Үйкеліс күші бар кездегі еріксіз тербелістер
- •10. Үйкеліс күші бар кездегі еріксіз тербелістердің амплитудасы
- •11. Еріксіз тербелістердің фазасы
- •12.Ангармониялық тербелістер
- •13.Абсолют қатты дене. Оның еркіндік дәрежелері. Абсолют қатты дененің координаттары. Эйлер бұрыштары
- •14. Бұрыштық жылдамдық. Бұрыштық жылдамдықтың қозғалыстағы санақ жүйесінің остеріне проекциялары. Лездік айналу осі
- •15.Абсолютті қатты дененің инерция тензоры. Инерцияның бас өстері
- •16. Инерция моменттері бас осьтері. Ассиметриялы ұршық
- •17. Инерция моменттері бас осьтері. Симметриялы ұршық
- •18. Инерция моменттері бас осьтері. Сызықтық ұршық
- •19.Қатты дененің импульс моменті
- •20.Қатты дененің қозғалыс теңдеулері
- •21. Күш моменті
- •22. Бір нүктесі бекітілген абсолютті қатты дене үшін Эйлердің қозғалыс теңдеулері
- •23.Инерциалды емес санақ жүйелеріндегі қозғалыс
- •24. Инерциалды емес санақ жүйелеріндегі денелердің айналмалы қозғалысы теңдеуі
- •25. Инерциалды емес санақ жүйелеріндегі толық энергия
- •26. Пуассон жақшалары. Пуассон жақшаларының қасиеттері
- •27. Якоби теңдігі
- •28. Гамильтон-Якоби теңдеуі
- •29. Гамильтон-Якоби теңдеуі математикалық құрылысы. Толық интегралы
- •30.Айнымалыларды ажырату тәсілі
27. Бөлшектердің ыдырау энергиясы
Тоқтап
тұрған кезде механикалық энергия
![]() ,
ал ыдырағанда:
,
ал ыдырағанда:
![]() (1)
(1)
![]()
![]() (2)
(2)
Ал
ыдырау энергиясы – бастапқы бөлшектің
ішкі энергиясының
![]() ,
кейіннен пайда болған екі бөлшектің
ішкі энергияларының айырмалары:
,
кейіннен пайда болған екі бөлшектің
ішкі энергияларының айырмалары:
![]() (3)
(3)
Энергияны импульс арқылы жазамыз:
 (4)
(4)
![]() екенін
ескерсек,
екенін
ескерсек,
![]()
![]() (5)
(5)
![]() (6)
(6)
Енді жылдамдықты жазамыз. Яғни ыдыраған кезде бөлшек импульстері бірдей болғанымен жылдамдықтары әртүрлі болады (тыныштықтағы с.ж. )
![]()
![]() (7)
(7)
28. Бөлшектердің ыдырау жылдамдығын шарты бойынша қарастыру
Бөлшек
ыдырауға дейін
жылдамдықпен қозғалсын, яғни лабораториялық
санақ жүйесінде (л.с.ж.), ал массалар
центрі санақ жүйесіндегі жылдамдығы –
![]() және
және
![]() .
.
Ыдыраған бөлшектердің тек біреуін ғана қарастырайық. Галилей түрлендірулері арқылы:
![]() немесе
немесе
![]() (1)
(1)
![]() (2)
(2)
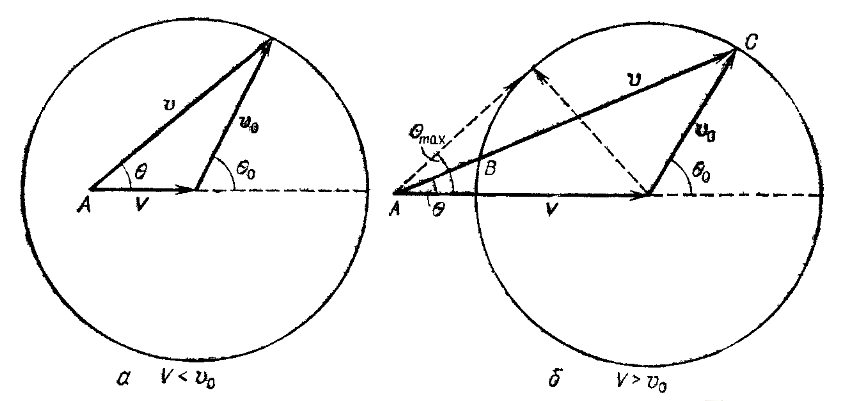
а)
![]() б)
б)
![]()
1– сурет
![]() болғандағы
жағдайды қарастыралық.
болғандағы
жағдайды қарастыралық.
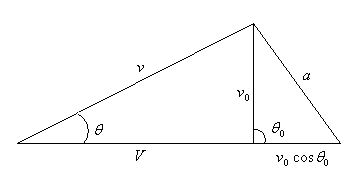
2 – сурет
![]() -
л.с.ж. ұшып шығу бұрышы,
-
л.с.ж. ұшып шығу бұрышы,
![]() - и.ц.с.ж. ұшып шығу бұрышы. Ал екеуінің
байланысы:
- и.ц.с.ж. ұшып шығу бұрышы. Ал екеуінің
байланысы:
![]() (3)
(3)
суреттен
![]()
![]() (4)
(4)
![]()
![]() (5)
(5)
29. Бөлшектердің ыдырау жылдамдығын шарты бойынша қарастыру
Бөлшек ыдырауға дейін жылдамдықпен қозғалсын, яғни лабораториялық санақ жүйесінде (л.с.ж.), ал массалар центрі санақ жүйесіндегі жылдамдығы – және .
Ыдыраған бөлшектердің тек біреуін ғана қарастырайық. Галилей түрлендірулері арқылы:
немесе (1)
(2)
а) б)
1– сурет
![]() болғанда,
бөлшек алға қарай ұшып шығады.
болғанда,
бөлшек алға қарай ұшып шығады.
![]() бұрышы
бұрышы
![]() -нан
үлкен болмайды.
-нан
үлкен болмайды.

1 – сурет
![]()
![]()
![]() (1)
(1)
шешеміз:
![]()
![]()
 (2)
(2)
![]() болғанда
және
арасындағы байланыс бір мәнді болып
келеді. (2) формуладағы түбірдің таңбасын
«+» деп аламыз (
=0
=0).
болғанда
және
арасындағы байланыс бір мәнді болып
келеді. (2) формуладағы түбірдің таңбасын
«+» деп аламыз (
=0
=0).
Егер
![]() болса
болса
![]() және
арасындағы байланыс бір мәнді бола
алмайды.
-ның
әрбір мәніне
екі мәні сәйкес келеді де,
және
арасындағы байланыс бір мәнді бола
алмайды.
-ның
әрбір мәніне
екі мәні сәйкес келеді де,
![]() векторының таңбасы түбір алдындағы
векторының таңбасы түбір алдындағы
![]() екеуі де болады. Негізінде физикада
осындай ыдырауларды тек бір ғана бөлшек
үшін емес, көптеген бірдей бөлшектер
үшін қарастыру керек. Сондықтан ыдыраған
бөлшектердің бағыттарын, энергияларын
қарастыру қажет болады. Осы жағдай үшін
бастапқыда бөлшектер кеңістікте хаосты
бағытта, яғни орташалағанда изотропты
болады деп аламыз. Инерция центрі санақ
жүйесінде (и.ц.с.ж.) барлық ыдыраған
бөлшектер (тегі бірдей) бірдей энергияға
ие, ал олардың ұшу бағыттары изотропты.
Бұл жоғарыда айтылғандай, бөлшектердің
бастапқы бағыттарының хаостығынан
шығады.
екеуі де болады. Негізінде физикада
осындай ыдырауларды тек бір ғана бөлшек
үшін емес, көптеген бірдей бөлшектер
үшін қарастыру керек. Сондықтан ыдыраған
бөлшектердің бағыттарын, энергияларын
қарастыру қажет болады. Осы жағдай үшін
бастапқыда бөлшектер кеңістікте хаосты
бағытта, яғни орташалағанда изотропты
болады деп аламыз. Инерция центрі санақ
жүйесінде (и.ц.с.ж.) барлық ыдыраған
бөлшектер (тегі бірдей) бірдей энергияға
ие, ал олардың ұшу бағыттары изотропты.
Бұл жоғарыда айтылғандай, бөлшектердің
бастапқы бағыттарының хаостығынан
шығады.
![]() денелік бұрышта ұшып келе жатқан
бөлшектердің үлесі осы бұрыштың
элементіне тәуелді:
денелік бұрышта ұшып келе жатқан
бөлшектердің үлесі осы бұрыштың
элементіне тәуелді:
![]() ;
;
![]() (3);
(3);
![]() (4)
Л.с.ж. бөлшектердің таралуын жазу үшін
осы санақ жүйесіндегі кинетикалық
энергияның таралуын қарастырайық.
(4)
Л.с.ж. бөлшектердің таралуын жазу үшін
осы санақ жүйесіндегі кинетикалық
энергияның таралуын қарастырайық.
![]() квадраттап
квадраттап
![]() ;
;![]()
![]() (5);
(5);
![]() ;
;
![]() (6);
Кинетикалық энергияның екі мәні болуы
мүмкін:
(6);
Кинетикалық энергияның екі мәні болуы
мүмкін:
 (7)
(7)
Бөлшектер
бұл интервалда біртекті таралады. Ал
бөлшектің екіге ыдырауымен салыстырғанда,
екіден көп бөлшектерге ыдырағанда,
импульстің және энергияның сақталу
заңдарын қолдану бұндай эффективті
болмайды. Мысалы, и.ц.с.ж. ұшып, бөлініп
шыққан бөлшектердің энергиясының
мәндерінің қатынасы белгісіз болады.
Бірақ әрбір ыдыраған бөлшектің өзімен
бірге ажыратып алып кететін кинетикалық
энергияның белгілі бір жоғарғы шегі
бар. Осы шекті есептейік. Ол үшін белгілі
бір
![]() бөлшектен басқа барлық ыдыраған
бөлшектерді бір жүйе ретінде қарастырып,
оның ішкі энергиясын
бөлшектен басқа барлық ыдыраған
бөлшектерді бір жүйе ретінде қарастырып,
оның ішкі энергиясын
![]() деп белгілейік. Сонда массасы
ыдыраған бөлшектің кинетикалық энергиясы:
деп белгілейік. Сонда массасы
ыдыраған бөлшектің кинетикалық энергиясы:
![]() (8);
– бастапқы бөлшектің массасы.
(8);
– бастапқы бөлшектің массасы.
![]() – ыдырау энергиясы болса:
– ыдырау энергиясы болса:
![]() ;
Егерде
;
Егерде
![]() болса,
болса,
![]() – барынша жоғары мәнді иеленеді. Ол
үшін
бөлшектен басқа бүкіл ыдыраған бөлшектер
бірдей жылдамдықпен қозғалу керек.
Сонымен:
– барынша жоғары мәнді иеленеді. Ол
үшін
бөлшектен басқа бүкіл ыдыраған бөлшектер
бірдей жылдамдықпен қозғалу керек.
Сонымен:
![]() (9)
(9)
