49. Теорема Лейбница

Рассмотрим поcледов. положит. чисел a₁ , a₂ , a₃ … a_n >0 составим ряд a₁ -a₂ +a₃ - a₄ +… +(-1)^n-1a_n + …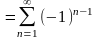 (1)- знакочередующийся.

Признак Лейбница. Если для знакочередующегося ряда (1) выполняется:

1. a1 >a2 >a3 >…

2. - ряд сходится

Ряды, для которых выполняются условия теоремы Лейбница, называются рядами Лейбница

Следствие: Если у ряда (1) a₁ - a_{2 +} a₃ – a₄ +… + (-1)^n-1 a_n + (-1)ⁿ a_n+1 +…

Если отбросить n первых членов, то остаток ряда M_n = (-1)ⁿ a_n+1 +…

________________________________________________________________

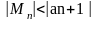
50.Степенные ряды. Теорема Абеля.

Рассмотрим ряд, составленный из степенных функций. Ряд вида: с₀+ с₁х+с₂х²+ с₃х³+…+lnxⁿ = lnxⁿ (1), где с₀, с₁, с₂ – числа, коэф. ряда. U_n = lnxⁿ, т.е. ряд (1) есть ряд по степеням х.

Степенной ряд – функциональный, составленный из функций.

Если зафиксировать х, придав ему числовое значение, получаем ряд lnx₀ⁿ (2). Если этот ряд сходится, то т. х=х₀ наз.точкой сходимости степенного ряда. Множество всех точек сходимости ряда называется областью сходимости степенного ряда.

Суммой степенной ф. будет некоторая ф. I(x), определенная на области сходимости этого ст. ряда. Обозначаем за Р.

Теорема Абеля.

Если степенной ряд lnx₀ⁿ сходится в некоторой т. х₀≠0, то он сходится и притом абсолютно для всех х, уд. неравенству |x|<|x₀|. Если ряд расходится в нек. т. х₁, то он расходится для всех х, |x|>|x₀|.

Д-во. 1) Т.к. степенной ряд сходится в т. х₀≠0, то lnx₀ⁿ сходится. А если ряд сходится, то по необходимому признаку сходимости lnx₀ⁿ=0. Если последовательность имеет предел, то она ограничена, т.е. сущ. М>0, то | lnx₀ⁿ |<=M.

Рассмотрим общий член ряда в общем виде:

| lnx₀ⁿ |=| lnx₀ⁿ xⁿ/х₀ⁿ|-| lnx₀ⁿ |* | xⁿ/х₀ⁿ |=| lnx₀ⁿ |*| x/х₀|ⁿ<=M*| x/х₀|ⁿ

Обозначим | x/х₀|=q. Тогда M*qⁿ – геом. прогрессия

| x/х₀ |<1 – бесконечно убывающая, ряд сходится. |x|<|x₀|

Тогда по признаку сходимости рядов с полож. Членами по первому признаку сравнения сходимости ряда lnx₀ⁿ – сходится абсолютно.

2) Пусть lnx₀ⁿ – расходится в х₁. |x₂|>|x₁|

Пусть в т. х₂ ряд сходится. Тогда |x₂|<|x₁| по первой части теор. Абеля он должен сходится в т. х₁, но в этой т. известно, что ряд расходится => в т. x₂ сходится не будет.