14. Первообразная и неопределённый интеграл.

Пусть функции f(x) и F(x) определены на интервале (a;b). Если функция F(x) имеет производную на интервале (a;b) и для всех x € (a;b) выполняется равенство F’(x) = f(x), то функция F(x) называется первообразной функции f(x) на интервале (a;b).

Совокупность всех первообразных функции f(x) на интервале (a;b) наз. неопределенным интегралом от функции f(x) на этом интервале и обозначается

Теорема. 2 первообразные одной и той же ф-ции отличаются на постоянные слагаемые.

15. Свойства неопределённого интеграла.

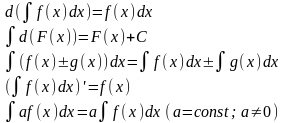
20. Интегрирование рациональных дробей.

Рацион.ф-цией назыв. ф-ция R(x), кот. явл. отношением двух многочленов.

Теорема. Любой многочлен с действ.коэффициентами степени≥2 представим в виде произведения сомножителей линейных и квадратичных вида .

Интегрирование неправ.рац.дробей сводится к интегрированию прав.рац.дробей.

Метод сведения интеграла к интегралу от рац.дроби назыв. методом рационализации.

22. Интегрирование правильных рациональных дробей.

Прав.рац.дробь вида 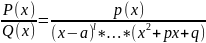можно представить в виде суммы простейших рац.дробей.

26. Определённый интеграл.

Если сущ. предел интегральной суммы , не зависящий от разбиения и выбора точек на каждом отрезке, то этот предел назыв. определенным интегралом f(x) на [a,b] и обозначается

Если сущ. опред.интеграл, то ф-ция назыв. интегрируемой на [a,b].

Замечание 1. При постоянных пределах интегрирования опред.интеграл представляет собой число, а неопред.интеграл – мн-во ф-ций.

Замечание 2. Интегральная сумма не зависит от того, какой буквой обозначена переменная интегрирования.

Замечание 3. Геометрический смысл опред.интеграла. Если f(x)≥0 и непрерывна на [a,b], то (площадь крив.трапеции, ограниченной графиком y=f(x) на отрезке [a,b].

29. Интеграл с переменным верхним пределом.

Функция вида , где x называется интегралом c переменным верхним пределом

_{Теорема: Если} непрерывна на 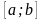, то производная функции , существует в каждой точке на , причем

Теорема 1: если y=f(x) непрерывна на [a,b], то F(x)= f(t)dt непрерывная функция на [a,b]

Теорема 2 (теорема Барроу): если f(x) непрерывна на [a,b] то производная от определ. интеграла с переменным верхним пределом

(f (t)dt) ′ =f (x)

Ф′(x) = ( (f (t)dt))’=f (x)

Из теоремы Барроу следует, что определенный интеграл с переменным верхним пределом является первообразной для подинтегрируемой функции.

Ф′(x) = ( ( f (t)dt))’=f (x)

Этим устанавливается связь между определенным и неопределенным интегралами в случае, когда f(x) непрерывна на [a,b].

30. Формула Ньютона-Лейбница.

Теорема. Если непрерывна на , справедлива формула Ньютона-Лейбница:

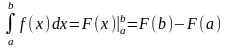
ВЫВОД ФОРМУЛЫ: Рассмотрим , т.к. , то - первообразная для . Но , также первообразная. Это значит что имеет место следующее равенство :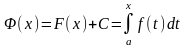

Подставим верхнюю границу:

подставами вместо :

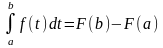в силу 1-го свойства, что значении определенного интеграла независит от обозначения переменной интегрирования, запишем: