Вычисление площадей в декартовых координатах

Если плоская фигура ограничена прямыми х=а, у=в (а<в) и кривыми у=у1(х), у=у2(х), причем у1(х) у2(х), (а х в), то ее площадь вычисляется по формуле

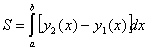
Вопрос 17

Вопрос 18

ФОРМУЛА ОБЪЕМА ТЕЛА ВРАЩЕНИЯ.

Если криволинейная трапеция, ограниченная осью ОХ, прямыми и и кривой графика функции , вращается вокруг оси ОХ, то в пространстве образуется тело , называемое телом вращения. Сечения тела плоскостями , перпендикулярными оси ОХ, являются круги радиуса , поэтому . Тогда .

Вопрос 19

П.2 ДЛИНА ДУГИ КРИВОЙ.

ФОРМУЛА ВЫЧИСЛЕНИЯ ДЛИНЫ ДУГИ, заданной параметрически.

Если дуга кривой задана параметрическими уравнениями , , в которых функции имеют непрерывные производные, то

.

Для ее доказательства заметим, что разбиение порождает разбиение дуги кривой точками и длину ломанной , где и .По теореме о среднем для производной существует набор и точек на отрезках , для которых и . Тогда длина ломаной равна

.

Полученное выражение по форме

ФОРМУЛА ВЫЧИСЛЕНИЯ ДЛИНЫ ДУГИ, заданной в полярной системе.

Если , - уравнение кривой в полярной системе координат, то

. Тогда и .

Вычислим и получим искомую формулу

.

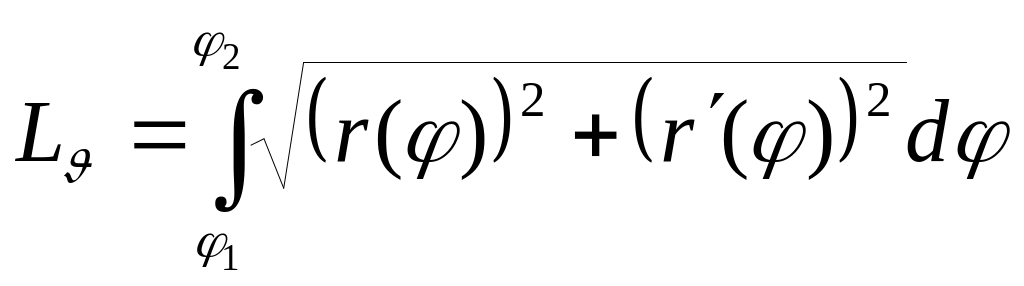№22 Понятие дифференцируемости функции нескольких переменных ,необходимое условие дифференцируемости.

. Функция называется дифференцируемой в точке , если ее приращение можно представить в виде

, где А и В – константы, - бесконечно

малая более высокого порядка , чем .

Функции можно придать вид ,

где бесконечно малые функции в точке (0,0).

Действительно, , где

- бесконечно малая функция,

- ограниченные функции : , .

Тогда и - бесконечно малые функции (0,0).

Определение дифференцируемости перефразируем так : Функция называется дифференцируемой в точке ,если ее приращение можно представить в виде , где А и В – константы, , - бесконечно малые функции (0,0).

ТЕОРЕМА 1. ( Необходимое условие дифференцируемости)

Если функция дифференцируема в точке , то она имеет частные производные в этой точке и А= , В= .

ДОК. При отношение имеет предел при равный А. При отношение имеет предел при равный В.

Вопрос 23

Вопрос 28

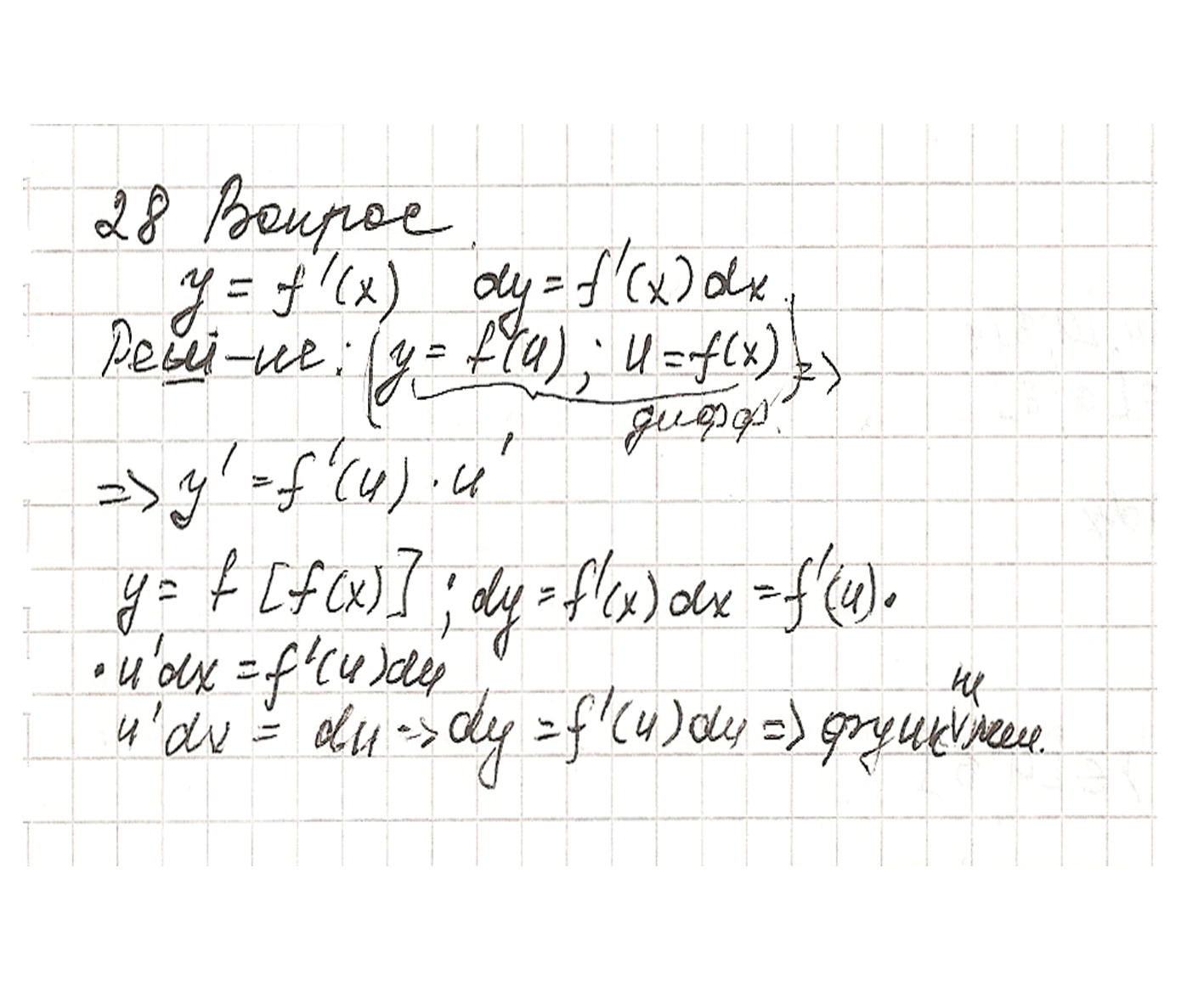
№29 Понятие градиента функции ,производная функции по направлению и её вычисление с помощью градиента.

ОПР. Вектор , компоненты которого равны частным производным функции , называется градиентом функции в точке .

Тогда производная по направлению равна скалярному произведению вектора градиента на единичный вектор направления . Из такого представления производной следует, что градиент указывает направление , в котором функция быстрее всего растет и указывает наибольшее значение производной.

Если уравнение задает поверхность в пространстве и дифференцируемая кривая на этой поверхности : для , то

, где - касательный вектор к кривой . Таким образом, вектор градиента функции в точке перпендикулярен касательному вектору к любой кривой, проходящей через эту точку. Следовательно, вектор градиента является нормальным вектором к касательной плоскости к поверхности в точке .

Производная по направлению, градиент функции.

Рассмотрим приращение функции в направлении единичного вектора : .

ОПР. Производной функции в точке в направлении вектора называют число .

ФОРМУЛА ДЛЯ НАХОЖДЕНИЯ ПРОИЗВОДНОЙ по направлению.

Если функция дифференцируема в точке , то .

ДОК. = .

Вопрос 30

Вопрос 31

Вопрос 32

Вопрос 34

Несобственный интеграл от неограниченной функции на конечном отрезке.

Пусть функция непрерывна на и неограниченна на каждом из интервалов

.

ОПР. Несобственным интегралом функции на отрезке называют число

.

Если несобственный интеграл существует, то говорят о сходящемся интеграле. Если предел не существует или он бесконечный, то говорят о расходимости интеграла.

ПРИМЕР 1. При каких существует интеграл ?

РЕШЕНИЕ. = , если .

Если , то . Если , то .

Таким образом, в примере 1 интеграл сходится при и расходится при .