4. Основні поняття теми, їх логіко-дидактичний аналіз.

Визначення поняття виконує три важливі пізнавальні функції.

• у визначенні розкривається зміст і обсяг поняття;

• указується на відмінність, предмета, який визначається, від усіх інших предметів;

• уточнюється значення терміна, яким позначається предмет.

Визначити поняття – значить перерахувати його істотні ознаки, які виражають природу предмета та його відмінність від інших предметів.

Поняття «Паралелограм» - родовидове. При складанні "родовидового" визначення поняття, отримаємо, що:

Паралелограм - це чотирикутник, у якого протилежні сторони паралельні.

Чотирикутник - фігура, яка складається з чотирьох точок і чотирьох послідовно з'єднуючих їх відрізків.

Інакше кажучи, родовід представляє собою ланцюжок понять, побудованих через узагальнення попереднього поняття, фіналом якої є невизначені поняття (нагадаємо, що в курсі шкільної геометрії до таких належать точка, фігура, площину, відстань (лежати між)).

Термін	Поняття
Чотирикутник	Опуклий многокутник з 4 сторонами
Паралелограм	Чотирикутник у якого протилежні сторони попарно паралельні і рівні
Сусідні вершини	Вершини, що являються кінцями однієї сторони
Протилежні вершини	Не сусідні вершини
Сусідні сторони	Сторони, що мають спільну вершину
Протилежні сторони	Не мають спільної вершини
Діагональ	Відрізок, що сполучає протилежні вершини

5. Твердження, що вивчаються, та їх види.

Математика має справу з твердженнями, які доводяться (теореми, задачі на доведення), і такими, що їх домовляються приймати без доведення (аксіоми).

До теорем (задач, що доводяться) відносять:

• Ознаку

• Властивість.

Властивості паралелограма

Теорема_1. у паралелограмі протилежні сторони рівні, протилежні кути рівні.

Теорема_2. Діагоналі паралелограма перетинаються і точкою перетину діляться пополам.

Теорема_3. У паралелограмі кути, прилеглі до однієї сторони, в сумі дорівнюють 180⁰

Ознаки паралелограма

Теорема_4. Чотирикутник, у якого діагоналі перетинаються і точкою перетину діляться пополам, то такий чотирикутник – паралелограм.

Теорема_5. Якщо в чотирикутнику протилежні сторони попарно рівні, то такий чотирикутник є паралелограмом.

Теорема_6. Якщо в чотирикутнику пара протилежних сторін рівна і паралельна, то даний чотирикутник є паралелограмом.

Теорема_7. Якщо в чотирикутнику протилежні кути рівні, то він паралелограм.

При вивченні теми «Паралелограм та його властивості. Ознаки паралелограма» теореми є:

• прямі;

• обернені.

З курсу геометрії 7 класу відомо, що більшість теорем складаються з двох частин: умови (те, що дано) і висновку (те, що треба довести).

Якщо твердження, яке виражає умову, позначити буквою Α, а твердження, яке виражає висновок, - буквою В, то формулювання теореми можна зобразити такою схемою:

Якщо А, то В.

Наприклад теорему_2 можна сформулювати так:

Якщо , то .

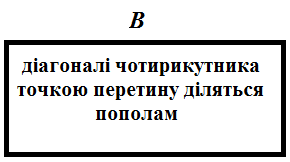Тоді теорему_4 можна сформулювати так:

Якщо , то .

Часто в повсякденному житті у висловлювання люди користуються словами «необхідно» і «достатньо». Наведемо кілька прикладів.

• Для того, щоб уміти розв’язувати задачі, необхідно знати теореми.

• Якщо ви на математичній олімпіаді розв’язали правильно всі запропоновані задачі, то цього достатньо для того, щоб здобути перше місце.

• Для того, щоб стрілець влучив у мішень В (рис.1), йому достатньо влучити в мішень А. Для того, щоб влучити в мішень А, необхідно влучити в мішень В.

Н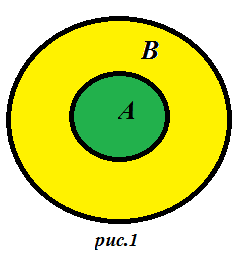 аведемо приклад.

Твердження А	Твердження В	Зв'язок між твердженнями	Вид умови
Чотирикутник є паралелограмом	Дві протилежні сторони чотирикутника рівні	З А випливає В (А→В)	А – достатня умова для В
			В – необхідна умова для А
Чотирикутник є паралелограмом	Діагоналі точкою перетину діляться пополам	З А випливає В і з В випливає А (А↔В)	А – необхідна і достатня умова для В і навпаки

Отже, теорема_1 є прямою теоремою, теорема_2 і теорема_4 є взаємно оберненими (тобто, обернена теорема до прямої). Мовою «необхідно-достатньо» цей факт можна сформулювати одним з двох способів:

• для того, щоб чотирикутник був паралелограмом, необхідно і достатньо, щоб його діагоналі точкою перетину ділилися пополам;

• для того, щоб діагоналі чотирикутника точкою перетину ділилися пополам, необхідно і достатньо, щоб цей чотирикутник буа паралелограмом.

Отже, коли в теоремі є слова «необхідно» і «достатньо», то вона обєднує дві теореми: пряму і обернену.

Іноді замість «необхідно» і «достатньо» говорять «тоді і тільки тоді».

Отже, необхідна умова дає нам властивість, а якщо умова не тільки необхідна, але й достатня, то одержуємо ознаку.