Моделирование синхронного двигателя с массивным ротором в пакете matlabsimulink о.В. Бондаренко, в.А. Шабанов

(Уфимский государственный нефтяной технический университет, г.Уфа)

Для исследования переходных процессов в синхронных двигателях (СД) магистральных насосов (МН) нефтеперекачивающих станций НПС при изменении частоты вращения частотно-регулируемого электропривода (ЧРЭП) МН необходимо иметь математическую модель электродвигателя. Моделирование электромеханических процессов в синхронном двигателе производится на основе системы дифференциальных уравнений обобщенной двухфазной машины переменного тока с демпферной обмоткой [1, 2, 3].

При моделировании СД принимаются следующие допущения [1, 4]:

- не учитываются потери в стали;

- не учитываются высшие гармоники магнитного поля при равномерном воздушном зазоре;

- напряжение питания является симметричной системой синусоидальных напряжений;

- нулевой ток отсутствует, сумма мгновенных значений фазных токов равна нулю;

- каждый протекающий по фазной обмотке ток порождает магнитодвижущую силу, синусоидально распределенную по окружности воздушного зазора машины;

- сложение магнитодвижущих сил отдельных фазных обмоток порождает общую магнитную индукцию, также синусоидально распределенную по окружности воздушного зазора;

- характеристика намагничивания машины линейна;

- параметры роторной цепи приведены к статорному контуру.

Переход от трехфазной машины к двухфазной осуществляется через пространственные вектора токов, напряжений, потокосцеплений. Проекции i_x и i_y пространственного вектора тока статора на оси неподвижной системы координат [1, 5]

; (1)

М атематическая модель электромагнитных процессов в СД с демпферной обмоткой представляется в виде системы уравнений для проекций обобщенных векторов на оси d и q вращающейся системы координат в именованных единицах [1, 2]:

;

;

;

;

;

; (2)

;

;

;

;

.

где u_d, u_q- проекции пространственного вектора напряжения на оси вращающейся системы координат d-q

;

;

R, R_f – активные сопротивления фазы обмотки статора и обмотки возбуждения соответственно; i_d, i_q– токи статора по продольной d и поперечной q осям; ψ_d, ψ_q - потокосцепления обмоток статора по осям d и q;i_f- ток возбуждения; ψ_f – потокосцепление обмотки возбуждения; R_kd, R_kq - активные сопротивления демпферной обмотки по осям d и q;i_kd, i_kq– токи демпферной обмотки по осям d и q; ψ_kd, ψ_kq - потокосцепления демпферной обмотки по осям d и q; L_d, L_q и L_f - полные индуктивности обмоток статора по осям d и q и полная индуктивность обмотки возбуждения соответственно; L_ad, L_aq- взаимная индукция между обмоткой возбуждения и обмотками статора по осям d и q; L_σ, L_fσ - индуктивности рассеяния обмотки статора и обмотки возбуждения соответственно;L_kd, L_kq– полные индуктивности демпферной обмотки (массивного ротора) по осям d и q; L_kdσ, L_kqσ -индуктивности рассеяния демпферного контура по осям d и q; р_п – число пар полюсов; ω – угловая скорость вращения ротора.

Угол нагрузки СД

(3)

где ω₀ – угловая скорость вращения вращающегося магнитного поля.

Параметры роторных контуров (токи, сопротивления, напряжения) должны быть приведены к обмотке статора через коэффициенты приведения [6]

; ; ; ; , (4)

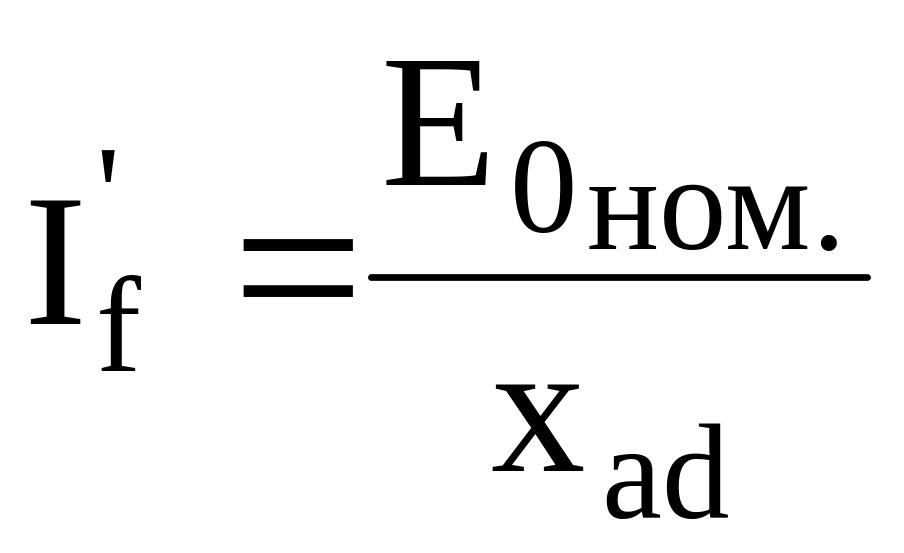где , (5)

В СД серии СТД массивный ротор выполняет функции демпферного контура, активное и индуктивное сопротивления которого изменяются при изменении частоты вращения [7, 8]:

; (6)

, (7)

где , - активное (индуктивное сопротивления рассеяния) эквивалентного демпферного контура при пуске (s=1) и в синхронном режиме (s=0).

В литературе [8] значения активных и индуктивных сопротивлений СД задаются в относительных единицах. Перевод значений сопротивлений из относительных единиц в именованные производится на основе формулы

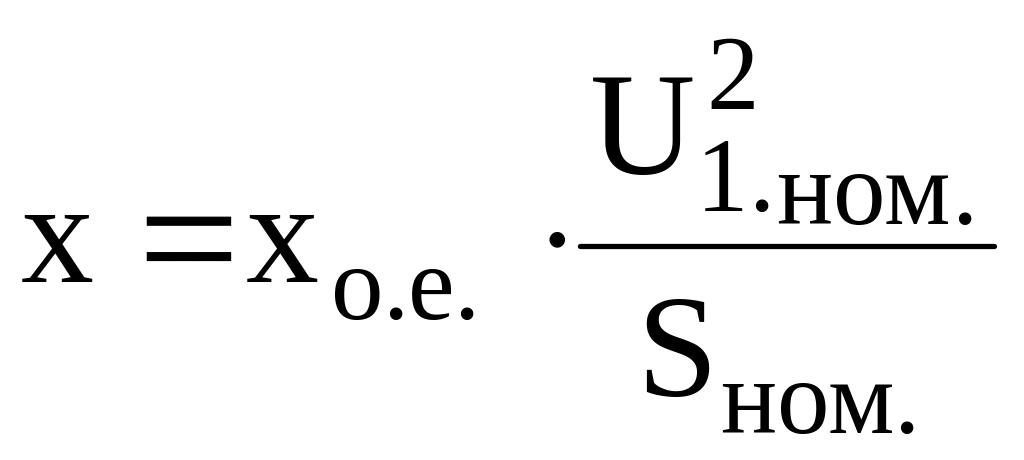(8)

где х_о.е. – значение сопротивления в относительных единицах; - номинальное линейное напряжение.

Математическая модель СД с массивным ротором на основе системы дифференциальных уравнений (2) представлена на рисунке 1. На вход модели (рисунок 1) подаются мгновенные значения напряжений фаз А, В, С, коэффициент тока возбуждения k_f, значение момента сопротивления насоса M_c. На выходе модели снимаются значения частоты вращения и угла нагрузки. Параметры модели рассчитываются в блоке Parametr. Для задания начального синхронного режима необходимо в схеме установить на выходах соответствующих интеграторов начальные значения проекций пространственных векторов потокосцепления статора , , ротора , демпферного контура , , значения частоты вращения и угла нагрузки .

Начальные значения проекций пространственных векторов потокосцепления статора, ротора, демпферного контура, определяются в матричной форме по выражению [1]

А∙х=u(9)

; (10)

Графики изменения электромагнитного момента частоты вращения и угла нагрузки СД, типа СТД-8000 при изменении момента сопротивления (от 0 до 20000 Н∙м) на 1-й секунде и изменения частоты питающего напряжения (с 50 до 49 Гц) на 7-й секунде показаны на рисунке 2. Технические параметры СД, используемые в расчетах, приведены в приложении.

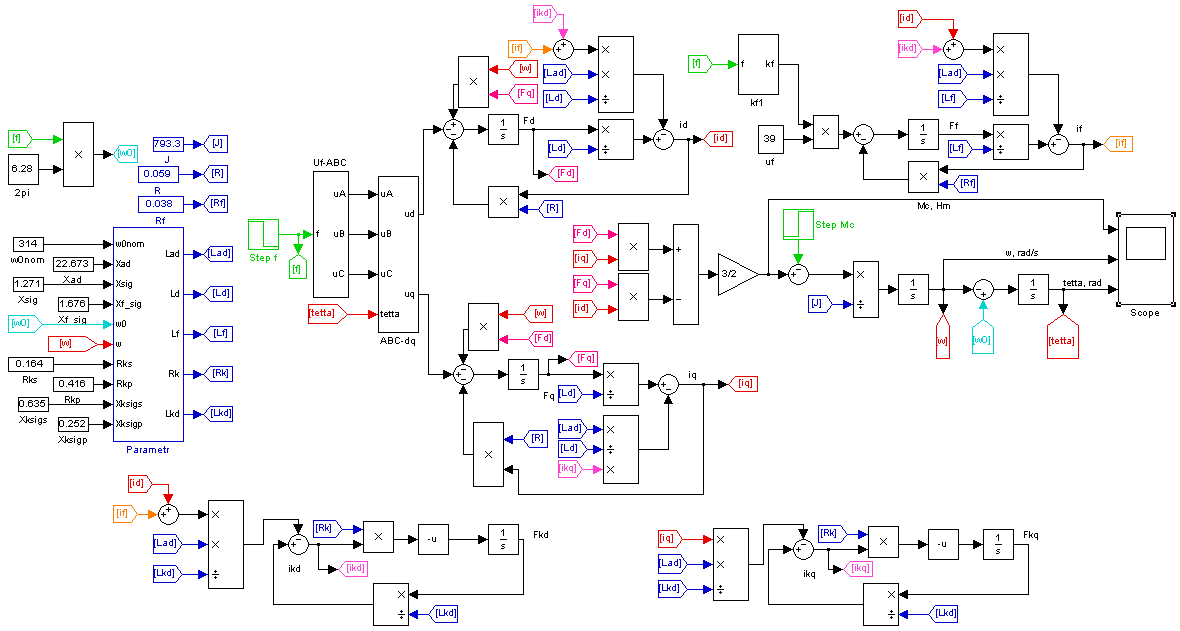
Р исунок 1 – Структурная схема модели синхронного двигателя в MatlabSimulink

Рисунок 2 – Графики переходных процессов момента СД

Таким образом, с помощью созданной в пакете MatlabSimulink модели СД серии СТД могут быть исследованы переходные процессы при изменении частоты напряжения питания, а также момента сопротивления магистрального насоса.

Приложение –Технические данные двигателя СТД-8000 [8, 9, 10]

Технические данные	Значения
Номинальная мощность Рном., кВт	8000
Номинальное напряжение U1ном., В	10000
Номинальный ток статора I1ном., A	527
Сопротивление обмотки статора при 15ºС R1, Ом	0,0476
Активное сопротивление эквивалентного демпферного контура в синхронном режиме , о.е.	0,015
Активное сопротивление эквивалентного демпферного контура при пуске , о.е.	0,038
Синхронное реактивное сопротивление статора xd,%	219,2
Сопротивление взаимоиндукции между статорной и роторной обмотками , о.е.	2,07
Индуктивное сопротивление рассеяния статорной обмотки , о.е.	0,116
Индуктивное сопротивление рассеяния обмотки возбуждения , о.е.	0,153
Индуктивное сопротивление рассеяния эквивалентного в синхронном режиме демпферного контура , о.е.	0,058
Индуктивное сопротивление рассеяния эквивалентного демпферного контура при пуске , о.е.	0,023
Номинальный ток возбуждения, If.ном., А	261, 6
Номинальное напряжение возбуждения, Ufном.	156,0
Сопротивление обмотки возбуждения при 15ºС Rf., Ом	0,417
Приведенное сопротивление обмотки возбуждения , Ом	0,038
Момент инерции двигателя J, кг∙м2	767
Момент инерции насоса НМ 10000-210, Jн., кг∙м2	26,3

СПИСОК ЛИТЕРАТУРЫ

1 Соколовский Г.Г. Электроприводы переменного тока с частотным регулированием. – М.: Изд. центр Академия, 2006. – 272 с.

2Калентионок Е.В. Устойчивость электроэнергетических систем. Минск: Техноперспектива, 2008. - с. 376

3 Абрамович Б.Н., Жуковский Ю.Л., Круглый А.А., Устинов Д.А. Моделирование электромеханических комплексов с синхронными двигателями в системе проведения математических расчетов Matlab пакет Simulink. – Спб.: Изд-во Нестор, 2007. – с. 59.

4 Тумаева Е.В. Математическая модель синхронного электропривода: монография. – Казань: Изд-во Казан. Гос. Технол. Ун-та, 2008. - 96 с.

5 Фираго Б.И., Павлячик Л.Б. Регулируемые электроприводы переменного тока. – Минск: Техноперспектива, 2006. - 363 с.

6 Вольдек А.И., Попов В.В. Машины переменного тока: учеб. для вузов. – СПб.: Питер, 2008. – 350 с

7 Сыромятников И.А. Режимы работы асинхронных и синхронных двигателей – М.: Энергоатомиздат 1984. 240 с.

8 Гамазин С.И., Ставцев В.А., Цырук С.А. Переходные процессы в системах элетроснабжения, обусловленные электродвигательной нагрузкой. – М.: Изд-во МЭИ, 1997. – 424 с.

9 РД 39-0147103-307-85. Методика определения КПД насосных агрегатов магистральных нефтепроводов. 1986. 35 с.

10 Першина Л.М., Бак С.И., Першин Ю.С., Читипаховян С.П. Применение электродвигателей в нефтяной промышленности - М.: Недра, 1980. – 167 с.

УДК 621.313