Оптимизация режима работы синхронного двигателя магистрального насоса нпс при частотном регулировании о.В. Бондаренко, в.А. Шабанов

(Уфимский государственный нефтяной технический университет, г.Уфа)

Для обеспечения оптимального режима работы частотно-регулируемых электроприводов (ЧРЭП) магистральных насосов (МН) НПС необходимо выбрать оптимальный закон скалярного частотного управления синхронным двигателем (СД). В скалярной системе управления электроприводом токи и напряжения рассматриваются как скалярные величины. Для СД параметрами закона частотного регулирования являются частота напряжения питания, действующее значение напряжения на статоре и значение тока возбуждения. Известны скалярные законы частотного регулирования СД [1, 2]. Однако эти законы не учитывают изменение КПД и коэффициент мощности СД, а также потери мощности от токов высших гармоник и поэтому их нельзя рассматривать как оптимальные.

Оптимальный закон частотного регулирования можно определить в результате решения оптимизационной задачи по критерию минимума потерь мощности СД:

, (1)

где суммарные потери мощности должны определяться с учетом влияния, как регулируемых параметров, так и токов высших гармоник.

Суммарные потери мощности СД можно записать в виде:

, (2)

где - потери в обмотке статора; - магнитные потери; - потери на возбуждение; - механические потери; - добавочные потери [3, 4]; - потери, обусловленные наличием высших гармоник напряжения и тока.

Потери в обмотке статора пропорциональны квадрату тока статора I₁:

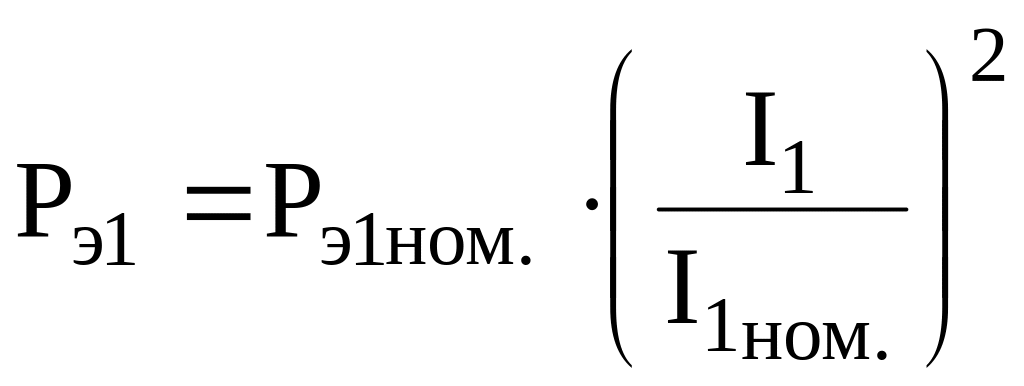, (3)

где - потери в обмотке статора в номинальном режиме,

; (4)

I_1ном. – номинальный ток статора; R₁ - активное сопротивление обмотки статора.

Представим ток статора через составляющие по осям d и q [5]

, (5)

где составляющие тока статора при частотном регулировании

; , (6)

где ;U₁- напряжение статора;U_1ном. – номинальное напряжение; U_1ф.ном. – номинальное фазное напряжение; и x_q- синхронные индуктивные сопротивления обмотки статора по продольной и поперечной осям; - ЭДС возбуждения при номинальном режиме; ; f – частота напряжения питания статора; f_ном. – номинальная частота; θ – угол нагрузки

, (7)

где M_c - момент сопротивления на валу СД;

М_maxf - максимальное значение синхронного момента при частоте напряжения питания статора f,

;

- максимальное значение синхронного момента при номинальной частоте:

;

. (8)

Магнитные потери[4, 5, 6]

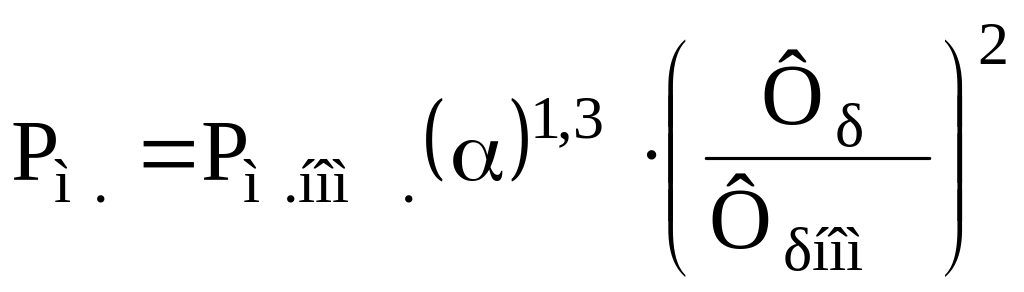, (9)

где - потери в магнитопроводе статора в номинальном режиме;

- результирующий магнитный поток в воздушном зазоре;

- магнитный поток в воздушном зазоре для номинального режима.

Учитывая, что ЭДС пропорциональна величине результирующего магнитного потока и его частоте, отношение магнитных потоков можно представить в виде [5]

, (10)

где и - значения ЭДС от результирующего магнитного потока при частотном регулировании и номинальном режиме.

Выражение для магнитных потерь (9) с учетом (10) принимает вид

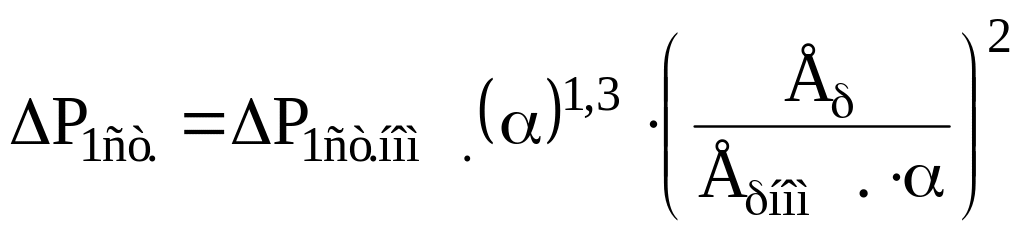, (11)

Значение ЭДС от результирующего магнитного потока при частотном регулировании может быть найдено по выражению [5]

,

где х_σ - индуктивное сопротивление рассеяния обмотки статора.

Потери на возбуждение[4]

, (12)

где R_f – активное сопротивление обмотки возбуждения; ; I_f–ток возбуждения; I_f.нoм. –номинальный ток возбуждения; ΔU_щ – переходное падение напряжения в щеточном контакте ΔU_щ= 1 В.

Механические потерипропорциональны третьей степени частоты[4]

, (13)

где - механические потери в номинальном режиме.

Из добавочных потерь выделим потери от наведенных потоками рассеяния вихревых токов [7]

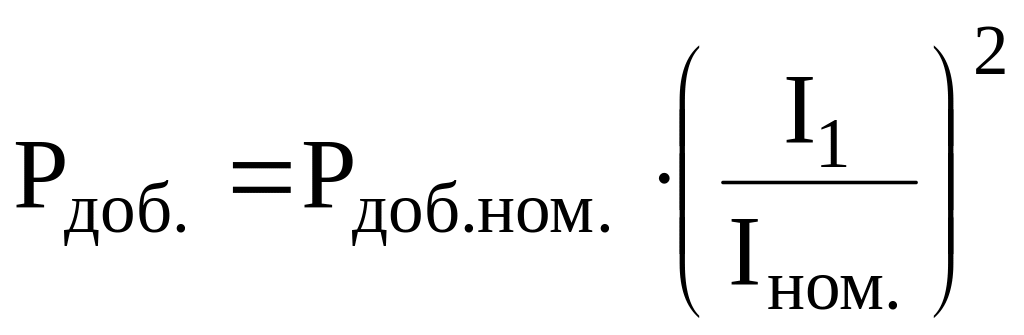, (14)

где - добавочные потери от наведенных потоками рассеяния вихревых токов в номинальном режиме.

Потери, обусловленные наличием высших гармоник напряжения, определяются через напряжения гармоник на выходе ПЧ

, (15)

где k_г – коэффициент, для СД без демпферной обмотки k_г=0,4; U_ν– напряжение ν-той гармоники на выходе ПЧ, %; ν – номер гармоники; P_ном. – номинальная мощность двигателя [8];

Из формул (3), (9), (12), (13), (14) и (15) вытекают следующие свойства потерь мощности в СД. Потери в обмотке статора по (3) и добавочные потери по (13) пропорциональны квадрату тока статора, который в соответствии с (6) увеличивается при снижении частоты и снижается при снижении напряжения на статоре. Поэтому при одновременном снижении частоты и напряжения на статоре потери в обмотке статора и добавочные потери при нагрузке могут, как увеличиваться, так и уменьшаться. Магнитные потери по (11) снижаются по мере снижения частоты напряжения питания статора и напряжения на статоре. Потери на возбуждение по (12) определяются током возбуждения. Механические потери по (13) снижаются при снижении частоты питания статора и не зависят от напряжения на статоре. Потери от высших гармоник по (15) зависят от гармонического состава напряжения на выходе ПЧ, то есть от типа ПЧ.

Таким образом, при частотном управлении влияние регулируемых параметров , и на отдельные составляющие потерь мощности, а, следовательно, и на суммарные потери мощности и КПД регулируемых СД не однозначно. При этом для каждого типа двигателя может существовать оптимальное соотношение регулируемых параметров, при котором потери мощности в процессе регулирования будут минимальными.

Для привода МН широко используются СД. Основными преимуществами СД являются их способность генерировать в сеть реактивную мощность и работать с коэффициентом мощности, равным единице. При работе в составе ЧРЭП из названных преимуществ наиболее важным является способность работать с единичным коэффициентом мощности. При этом СД потребляет от ПЧ только активную мощность, что снижает ток в силовых ключах ПЧ и повышает его КПД. Обозначим угол между током статора и осью d через ψ. Тогда для суммы углов φ и θ можно записать ψ= φ + θ [5]. Из этого выражения при единичном коэффициенте мощности получаем:

. (16)

Одним из недостатков скалярного управления СД принято считать возможность потери статической устойчивости. Запас по устойчивости характеризуют коэффициентом запаса. Для обеспечения устойчивости СД при ЧР коэффициент запаса в процессе регулирования не должен снижаться ниже некоторого (требуемого или заданного) значения k_зад. При этом для запаса устойчивости по моменту можно записать

. (17)

Если при минимизации целевой функции (2) учесть ограничения (16) и (17), то при частотном регулировании будет поддерживаться единичный коэффициент мощности и заданный запас статической устойчивости.

В соответствие с приведенными выше выражениями (1)–(17) для определения оптимального закона частотного регулирования СД была разработана программа в пакете Matlab. Программа содержит две встроенные M-функции: KPDOpt(x). и GL(x). В первой из них задаются технические данные СД, и формулы для расчета потерь. В функции GL(x) задаются нелинейные ограничения (16) – (17).

Исходными данными для расчета оптимального режима работы СД при частотном регулировании являются:

- паспортные параметры двигателя: номинальная мощность СД, номинальное напряжение, номинальный ток статора, номинальная мощность СД, номинальная частота, номинальный коэффициент мощности, активное сопротивление обмотки статора, индуктивное сопротивление статора, индуктивное сопротивление рассеяния обмотки статора, номинальный ток возбуждения, сопротивление обмотки возбуждения, номинальные потери в стали, номинальные механические потери, номинальные добавочные потери, гармонический состав напряжения на выходе ПЧ;

- паспортные данные ПЧ: гармонический состав напряжения на его выходе;

- регулируемыми параметрами при ЧР СД являются частота, напряжение и ток возбуждения. В данной программе находятся оптимальные значения напряжении и тока возбуждения для заданных значений частоты.

В рабочей области CommandWindow задаются: вектор начальных приближений, дополнительные ограничения (0<γ≤1, 0<k_f≤1) на напряжение статора и ток возбуждения и функция fmincom, с помощью которой по методу последовательного квадратичного программирования ‘sqp’ минимизируется целевая функция (рисунок 1).

Рисунок 1 – Листинг программы расчета оптимального режима работы СД

В таблице 1 для значений α от 0,1 до 1,0 представлены результаты расчета значений напряжения статора и тока возбуждения в относительных единицах при частотном регулировании СД серии СТД-8000, технические данные которого представлены в таблице 2. При расчетах принято, что коэффициент запаса устойчивости по моменту равен 0,2, При этом угол нагрузки поддерживается не ниже . Принято, что момент сопротивления магистрального насоса изменяется пропорционально α, что объясняется влиянием режима перекачки нефти. Гармонический состав напряжения на выходе ПЧ приведен в таблице 3.

Таблица 1 – Значения напряжения на статоре и тока возбуждения в относительных единицах при оптимальном законе частного регулирования, потери мощности, КПД

α, о.е.	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
γ, о.е.	0,07	0,14	0,23	0,34	0,45	0,57	0,69	0,82	0,95	1,0
kf, о.е.	0,20	0,29	0,35	0,40	0,45	0,49	0,53	0,57	0,61	0,695
∑Р, Вт	4048	4514	5181	6064	7199	8617	10354	12444	14922	18124
КПД, %	0,94	0,964	0,976	0,981	0,983	0,984	0,984	0,983	0,983	0,98

Из таблицы 1 видно, что при α=0,4-0,9 КПД СД выше номинального значения. При α=0,1-0,3 КПД СД снижается. Зависимости γ =f(α) и k_f=f(α) представлены на рисунке 2.

Таблица 2 – Технические данные СД серии СТД -8000 [9,11,12]

Технические данные	Значения
Номинальная полная мощность Sном., кВА	9130
Номинальная мощность Рном., кВт	8000
Номинальное напряжение U1ном., В	10000
Номинальный ток статора I1ном., A	527
Номинальный коэффициент мощности cosφном., о.е.	0,9
Сопротивление обмотки статора при 15ºС R1, Ом	0,0476
Синхронное реактивное сопротивление статора xd,%	219,2
Индуктивное сопротивление рассеяния статорной обмотки , о.е.	0,116
Номинальный ток возбуждения, If.ном., А	261, 6
Номинальное напряжение возбуждения, Ufном.	156,0
Сопротивление обмотки возбуждения при 15ºС Rf., Ом	0,417
Приведенное сопротивление обмотки возбуждения , Ом	0,038
Номинальный КПД ηном. %	97,7
Номинальные потери в стали (магнитопроводе статора) , кВт	32
Номинальные механические потери , кВт	64
Номинальные добавочные потери , кВт	18,5

Таблица 3 – Гармонический состав напряжения ПЧ [13]

Номер гармоники	5	7	11	13	17	19
Значение, %	8,8	1,5	0,6	0,3	0,1	0,1

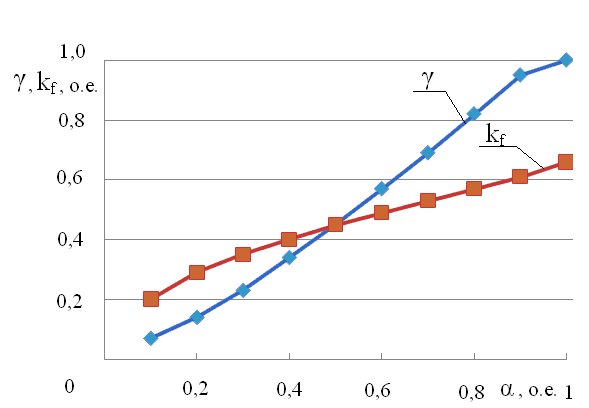
Рисунок 2 - Зависимости γ=f(α) и k_f=f(α) при оптимальном законе регулирования СД

серии СТД

Из рисунка 2 видно, что зависимости γ=f(α) и k_f=f(α) при оптимальном законе регулирования нелинейны.

Выводы

1 Предложена методика выбора регулируемых параметров: напряжения, частоты и тока возбуждения по критерию минимальных потерь мощности в СД при частотном регулировании.

2 В Matlab разработана программа оптимизации режима работы СД по критерию минимума потерь мощности с ограничениями по коэффициенту мощности и углу нагрузки (коэффициента запаса устойчивости).

3 Для СД серии СТД-8000 найдены соотношения между регулируемыми параметрами, при которых потери мощности в СД будут минимальными, а коэффициент запаса устойчивости по мощности не ниже минимального значения 0,2.

СПИСОК ЛИТЕРАТУРЫ

1 Чиликин, М.Г., Сандлер, А.С. Общий курс электропривода. уч. для вузов. - М.: Энергоиздат, 1981. 576 с.

2 Титов М.П. Частотно-регулируемый синхронный электродвигатель. – Братск: БрИИ, 1998. -144 с.

3 Иванов-Смоленский А.В. Электрические машины: учебник для вузов. В двух томах. Том 2. – М.: Издательский дом МЭИ, 2006. - 532 с.

4 Проектирование электрических машин: учебник для вузов/ под ред. И.П. Копылова. – М.: Издательство Юрайт, 2011. – 767 с.

5 Сыромятников И.А. Режимы работы асинхронных и синхронных двигателей – М.: Энергоатомиздат 1984. 240 с.

6 Сергеев А.С., Виноградов Н.В., Горяинов Ф.А. Проектирование электрических машин. - М.: Энергия, 1969. 632 с.

7 Кузнецов С.Е. Потреи и коэффициент полезного действия судового синхронного генератора// Эксплуатация морского транспорта. 2009. № 3(57). С. 67-71.

8 Железко Ю.С. Потери электроэнергии. Реактивная мощность. Качество электроэнергии. – М.: ЭНАС, 2009. – 456 с.

9 Гумеров А.Г., Гумеров Р.С., Акбердин А.М. Эксплуатация оборудования нефтеперекачивающих стаций. . – М.: ООО «Недра –Бизнесцентр», 2001. – 475 с.

10 Методические указания по устойчивости энергосистем(от 30 июня 2003 г.). СО 153-34.20.576-2003. М: НЦ ЭНАС, 2004. –с.16

11 Гамазин С.И., Ставцев В.А., Цырук С.А. Переходные процессы в системах электроснабжения, обусловленные электродвигательной нагрузкой. – М.: Изд-во МЭИ, 1997. – 424 с.

12 РД 39-0147103-307-85. Методика определения КПД насосных агрегатов магистральных нефтепроводов. 1986. - 35 с.

13 Лазарев Г.Б. Мощные высоковольтные преобразователи частоты для регулируемого электропривода в электроэнергетике// Силовая электроника. 2005. №11. С. 3-8.

УДК 621.313