К вопросу о расчете потерь от высших гармоник в синхронных двигателях с массивным ротором д.Е. Ярулин (маэ02-12-01), в.М. Сапельников

(Уфимский государственный нефтяной технический университет, г. Уфа)

В синхронных двигателях с массивным ротором основная доля потерь от токов высших гармоник приходится на обмотку ротора. Мощность, передаваемая токами высших гармоник, не совершает полезной работы и полностью идет на нагрев ротора, что может привести к повреждению обмотки возбуждения.

При протекании токов высших гармоник в электродвигателях возникают дополнительные потери мощности равные[1]

(1)

где – дополнительные потери в меди обмоток; – дополнительные потери в стали; – мощность, идущая на преодоление тормозного момента.

Дополнительные потери в меди статора при номинальной нагрузке определяются по выражению

(2)

где k_п – кратность пускового тока; ΔP_м.н.–потери в меди обмоток при синусоидальном токе при номинальном токе в обмотке статора при отсутствии высших гармоник; U_(n) – действующее значение n-й гармоники;

, (3)

где - эквивалентное сопротивление ротора; - сопротивление ротора;

n- номер гармоники.

В формуле (2) при расчете потерь в меди от токов высших гармоник в качестве базовой величины используются потери в меди ΔP_м.н. в номинальном режиме. Но в роторе СД при отсутствии высших гармоник нет потерь в стали ротора. Так как ротор вращается синхронно с магнитным полем статора, то он не перемагничивается и в теле ротора нет вихревых токов частотой 50 Гц. Раз потерь в теле ротора в синхронном режиме нет, значит их нет и в номинальной мощности потерь ΔР_ст.ном в формуле (2). Следовательно, в выражение (2) при определении коэффициента по формуле (3) не учтены потери в стали ротора от токов высших гармоник. У СД с массивным ротором нет демпферной обмотки. Роль демпферных токов выполняют вихревые токи в теле ротора. Тело ротора с вихревыми токами на схемах замещения представляется эквивалентным контуром. Поэтому, в выражение (2) следует ввести потери от высших гармоник в активном сопротивлении эквивалентного демпферного контура ротора. Сопротивление эквивалентного контура ротора определяется по выражению [2]

, (4)

где - активное сопротивление обмотки возбуждения; - активное сопротивление эквивалентного демпферного контура.

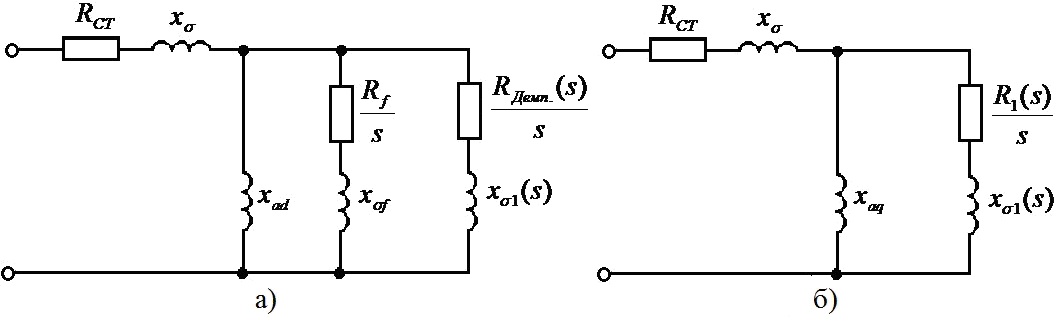
а) по продольной оси ротора d; б) по поперечной оси ротора q

Рисунок 1 – Схемы замещения СД с массивным гладким ротором: по продольной оси ротора

Активное сопротивление статора

, (5)

где - активное сопротивление статора на частоте 50 Гц; - полное сопротивление статора на частоте 50 Гц;

, (6)

где - номинальное напряжение питания СД; - номинальный ток статора.

Потери в меди обмотки статора СД в номинальном режиме

, (7)

где R_1c– сопротивление обмотки статора.

Потери в обмотке возбуждения СД в номинальном режиме

, (8)

где I_в.н. – номинальный ток обмотки возбуждения;R_o.в. – сопротивление обмотки возбуждения.

Общие потери в меди СД в номинальном режиме

. (9)

Знак «плюс» в подкоренном выражении (2) соответствует симмет­ричным составляющим гармоник, вращающимся против вращения поля основнойгармоники, знак «минус» – симметричным составляю­щим гармоник, создающих поле, вращение которых совпадает с вра­щением поля основной гармоники.

Подставляя в формулу (3) выражения для активных сопротивлений статора и приведенного активного сопротивления ротора с учетом демпферного контура, получим

. (10)

При использовании выражения (10) дополнительные потери в меди статора можно определять по выражению (2).

Дополнительные потери в стали определяются по формуле 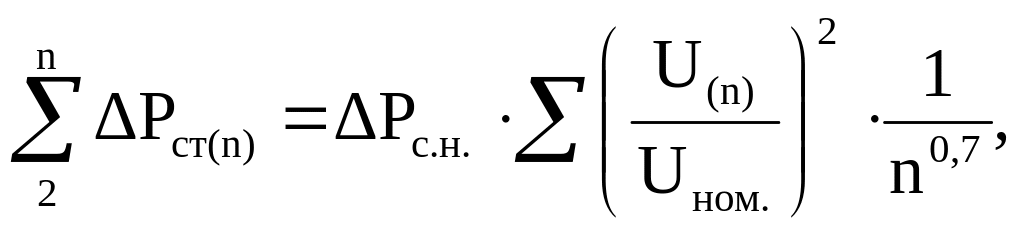[1]:

(11)

где ΔP_с.н. – номинальные потери в стали двигателя при номинальном напряжении U_ном.

Мощность потерь, расходуемая на преодоление тормозного момента от токов высших гармоник

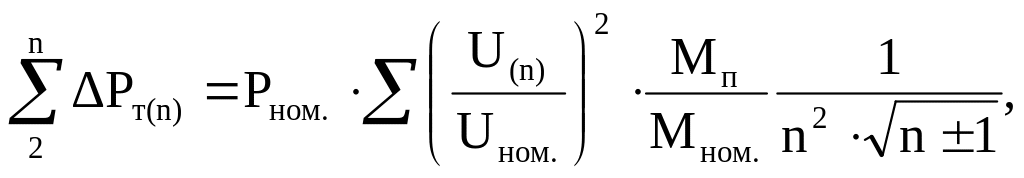(12)

где M_п и M_ном. – пусковой и номинальный моменты синхронного двигателя.

Для вычисления дополнительных потерь по методике изложенной выше все необходимые величины определяются по паспортным или справоч­ным данным для конкретного типа электродвигателя. Значения U(n) могут быть измерены с высокой точностью в различных режимах работы электрической машины при эксплуатации или найдены путем разложения кривой выходного напряжения в ряд Фурье[4].

СПИСОК ЛИТЕРАТУРЫ

1 Карташев И.И., Тульский, В.Н., Шамонов Р.Г. Управление качеством электроэнергии.– М.: Издательский дом МЭИ, 2006.– С. 242-245.

2 Гамазин, С.И., Ставцев В.А., Цырук С.А. Переходные процессы в системах промышленного электроснабжения, обусловленные электродвигательной нагрузкой.– М.: Издательство МЭИ, 1997.– С. 70-77.

3 Шабанов, В.А., Кабаргина, О.В. Перспективы использования частотно-регулируемого электропривода магистральных насосов на НПС: монография.– Уфа: Изд-во УГНТУ, 2010.– С. 6-26.

4 Ярулин, Д.Е. Учет влияния высших гармоник на выходе многоуровневого преобразователя частоты на электродвигатель СТД-8000: сборник научных трудов.-63-я научно-техническая конференция студентов, аспирантов и молодых ученых УГНТУ.- Уфа: Изд-во УГНТУ, 2012.

УДК 621.316