Общая задача линейного программировании (лп). Матричная форма задачи лп. Графический метод решения задачи лп.
Задачи линейного программирования охватывают самые разнообразные управленческие ситуации, требующие расчета оптимальных решений. Наряду с различными моделями производственных ситуаций они содержат задачи, возникающие из других экономических проблем. Единый подход к моделированию разнообразных задач позволяет разработать единые методы их решения и анализа, дает возможность увидеть существенные общие черты в проблемах, различных по экономическому содержанию и источникам возникновения. Дадим необходимые определения.
Функция n переменных x1, x2,
... xn
называется
линейной функцией, если она
представима в виде линейной комбинации
переменных, то есть в виде суммы переменных
с постоянными коэффициентами
Задачей линейного программирования
называется задача, состоящая в
нахождении экстремального (максимального
или минимального) значения линейной
функции (выручки)
при
условии, что переменные удовлетворяют
системе линейных равенств и неравенств:
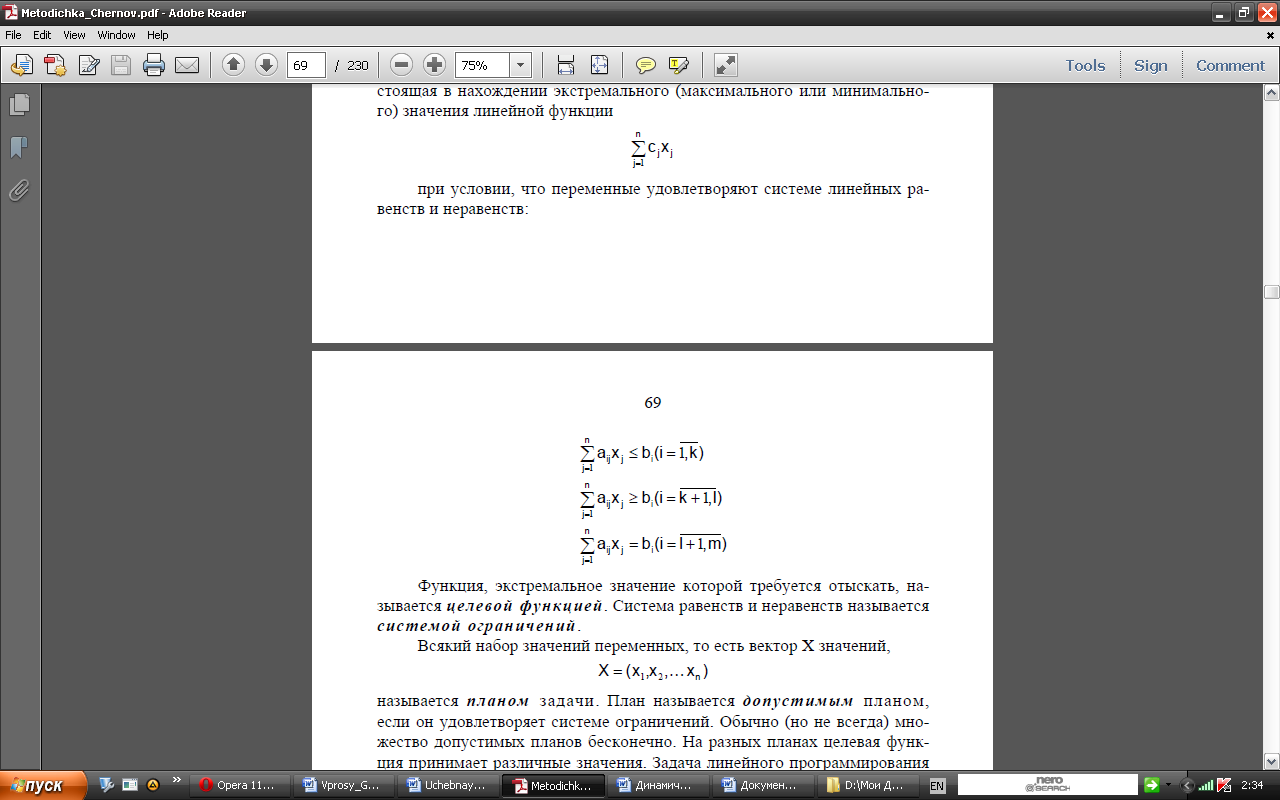
Функция, экстремальное значение которой требуется отыскать, называется целевой функцией. Система равенств и неравенств называется системой ограничений. Всякий набор значений переменных, то есть вектор X значений, X= (x1 ,x2…xn) называется планом задачи. План называется допустимым планом, если он удовлетворяет системе ограничений. Обычно (но не всегда) множество допустимых планов бесконечно. На разных планах целевая функция принимает различные значения. Задача линейного программирования требует, чтобы среди всех допустимых планов был найден тот план, на котором целевая функция достигает искомого экстремального значения (максимального и минимального, в зависимости от конкретной задачи). Такой план называется оптимальным планом. Значение целевой функции на оптимальном плане называется оптимумом. Решить задачу линейного программирования – значит найти ее оптимальный план и оптимум.
Матричная форма записи задачи линейного программирования
З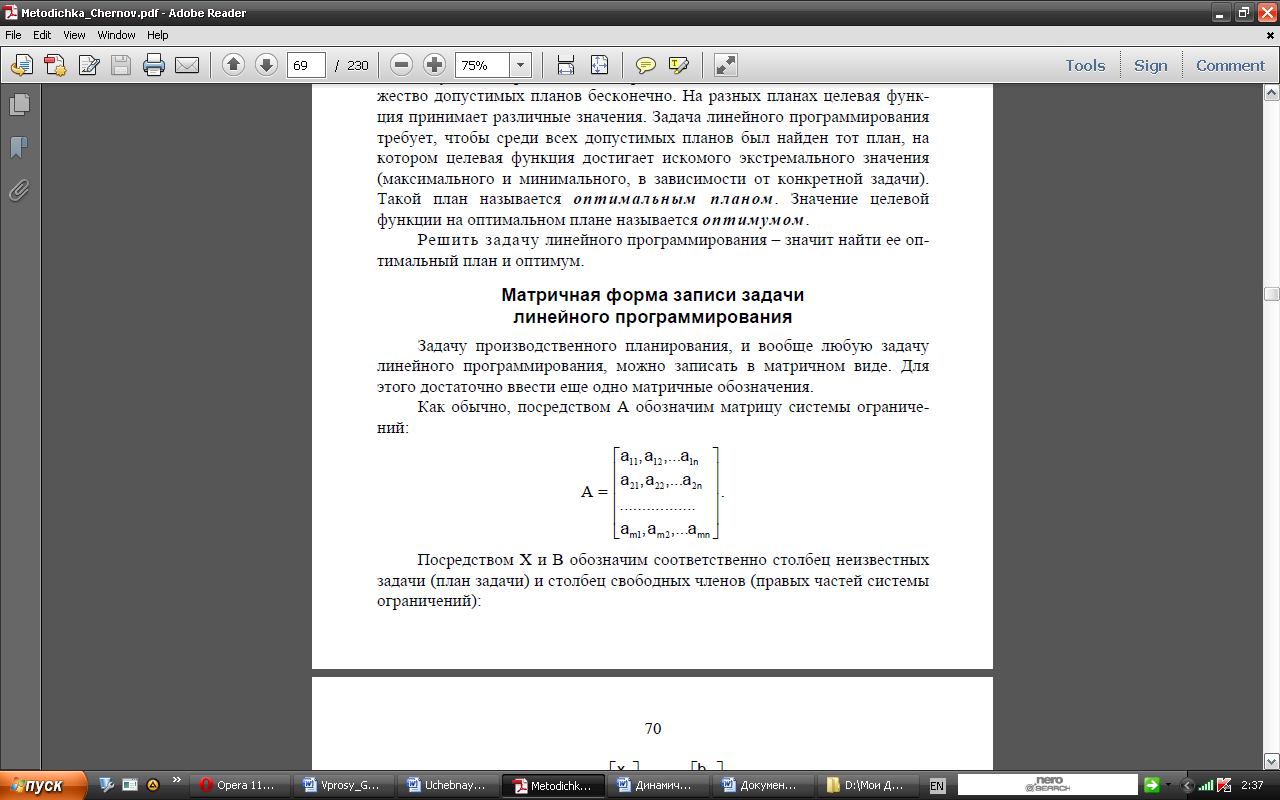
адачу
производственного планирования, и
вообще любую задачу линейного
программирования, можно записать в
матричном виде. Для этого достаточно
ввести еще одно матричные обозначения.
Посредством расхода ресурсов (A) обозначим
матрицу системы ограничений:
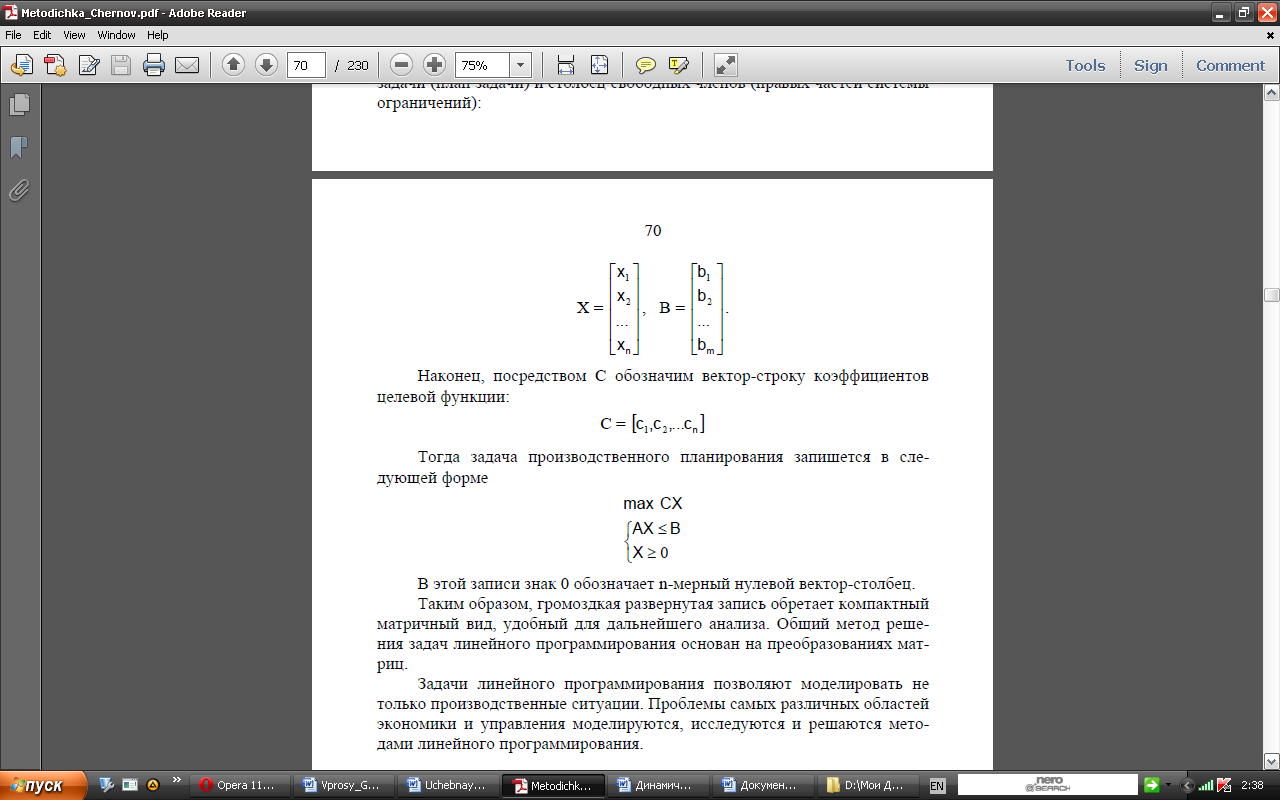
Посредством X (кол-во продукции) и B (запасы) обозначим соответственно столбец неизвестных задачи (план задачи) и столбец свободных членов (правых частей системы ограничений):
.
Наконец, посредством C обозначим вектор-строку коэффициентов целевой функции:
C = [c1 ,c2 ..cn ]
Задача производственного планирования:
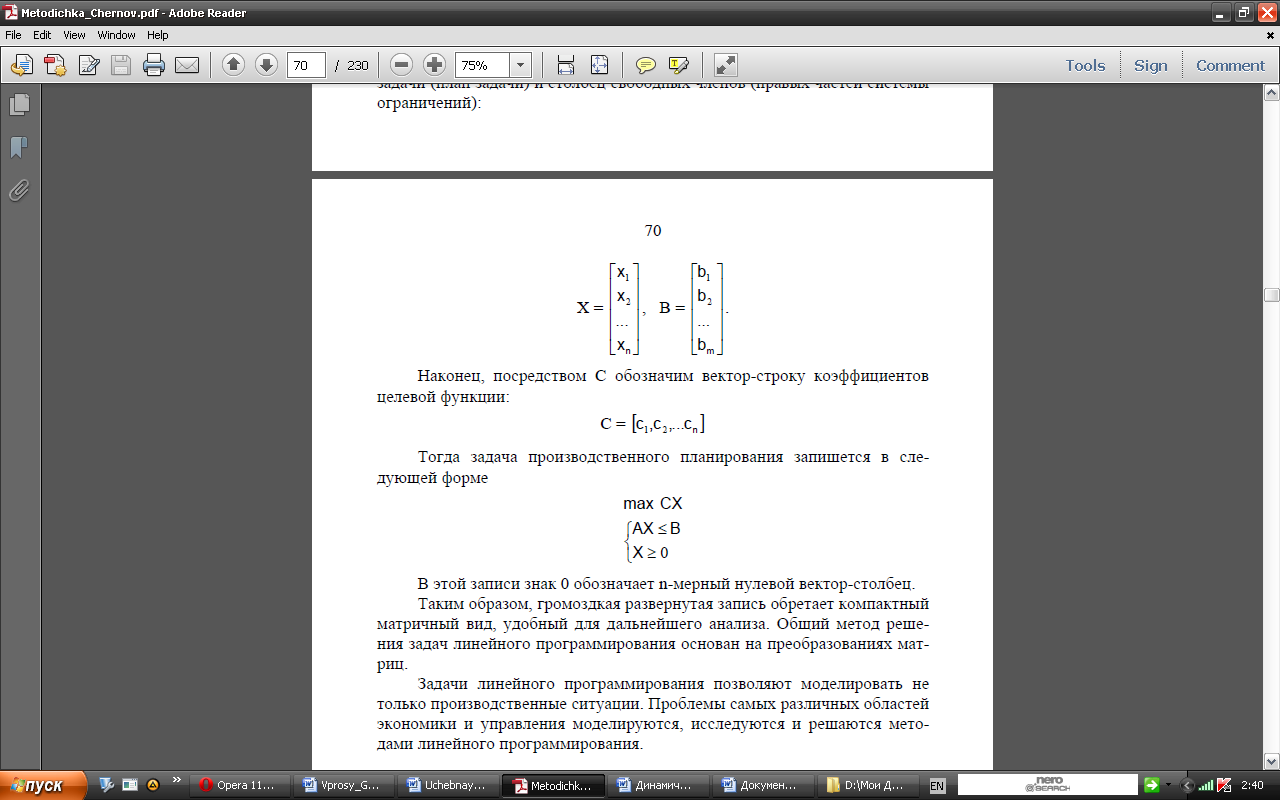
В этой записи знак 0 обозначает n-мерный нулевой вектор-столбец.Таким образом, громоздкая развернутая запись обретает компактный матричный вид, удобный для дальнейшего анализа. Общий метод решения задач линейного программирования основан на преобразованиях матриц.
Задачи линейного программирования позволяют моделировать не только производственные ситуации. Проблемы самых различных областей экономики и управления моделируются, исследуются и решаются методами линейного программирования.
Графический метод решения задачи ЛП.
1.Построение области допустимых планов.
Сначала изобразим границу полуплоскости, соответствующую множеству решений неравенств. Для этого неравенства заменим равенствами. Множество решений этих уравнений соответствует прямой на координатной плоскости. Эти прямые делят координатную плоскость на две полуплоскости. Для определения полуплоскости, соответствующей множеству решений неравенств, выберем точку, не лежащую на граничной прямой (например, начало координат), и подставим ее координаты в наши неравенства.
Пересечение всех полученных полуплоскостей определяет шестиугольник, примыкающий к началу координат. Это и есть область допустимых планов.
Любая точка данного шестиугольника удовлетворяет всем ограничениям задачи и соответствует допустимому плану. Если при этом точка лежит на стороне шестиугольника, то ее координаты, подставленные в левую часть ограничения-неравенства, обращают ограничение в равенство. Такое ограничение называется связанным. Данная ситуация означает, что реализация плана требует полного использования соответствующего ресурса.
Точка, лежащая в вершине шестиугольника, обращает в равенство сразу два ограничения и соответствует полному использованию сразу двух ресурсов. Точка, лежащая вне шестиугольника, не удовлетворяет хотя бы одному ограничению. Графики позволяют не просто констатировать недопустимость такой внешней точки, но и определить, каким именно ограничениям она не удовлетворяет, каких именно ресурсов не хватает для реализации плана. Построение области допустимых планов использует лишь систему ограничений. Для определения оптимального плана необходимо привлечь целевую функцию. Однако кое-что про оптимальный план можно сказать уже сейчас. Во-первых, область допустимых планов непуста и ограничена. Следовательно, оптимальный план существует. Во-вторых, оптимальный планом наверняка окажется одна из вершин шестиугольника. Если оптимальный план у нашей задачи единствен, то этим планом будет одна вершина. Если же он не единствен, то этим оптимальным планом окажутся две соседние вершины, а вместе с ними и все точки стороны шестиугольника.
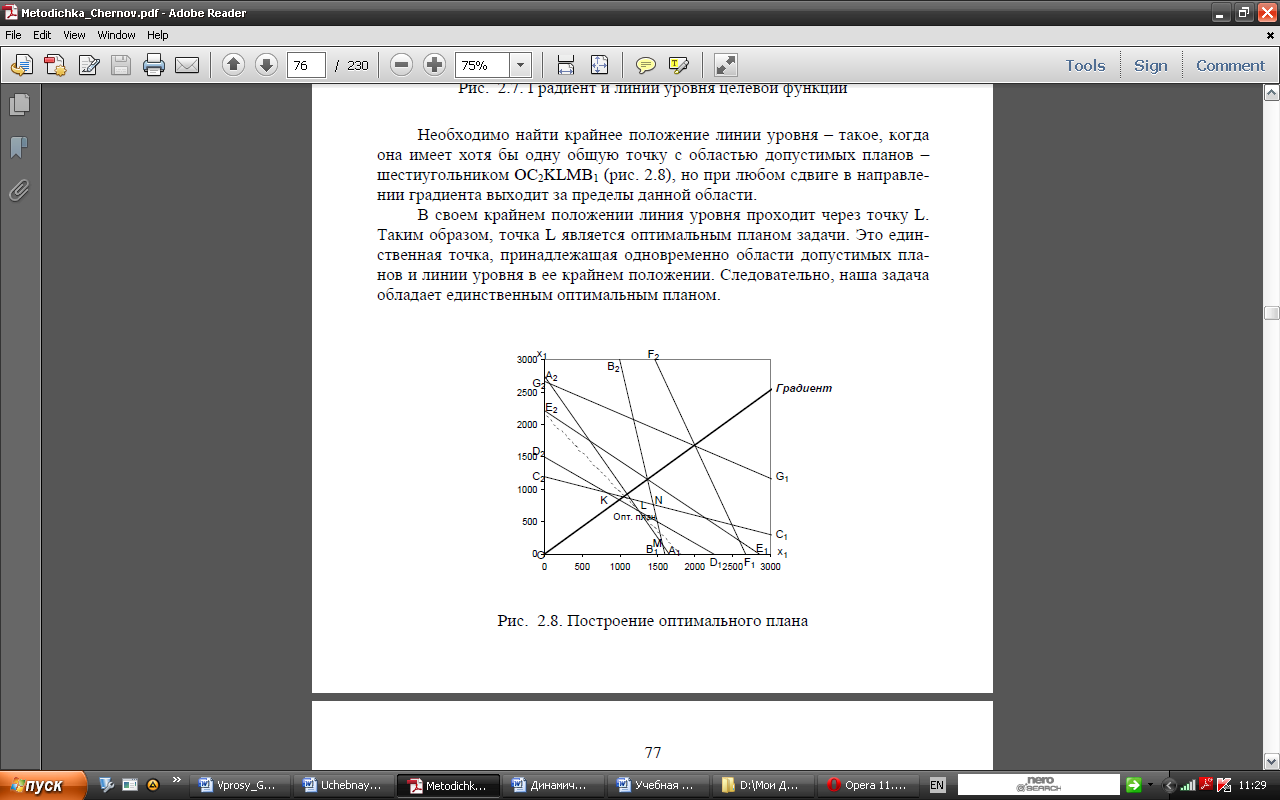
L –точка оптимального плана
A1A2, B1B2, C1C2,D1D2, E1E2, F1F2, G1G2 –линии ограничения ресурсов
Градиент – линия роста целевой функции
Пунктирная линия – целевая функция (проходит через точку L)