66. Логарифмические характеристики колебательного звена

Для колебательного звена частотная функция может быть записана в виде

. (11.8)

Логарифмируя выражение (11.8), найдем

(11.9)

и

(11.10)

Используя формулы (11.9) и (11.10), можно найти вид логарифмических характеристик колебательного звена. Делая допущения, аналогичные тем, которые име­ли место при нахождении приближенной характеристики инерционного звена, и приняв , можно построить приближенные логарифмические амплитудные и фазовые характеристики колебательного звена. Для построения приближенной амплитудной характеристики нужно най­ти значение , затем провести прямую, парал­лельную оси частот и отстоящую от нее на величину 20lgk, до точки с частотой и, наконец, из этой точки провести прямую с наклоном —40 дб/дек (или —12 дб/окт). Такое построение приведено на рисунке 11.4,а.

Приближенная фазовая характеристика может быть построена по следующим формулам (дающим ошибку не более 2°)

для T1ω<0,4

(11.11)

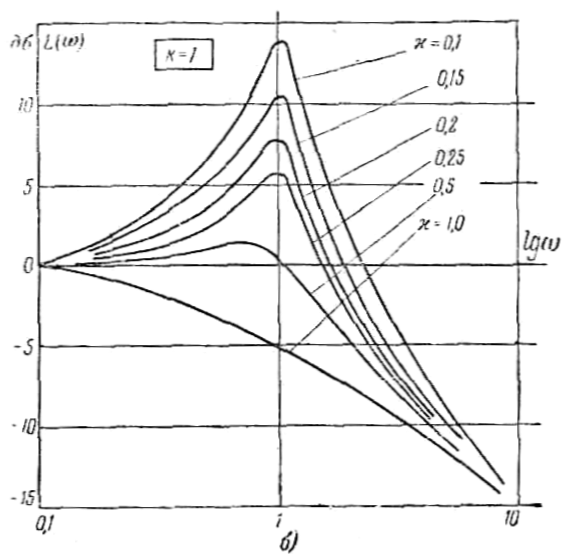
Однако следует учитывать, что построение приближен­ной логарифмической амплитудной характеристики ко­лебательного звена связано с наличием существенной погрешности, зависящей от коэффициента затухания . При χ= 0,5 ошибка минимальна. При условии 0,4≤х≤0,7 ошибка не превышает 3 дб.

Вид реальных логарифмических амплитудных L(ω) и фазовых характеристик для колебательного звена приведен на рисунке 11.4,б и в.

Рисунок 11.4 - Приближенные (а) и реальные (б и в) логарифмические

характеристики колебательного звена.

67.Построение амплитудных и фазовых логарифмических характеристик системы, логарифмический критерии устойчивости.

При построении логарифмических амплитудных и фа­зовых характеристик системы можно руководствоваться следующими соображениями.

Обычно передаточная функция системы в общем ви­де (без запаздывающих звеньев) имеет следующий вид

(12.1)

Делая в этом выражении подстановку и на­ходя модуль |К(j)|, можно записать

(12.2)

Для построения суммарной логарифмической амплитуд­ной частотной характеристики можно построить ЛАЧХ типовых звеньев и затем в соответствии с общим выра­жением для L() просуммировать их с соответствующи­ми знаками. Однако проще поступить несколько иначе, порядок такого построения рассмотрим на следующем частном примере.

Пусть система имеет в разомкнутом состоянии ча­стотную функцию следующего вида

(12.3)

согласно сказанному можем записать

(12.4)

Предположив для определенности T1>T2>T3 и обозначив сопрягающие частоты нане­сем на оси абсцисс их, а также частоту =1 (рисунок 12.1) и отложим в выбранном масштабе величину 20lgk. При частоте (<1) все слагаемые, кроме , могут не учитываться ввиду их малой величины. Поэтому в интер­вале 0<<1 вычерчивается прямая АБ с наклоном 20 дб/дек. При частотах, лежащих в интервале 1<<2, должен учитываться член +20lg|T1j+1|, в результате чего получается прямая БВ, параллельная оси абсцисс. При 2<<3 должен быть учтен член —20lg|T2j+1|, поэтому логарифмическая характеристика в этом интер­вале частот будет изображаться прямой ВГ с наклоном - 20 дб/дек.При частотах  больших, чем 3, необхо­димо в частотной функции системы учитывать все сла­гаемые, т. е. и

Рисунок 12.1 - Пример построения амплитудной лога­рифмической характеристики системы

член —20lg|T3j+1|,; и суммарная кривая в этом случае может быть изображена отрезком ГД с наклоном - 40 дб/дек. Таким образом, общий вид при­ближенной амплитудной логарифмической характеристи­ки рассматриваемой системы с достаточной степенью точности может быть изображен ломаной линией АБВГД. Построение фазовой логарифмической характеристи­ки системы, соответствующей записанному выше выра­жению для передаточной функции этой системы, можно произвести согласно следующему выражению

(12.5)

Из приведенного выражения следует, что для построения ЛФЧХ системы нужно сложить с соответствующими зна­ками ЛФЧХ отдельные звенья системы.

Такое построение для системы с передаточной функ­цией, аналогичной функции предыдущего примера, но при T1<T2<Tз приведено на рисунке 12.2. Частоты сопря­жения 1,2,3 получены в соответствии со значениями постоянных времени. Для интегрирующего звена фазо­вая характеристика изображена прямой 1, для двух инерционных звеньев - кососимметричными кривыми 2 и 3, а для дифференцирующего звена - кососимметричной кривой 4. Суммарная фазовая характеристика изо­бражена кривой 5.

Рисунок 12.2 - Пример построения фазовой ча­стотной характеристики системы