В массиве грунта от действия полосовой нагрузки

Построить эпюры вертикальных сжимающих напряжений в массиве грунта от действия полосовой нагрузки р, изменяющейся по закону прямой в точках на заданной вертикали и горизонтали, расположенной на расстоянии z от поверхности (рис. 4.1). Точки по вертикали на глубине 0, 1, 2, 4 и 6 м, по горизонтали на границах и в середине треугольной и равномерно распределенной нагрузок.

Исходные данные – по табл. 4.1.

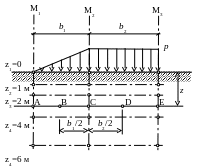
Рис. 4.1. Схема к задаче 4

Таблица 4.1. Исходные данные к задаче 4

Вариант	b1, м	b2, м	z, м	p, кПа	Расчетная вертикаль
1	2	2	1	150	М1
2	2	2	1	200	M2
3	2	2	2	250	МЗ
4	2	4	2	300	М1
5	2	4	2	350	М2
6	2	4	1	400	М3
7	4	2	1	150	М1
8	4	2	2	200	М2
9	4	2	2	250	М3
10	4	4	1	300	М1
11	4	4	1	350	М2
12	4	4	1	400	М3
13	4	8	2	150	М1
14	4	8	2	200	М2
15	4	8	4	250	М3
16	8	4	4	300	М1
17	8	4	2	350	М2
18	8	4	2	400	М3
19	8	8	4	150	М1
20	8	8	4	200	М2
21	8	8	2	250	М3
22	8	16	2	300	М1
23	8	16	2	350	М2
24	8	16	2	400	М3
25	8	12	2	250	М2

Пример

Построить эпюры вертикальных сжимающих напряжений в массиве грунта от действия полосовой нагрузки p =200 кПа, изменяющейся по закону прямой в точках на заданной вертикали и горизонтали, расположенной на расстоянии z =2 м от поверхности (рис. 4.2). Ширина треугольной нагрузки b₁ = 2 м, ширина прямоугольной нагрузки b₂ = 2 м. Точки по вертикали M₃ на глубине 0, 1, 2, 4 и 6 м, по горизонтали на границах и в середине треугольной и прямоугольной нагрузок.

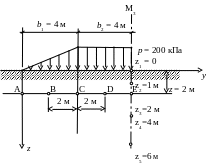
Рис. 4.2. Схема расположения нагрузок и точек определения

вертикальных сжимающих напряжений

Решение

Примем координатную систему yz.

Для распределенной полосовой нагрузки шириной b, изменяющейся по закону треугольника, вертикальные напряжения в грунтовом массиве определяются по формуле

,

где K_z – коэффициент, зависящий от соотношений z/b и y/b и определяемый по [4], y – горизонтальная координата рассматриваемой точки от оси, проходящей через вершину треугольной нагрузки; z – вертикальная координата точки от ограничивающей плоскости.

Для равномерно распределенной полосовой нагрузки шириной b вертикальные напряжения в грунтовом массиве определяются по той же формуле, что и для треугольной, но горизонтальная координата y отсчитывается от оси симметрии прямоугольной нагрузки.

Вертикальные сжимающие напряжения от совместного действия треугольной и прямоугольной нагрузок определяются суммированием напряжений от соответствующих нагрузок.

Определим напряжения по вертикали М₃.

Для точки, находящейся на глубине z₁=0, отношения ; для треугольной нагрузки; ; для прямоугольной нагрузки. Значения коэффициентов K_z будут следующими: K_z1 = 0; K_z2 = 0,5.

Напряжение от совместного действия треугольной и прямоугольной нагрузок

Для точки, находящейся на глубине z₂=1 м, отношения ; ; ; . Значения коэффициентов: K_z1 = 0,003; K_z2 = 0,5.

Напряжение

Для точки, находящейся на глубине z₃=2 м, отношения ; ; ; . Значения коэффициентов: K_z1 = 0,017; K_z2 = 0,48.

Напряжение

Для точки, находящейся на глубине z₄=4 м, отношения ; ; ; . Значения коэффициентов: K_z1 = 0,045; K_z2 = 0,41.

Напряжение

Для точки, находящейся на глубине z₅=6 м, отношения ; ; ; . Значения коэффициентов: K_z1 = 0,062; K_z2 = 0,33.

Напряжение

Определим напряжения на горизонтальной прямой в точках A, В, С, D на глубине z =2 м.

Для точки А отношения ; ; ; . Значения коэффициентов: K_z1 = 0,127; K_z2 = 0,02.

Напряжение

Для точки B отношения ; ; ; . Значения коэффициентов: K_z1 = 0,41; K_z2 = 0,08.

Напряжение

Для точки C отношения ; ; ; . Значения коэффициентов: K_z1 = 0,353; K_z2 = 0,48.

Напряжение

Для точки D отношения ; ; ; . Значения коэффициентов: K_z1 = 0,056; K_z2 = 0,82.

Напряжение

Для точки E напряжения

П остроим эпюры вертикальных напряжений, откладывая ординаты соответствующих значений в расчетных точках по вертикали и горизонтали ( рис 4.3).

Рис. 4.3. Эпюры вертикальных сжимающих напряжений по горизонтальному и вертикальному сечениям

Задание 5. Определение устойчивости откоса методом

круглоцилиндрических поверхностей скольжения

Определить коэффициент устойчивости откоса, сложенного однородным грунтом с характеристиками , , с при заданном положении кривой скольжения в виде дуги окружности с центром в т. О₁.

Крутизна откоса 1:m, где ; откос нагружен равномерно распределенной нагрузкой q.

Исходные данные – по табл. 5.1.

Рис. 5.1. Схема к задаче 5

Таблица 5.1. Исходные данные к задаче 5

Вариант	Высота откоса H, м	h, м	m	q, кПа	, кН/м3	, °	с, кПа
1	4,2	11	1,1	10	15,6	34	10
2	4,4	10,6	1,2	12	16	34	12
3	4,6	10,3	1,3	14	16,5	32	14
4	4,8	10,0	1,4	16	17	32	18
5	5,0	9,8	1,5	18	17,5	30	20
6	5,2	9,6	1,6	20	18	30	22
7	5,4	9,4	1,7	22	18,5	28	24
8	5,6	9,2	1,8	24	19	28	26
9	5,8	9,0	1,9	27	19,5	26	28
10	6,0	8,8	2,0	30	20	26	30
11	4,1	11	1,1	10	20,5	26	30
12	4,3	10,7	1,2	12	19,8	26	28
13	4,5	10,4	1,3	14	19,3	28	26
14	4,7	10,1	1,4	16	18,7	28	24
15	4,9	9,8	1,5	18	18,2	30	22
16	5,1	9,6	1,6	20	17,8	30	20
17	5,3	9,4	1,7	22	17,3	32	18
18	5,5	9,2	1,8	24	16,5	32	14
19	5,7	9,0	1,9	27	16,2	34	12
20	5,9	8,8	2,0	30	15,8	34	10
21	4,2	11	1,0	10	16	34	12
22	4,6	10,4	1,2	14	17	32	18
23	5,0	9,8	1,4	18	18	30	22
24	5,4	9,4	1,6	22	19	28	26
25	5,8	9,0	1,9	27	20	26	30

Пример

О ткос сложен однородным грунтом с характеристиками: γ = 17,5 кН/м³, φ=30 ^°, с = 20 кПа. Высота откоса Н=4,4 м, крутизна l:m, где m = 1,1. На поверхности откоса приложена равномерно распределенная нагрузка q = 12 кПа. Определить коэффициент устойчивости откоса для h = 10,7 м. (рис. 5.2).

Рис. 5.2. Схема откоса и положение дуги скольжения

Решение

Примем координатную систему xz; радиусом R=(h+H), проводим дугу окружности, выделив массив грунта DAB (рис. 5.3)

Координаты точек: О₁ (0;-10,7); D (0;4,4); А (mH;0) или А (4,84;0).

Из Δ ОО₁В имеем , откуда

.

Тогда , а т. В имеет координаты (10,65;0).

Рис. 5.3. Схема деления массива на отсеки

Решение проводим по алгоритму:

1. Делим массив DAB на 6 отсеков, нумеруя их снизу вверх: b₁= b₂=1,6 м; b₃=1,64 м; b₄= b₅=1,9 м; b₆=2,01 м.

2. Записываем уравнение окружности с центром в т. О₁ (0;-10,7)

x²+(z+10,7)²=R² или x²+z²+21,4z – 113,52=0.

3. Вычисляем правые высоты отсеков.

Для отсека №1, используя уравнение окружности, при x₁=1,6 м, получаем z₁=4,32 м. Тогда

Аналогично для отсека № 2 при x₂=3,2 м получаем z₂=4,06. Правая высота отсека

Для отсека №3 x₃=4,84 м, z₃=3,6 м и

Для 4 – 6 отсеков соответственно имеем:

x₄=6,74 м, z₄ = h₄=2,81 м;

x₅=8,64 м, z₅ = h₅ =1,68 м;

x₆=10,65 м, z₆ = h₅ = 0 м.

4. Определяем площади отсеков, пренебрегая кривизной поверхности скольжения в силу незначительной разницы в длине между хордой и дугой в пределах одного отсека:

; ; ; ;

; .

5. Определяем вес отсеков (l = 1 м); для № 4, № 5 и № 6 учитываем действие нагрузки q = 12 кПа:

Q₁=S₁ = 1·17,5=19,25 кН/м;

Q₂ = S₂ = 3,15·17,5=55,13 кН/м;

Q₃ = S₃ = 5,06·17,5=88,55 кН/м;

Q₄ = S₄ +qb₄ = 6,09·17,5+12·1,9=129,38 кН/м;

Q₅ = S₅ +qb₅ = 4,27·17,5+12·1,9=97,53 кН/м;

Q₆ = S₆ +qb₆ =1,69·17,5+12·2,01=53,70 кН/м.

Равнодействующие Q_i считаем приложенными в точках пересечения соответствующего участка дуги скольжения и вертикальной линии, проходящей через центр тяжести отсека, т.е. в точках с абсциссами:

; ;

;

;

;

.

6. Определяем центральные углы _i между вертикалью и радиусом в точке приложения веса отсека по формуле :

; ; ; ; ; .

7. Центральный угол, соответствующий дуге DB:

.

Длина дуги кривой скольжения определяется из соотношения

.

Силы Q_i раскладываем на две составляющие: нормальную N_i к заданной поверхности и касательную T_i, учитывая также сцепление грунта по всей поверхности скольжения. Составляем таблицу для расчета коэффициента устойчивости.

Таблица 5.2. Определение составляющих сил от веса отсеков

№	Qi	i	sini	cosi	Ti =Qi sini	Ni =Qi cosi
1	19,25	4,1	0,071	0,997	1,37	19,19
2	55,13	9,5	0,165	0,986	9,1	54,36
3	88,55	15,6	0,269	0,963	23,82	85,27
4	129,38	22,4	0,381	0,925	49,29	119,68
5	97,59	30,3	0,505	0,863	49,28	84,22
6	53,70	38,1	0,617	0,787	33,13	42,26

Рассчитываем коэффициент устойчивости для принятого очертания поверхности скольжения как отношение момента удерживающих сил (к которым относится сила трения и сцепление) к моменту сил сдвигающих (касательная составляющая веса отсеков):

.

Вывод. Для заданного положения поверхности скольжения откос устойчив, т. к. K_уст=2,83 > 1.

На практике условие устойчивости должно выполняться для минимального значения коэффициента устойчивости, рассчитанного для наиболее опасной возможной поверхности скольжения.

Задание 6. Определение активного и пассивного давлений грунта

на подпорную стенку

Построить эпюры активного и пассивного давлений грунта на подпорную стенку с гладкими вертикальными гранями и горизонтальной поверхности засыпки (рис 6.1). Определить равнодействующие давлений, указать точки их приложения и ширину призм обрушения и выпора.

Исходные данные – по табл. 6.1.

q

H

d

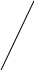
Рис 6.1. Схема к задаче 4

Таблица 6.1. Исходные данные к задаче 6

Вариант	Размеры подпорной стенки, м		Нагрузка q, кПа	Характеристики грунта засыпки
	H	d		, кН/м3	,	с, кПа
1	2	3	4	5	6	7
1	4,5	1,5	20	17,2	17	10
2	4,8	1,6	25	17,7	19	9
3	5,0	1,7	30	18,2	21	8
4	5,4	1,8	35	19	23	7
5	5,7	1,9	40	18,5	25	6
6	6,0	2,0	42	18,0	27	5
7	6,2	2,1	45	17,5	29	4
8	6,4	2,2	48	17,0	31	3
9	6,7	2,3	50	16,5	33	2
10	7,0	2,4	55	16,0	35	1
11	4,5	1,5	15	17,2	18	10
12	4,8	1,6	17	17,7	20	9
13	5,0	1,7	22	18,2	22	8
14	5,4	1,8	27	19	24	7
15	5,7	1,9	32	18,5	25	6
16	6,0	2,0	34	18,0	28	5
17	6,2	2,1	37	17,5	30	4
18	6,4	2,2	39	17,0	32	3
19	6,7	2,3	41	16,5	34	2
Продолжение табл. 6.1
1	2	3	4	5	6	7
20	7,0	2,4	44	16,0	36	1
21	4,5	1,5	20	16,5	34	2
22	5,0	1,7	30	17,5	30	4
23	5,7	1,9	40	18,5	25	6
24	6,2	2,1	45	18,2	22	8
25	6,7	2,3	50	17,2	18	10

Пример

Грунт имеет характеристики: γ = 18,5 кН/м³, φ=25 ^°, с = 6 кПа. Передняя и задняя грани стенки гладкие вертикальные. Высота задней грани Н=4,7 м, передней – d=1,6 м. На горизонтальной поверхности засыпки приложена равномерно распределенная нагрузка q = 25 кПа. Построить эпюры активного и пассивного давлений грунта на подпорную стенку и определить равнодействующие давлений, указав точки их приложения и ширину призм обрушения и выпора (рис. 6.2).

Рис 6.2. Схема подпорной стенки

Решение

Подпорная стенка, поддерживая грунт от обрушения, испытывает с его стороны давление, которое принято называть активным. Активное давление, воздействуя на стенку, вызывает ее смещение, что приводит к возникновению сопротивления грунта с другой стороны. Это сопротивление называется пассивным давлением. В первом случае вертикальное напряжение _z = ₁ = max, а горизонтальное напряжение _x = _a = min– активное давление, во втором _z = ₃ = min, а _x = _p = max – пассивное давление.

Активное давление грунта на абсолютно гладкую (отсутствует трение) подпорную стенку без учета сцепления грунта определяется по формуле

,

где  - удельный вес грунта; z – глубина точки, в которой определяется давление; – коэффициент активного давления:

.

Активное давление грунта на нижней грани подпорной стенки, т.е. на глубине z = H:

σ_a = γ·H·λ_а = 18,5·4,7·0,41 = 35,65 кПа.

Наличие сцепления уменьшает активное давления на величину

.

В этом случае эпюра активного давления начинается на глубине

При действии по поверхности засыпки сплошной равномерно распределённой нагрузки q активное давление грунта

.

Равнодействующая активного давления

Равнодействующая от давления приложена в центре тяжести эпюры , т.е. на расстоянии H/3 = 1,57 м, равнодействующая от давления _qa – на расстоянии H/2 = 2,35 м от нижней грани подпорной стенки.

Пассивное давление на нижней грани подпорной стенки определяется по формуле:

,

где – коэффициент пассивного давления; .

;

;

.

Равнодействующая пассивного давления

.

Точка приложения пассивного давления находится на расстоянии от нижней грани подпорной стенки.

Определяем размеры призм обрушения и выпора:

,

.

Строим эпюры активного и пассивного давлений грунта на подпорную стенку.

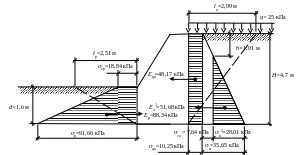
Рис 6.3. Эпюра активного и пассивного давлений грунта на подпорную стенку

Задание 7. Определение стабилизированной осадки основания

фундамента по схеме линейно-деформируемого полупространства

Фундамент с прямоугольной подошвой размерами b×l и глубиной заложения d передает на основание вертикальную нагрузку N_II. Основание сложено мощным слоем грунта с характеристиками _II, E,  (рис. 7.1). Определить стабилизированную осадку двумя способами:

1. По формуле Шлейхера;

2. Методом послойного суммирования.

Объяснить причины расхождения результатов.

И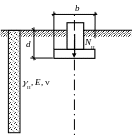 сходные данные – по табл. 7.1.

Рис. 7.1. Схема к задаче 7

Таблица 7.1. Исходные данные к задаче 7

Вариант	Размеры подошвы b×l, м	Глубина заложения d, м	Нагрузка на уровне подошвы NII, МН	Удельный вес грунта, II, кН/м3	Коэффициент Пуассона 	Модуль деформации E0, МПа
1	2×2	2,4	1,2	18,0	0,26	10
2	3×1,5	1,6	1,3	19,0	0,27	12
3	3×2,5	3,0	2,3	18,5	0,28	14
4	4×2	1,5	2,6	17,8	0,29	8
5	4×2,5	3,0	2,7	18,4	0,3	6
6	4×3	2,0	3,8	17,2	0,32	16
7	5×2	2,8	4,1	18,1	0,34	18
8	5×3	2,6	5,2	19,5	0,36	20
9	6×3	3,0	7,0	20,0	0,38	22
10	6×4	2,5	7,6	17,9	0,4	24
11	2×2	2,7	1,0	18,0	0,3	11
12	3×1,5	1,9	1,1	19,0	0,29	13
13	3×2,5	3,2	2,1	18,5	0,28	15
14	4×2	1,8	2,4	17,8	0,27	7
15	4×2,5	2,6	2,5	18,4	0,26	9
16	4×3	2,3	3,5	17,2	0,4	17
17	5×2	3,1	3,9	18,1	0,38	19
18	5×3	2,9	4,9	19,5	0,36	21
19	6×3	3,3	6,7	20,0	0,34	23
20	6×4	2,2	7,2	17,9	0,32	25
21	2×2	1,6	1,1	18,0	0,38	13
22	3×1,5	2,4	1,2	18,5	0,32	15
23	4×3	2,8	3,6	19,5	0,28	19
24	5×3	2,0	5,1	19,0	0,4	22
25	6×3	2,5	6,9	17,5	0,26	24

Пример

Фундамент с прямоугольной подошвой размерами 3×2м и глубиной заложения d = 2,5 м передает на основание вертикальную нагрузку N_II =1,9 МН. Основание сложено мощным слоем грунта с характеристиками: удельный вес грунта _II = 18,4 кН/м³, модуль деформации E = 6 МПа, коэффициент поперечной деформации =0,3. Определить стабилизированную осадку по формуле Шлейхера и методом послойного суммирования. Объяснить причины расхождения результатов.

Решение.

Формула Шлейхера для определения осадки поверхности линейно-деформируемого полупространства имеет вид

,

где  - коэффициент осадки, зависящий от формы площади загружения, жесткости фундамента и места расположения точки поверхности грунта и принимаемый по [3]; p₀ – дополнительное среднее давление под подошвой штампа.

Для абсолютно жесткого прямоугольного фундамента при отношении определяем по [3]  =1,05.

Дополнительное давление

Осадка методом послойного суммирования определяется по формуле

,

где  - безразмерный коэффициент, принимаемый равным 0,8; n – число слоев грунта в пределах сжимаемой тощи; h_i – толщина i - го слоя; h_i  0,4b; _zp,i – среднее вертикальное напряжение, возникающее в i - м слое; модуль деформации грунта i - го слоя.

Для расчета осадки строим эпюры вертикальных напряжений от собственного веса грунта и дополнительных напряжений по оси фундамента по формулам

,

,

где _i – удельный вес i - го слоя;  - коэффициент, принимаемый в зависимости от величин  = l/b и  = 2z/b по СНиП [2].

Сжимаемую толщу ограничивают глубиной, на которой дополнительное напряжение не более 20 % природного напряжения

.

Толщина расчетного слоя грунта h_i = 0,42=0,8 м.

Результаты расчета сводим в таблицу.

Таблица 7.2. Определение дополнительных и природных напряжений

z, м	 = 2z/b		zp, кПа	zg, кПа
1	2	3	4	5
0	0	1,0	270,67	46
0,8	0,8	0,853	230,88	60,72
1,6	1,6	0,544	147,24	75,44
2,4	2,4	0,337	91,22	90,16
Продолжение табл. 7.2
1	2	3	4	5
3,2	3,2	0,220	59,55	104,88
4,0	4,0	0,153	41,41	119,60
4,8	4,8	0,111	30,04	134,32
5,6	5,6	0,086	23,28	149,04

Строим эпюры вертикальных напряжений от собственного веса грунта и дополнительных напряжений (рис. 7.2).

Рис. 7.2. Эпюры вертикальных напряжений от собственного веса грунта

и дополнительных напряжений

Поскольку в формуле для осадки под знаком суммы переменной является только величина , то

.

равна сумме напряжений на границах всех средних слоев плюс половина напряжений на верхней и нижней границах сжимаемой толщи:

Отсюда осадка по методу послойного суммирования

Задание 8. Определение стабилизированной осадки и расчет затухания

осадки во времени абсолютно жесткого фундамента

Определить методом эквивалентного слоя полную стабилизированную осадку жесткого прямоугольного фундамента с размерами b×l при дополнительном давлении под подошвой p₀. Рассчитать во времени затухание осадки фундамента, возводимого на двухслойном водонасыщенном основании со свойствами грунтов m_v1, k_ф1 и m_v2, k_ф2.

Исходные данные – по табл. 8.1.

Таблица 8.1. Исходные данные к задаче 8

Вариант	Размеры подошвы b×l, м	Дополнительное давление под подошвой p0, кПа	Мощность первого слоя h1, м	Коэффициент относительной сжимаемости 1-го слоя mv1, МПа-1	Коэффициент фильтрации 1-го слоя kф1, см/с	Коэффициент относительной сжимаемости 2-го слоя mv2, МПа-1	Коэффициент фильтрации 2-го слоя kф2, см/с
1	1,8×1,8	160	1,8	0,222	1,710-8	0,265	8,410-9
2	2×2	210	2,3	0,176	2,210-8	0,284	4,1310-9
3	2,2×2,2	210	2,8	0,139	1,310-8	0,215	4,610-9
4	2,5×2,5	260	2,7	0,095	6,410-8	0,196	3,210-9
5	3×2	230	2,9	0,087	2,310-8	0,147	3,810-9
6	3,2×3,2	180	2,4	0,148	1,410-7	0,258	5,610-8
7	3,5×1,75	170	3,2	0,076	2,410-8	0,381	1,810-9
8	3,6×2,4	190	3,1	0,065	1,210-8	0,124	2,510-9
9	4×2	280	3,7	0,115	2,510-8	0,267	1,810-9
10	5,6×2,8	220	3,8	0,115	5,110-8	0,245	6,910-9
11	1,8×1,8	180	3,1	0,087	2,310-8	0,147	3,810-9
12	2×2	230	2,9	0,095	6,410-8	0,196	3,210-9
13	2,2×2,2	240	3,0	0,139	1,310-8	0,215	4,610-9
14	2,5×2,5	270	2,5	0,176	2,210-8	0,284	4,1310-9
15	3×2	250	2,0	0,222	1,710-7	0,265	8,410-8
16	3,2×3,2	200	3,6	0,105	5,110-8	0,245	6,910-9
17	3,5×1,75	180	3,9	0,115	2,510-8	0,267	1,810-9
18	3,6×2,4	220	2,9	0,065	1,210-8	0,124	2,510-9
19	4×2	300	3,0	0,076	2,410-7	0,381	1,810-8
20	5,6×2,8	250	2,2	0,148	1,410-7	0,258	5,610-8
21	1,8×1,8	170	2,0	0,176	2,210-8	0,284	4,1310-9
22	2,2×2,2	230	2,4	0,095	6,410-8	0,196	3,210-9
23	3×2	240	2,7	0,148	1,410-7	0,258	5,610-8
24	3,5×1,75	190	3,0	0,065	1,210-8	0,124	2,510-9
25	4×2	290	3,3	0,115	5,110-8	0,245	6,910-9

Пример

Определить методом эквивалентного слоя полную стабилизированную осадку жесткого прямоугольного фундамента с размерами 3,8×1,9 м при дополнительном давлении под подошвой p₀ = 280 кПа (рис. 8.1). Рассчитать затухание осадки во времени. Основание сложено двумя слоями водонасыщенных грунтов. Первый слой грунта мощностью h₁ =3,9 м подстилается слоем грунта мощностью h₂ более 10 м. Коэффициенты относительной сжимаемости и фильтрации 1-го и 2-го слоев грунта соответственно равны: m_v1 =0,000105 кПа^-1, k_ф1 = 2,710^-8 см/сек; m_v2 = 0,000267 кПа^-1, k_ф2 = 1,610^-9 см/сек.

Рис. 8.1. Схема к задаче 8

Решение.

В соответствии с методом эквивалентного слоя полная стабилизированная осадка фундамента определяется по формуле

,

где m_vm – средний коэффициент сжимаемости грунта; h_э – мощность эквивалентного слоя, определяемая из выражения

,

где A - коэффициент эквивалентного слоя, зависящий от коэффициента Пуассона ₀, формы подошвы и жесткости фундамента и принимаемый по [4].

Величина среднего коэффициента относительной сжимаемости определяется в пределах сжимаемой толщи H = 2h_э из выражения

,

где n – число слоев грунта в пределах активной зоны; h_i – мощность i-го слоя грунта; m_vi – коэффициент сжимаемости i-го слоя; z_i - расстояние от нижней точки эквивалентной треугольной эпюры до середины слоя (рис. 8.2).

Примем значение коэффициента Пуассона грунтов ₀ = 0,3. По [4] для соотношения сторон  = l/b = 3,8/1,9 = 2 и ₀ = 0,3 найдем A = 1,49 и мощность эквивалентного слоя

.

Сжимаемая толща

.

Определим средний коэффициент относительной сжимаемости

Конечная осадка

.

Рис. 8.1. Расчетная схема по методу эквивалентного слоя

Затухание осадок во времени рассчитываем, используя осредненные характеристики слоистого основания, по формуле

,

где h – расчетная мощность уплотняемого слоя или длина пути фильтрации; – коэффициент консолидации; N – величина, принимаемая по [4] в зависимости от схемы загружения и степени консолидации U = S_t/S; k_фm – средний коэффициент фильтрации, определяемый по формуле

,

где k_фi – коэффициент фильтрации i-го слоя.

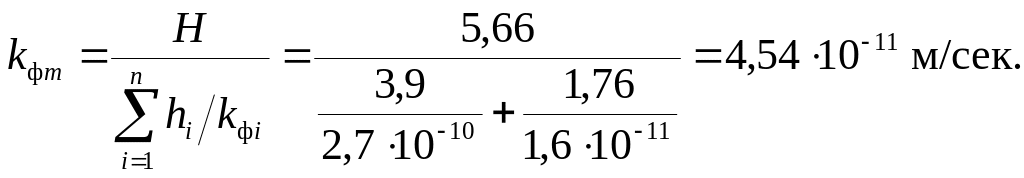
Расчетная схема расчета затухания осадок во времени соответствует случаю, когда водопроницаемость грунтов с увеличением глубины уменьшается, т.е. k_ф1 > k_ф2 (односторонняя фильтрация вверх), что соответствует случаю 2 (рис. 8.1).

Расчетная мощность уплотняемого слоя равна мощности активной зоны:

h = H = 2h_э = 5,66 м.

Время уплотнения от начала загружения, соответствующее заданной степени консолидации U,

Далее расчет ведем в табличной форме.

Таблица 8.2. Расчёт осадки во времени

Степень консолидации U	Параметр года	Параметр N (схема 2)	Время консолидации, год t = M  N	Осадка во времени, St = U  S, см (S = 9,7 см)
0		0	0	0
0,1		0,005	0,0544 года=20 дней	0,97
0,2		0,02	0,22 года=79,4 дней=2,6 мес	1,94
0,3		0,06	0,65 года=7,9 мес	2,91
0,4	10,88	0,13	1,41 года=1 год 5 мес	3,88
0,5		0,24	2,61 года=2 года 7,4 мес	4,85
0,6		0,42	4,56 года=4 года 7 мес	5,82
0,7		0,69	7,5 года=7 лет 6 мес	6,79
0,8		1,08	11,75 года=11 лет 9 мес	7,76
0,9		1,77	19,26 года=19 лет 3 мес	8,73
0,95		2,54	27,64 года=27 лет 8 мес	9,22

График затухания осадки во времени приведен на рис. 8.2.

Рис. 8.2. График изменения осадки во времени