5. Застосування степеневих рядів до наближених обчислень

Розвинення функцій у ряди Тейлора дає змогу у багатьох випадках обчислювати з великою точністю значення цих функцій, визначені інтеграли, границі, розв’язувати диференціальні рівняння, обчислювати суми числових рядів. У таких обчисленнях зберігають перших членів ряду, а решту відкидають. Для оцінки похибки знайденого наближеного значення треба оцінити суму відкинутих членів, тобто залишок ряду . Доцільно оцінку здійснювати так: якщо ряд знакосталий, то залишок порівнюють з геометричним рядом, члени якого утворюють спадну геометричну прогресію, а якщо ряд знакопочережний і його члени задовольняють умови теореми Лейбніца, то використовують оцінку , де – перший з відкинутих членів ряду. Для наближених обчислень за допомогою рядів використовуватимемо розвинення елементарних функцій, які наведені в додатку 1.

1. Обчислення значень функцій

Якщо функція розвивається у степеневий ряд в околі точки , то для обчислення значень функції в цьому околі можна використати розвинення (18).

Приклад 24. Обчислити наближенно з точністю до .

Розв’язання. Представимо заданий вираз у вигляді і застосуємо формулу 4 додатку 1. Оскільки входить до області збіжності степеневого ряду , то при , , отримаємо

.

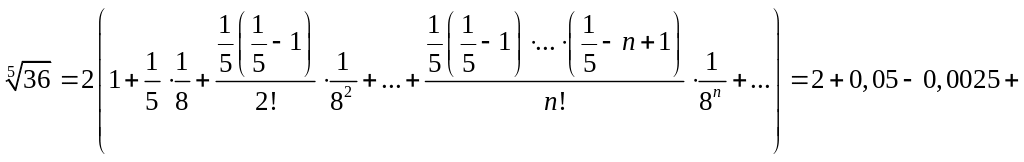
(Для забезпечення потрібної точності розрахунку необхідно взяти 4 члени, оскільки по наслідку з ознаки Лейбніца для збіжного знакопочережного ряду похибка ).

2. Обчислення інтегралів

Якщо має місце формула (18) і , то

,

де , і за цією формулою можна обчислити інтеграл з будь-якою точністю.

Приклад 25. Обчислити наближено інтеграл з точністю до .

Розв’язання. Використаємо розвинення в степеневий ряд функції за формулою 3 додатку А таблиці А, матимємо

Виразимо функцію через функціональний ряд:

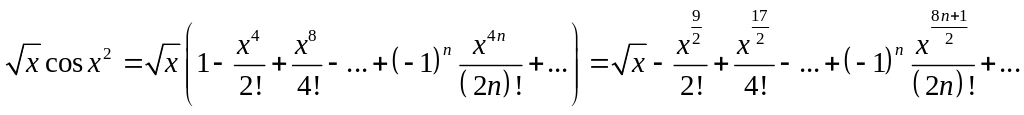
Оскільки областю збіжності даного ряду є інтервал і інтервал , то інтегруючи отриманий ряд почленно, знаходимо:

.

Отримали знакопочережний ряд, отже похибка при обчисленні суми не перевищує модуля першого відкинутого члену ряду. Знайдемо член ряду, величина якого менша за .

Отже, для досягнення необхідної точності потрібно відкинути член і всі наступні, тоді матимемо:

.

3. Інтегрування диференціальних рівнянь

Розв’язання деяких диференціальних рівнянь може бути представлене у вигляді степеневих рядів.

Метод розв’язання, при якому розв’язок рівняння записується рядом Маклорена, полягає в послідовному диференціюванні даного диференціального рівняння.

Приклад 26. Знайти перші чотири члена розвинення в ряд розв’язку рівняння , задовольняючого початковій умові .

Розв’язання. Шуканий розв’язок запишемо у вигляді ряду

Диференціюючи дане рівняння, знайдемо вираз для двох наступних похідних , :

; .

Обчислимо тепер значення похідних , , при , використовуючи початкові умови:

; ; .

Таким чином, розв’язання рівняння буде мати вигляд:

3. Обчислення границь

Користуючись відповідними розвиненнями у степеневі ряди, можна обчислювати границі, пов’язані з розкриттям невизначеностей виду .

Приклад 27. Знайти .

Розв’язання. Тут має місце невизначеність виду . Для її розкриття розвинемо функцію в ряд за формулою 9 додатку А таблиці А. Тоді отримаємо

.