2. Степеневі ряди. Теорема Абеля

Степеневий ряд – частковий випадок функціонального ряду. Він має вигляд

, (14)

де – коефіцієнти ряду.

При ряд приймає вигляд

. (15)

Теорема Абеля. Якщо степеневий ряд (15) є збіжним при деякому значенні , то він збіжний і притому абсолютно, при всіх значеннях , при яких . Якщо степеневий ряд є розбіжним при , то він є розбіжним при всіх значеннях , для яких .

Радіусом збіжності ряду (15) називається число таке, що при ряд збігається, а при розбігається. В цьому випадку кажуть про інтервал збіжності ряду ; на кінцях інтервалу при збіжність ряду потрібно визначати окремо, в залежності від виразу для .

Щоб знайти область збіжності степеневого ряду (15) потрібно спочатку визначити інтервал збіжності , а потім з’ясувати питання про збіжність ряду на границі інтервалу, тобто при і при .

Радіус збіжності можна дістати за однією з формул

, (16)

або

, (17)

якщо ці границі існують (скінченні або нескінченні).

Іноді краще знаходити інтервал збіжності, безпосередньо застосовуючи ознаки Д’Аламбера або Коші до ряду, утвореного з модулів членів ряду (15).

Приклад 17. Знайти радіус і інтервал збіжності степеневого ряду .

Розв’язання. Для даного ряду

, ;

при .

В силу ознаки Даламбера ряд є абсолютно збіжним при значеннях , що задовольняють нерівності

, або ,

яка рівносильна системі нерівностей

, або .

Таким чином, інтервал збіжності ряду , а радіус збіжності .

Приклад 18. Знайти область збіжності степеневого ряду .

Розв’язання. Спочатку виконаємо заміну , тоді матимемо .

Знаходимо радіус збіжності

.

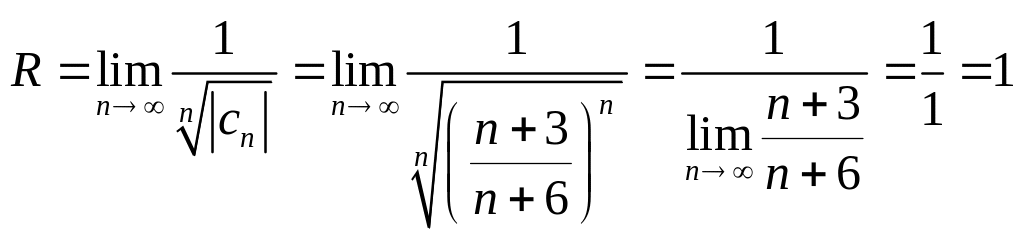Отже, , а повернувшись до старої змінної, матимемо . Розв’язавши нерівність, отримаємо: , .

Тепер перевіримо збіжність ряду на границях інтервалу збіжності:

а) , підставивши в даний ряд, отримаємо

– це знакопочережний ряд, до якого застосуємо ознаку Лейбніца. За другим пунктом цієї ознаки, маємо

,

отже, за ознакою Лейбніца ряд є розбіжним, а це означає, що не належить інтервалу збіжності.

б) , підставивши це значення в даний ряд, матимемо

– останній ряд є розбіжним згідно з пунктом а) досліджень цього прикладу. Тоді значення теж не належить інтервалу збіжності даного ряду.

Отже, ряд є абсолютно збіжним при , у всіх інших точках він є розбіжним.

3. Властивості степеневих рядів

1°. Сума степеневого ряду при всіх значеннях із інтервалу збіжності ряду є неперервною функцією.

2°. Степеневий ряд в його інтервалі збіжності можна почленно диференціювати любу кількість разів і при цьому інтервал збіжності продиференційованих рядів залишається попереднім; так

.

3°. Степеневий ряд можна почленно інтегрувати по любому відрізку, що лежить всередині інтервалу збіжності; ряд отриманий інтегруванням від до має той же інтервал збіжності, що і попередній:

4°. При додаванні збіжних степеневих рядів, які мають загальну область збіжності, отримаємо збіжний степеневий ряд, інтервал збіжності якого дорівнює перетину інтервалів збіжності доданків рядів.