1. Ознаки порівняння

Нехай маємо два додатні ряди: ряд (2), який треба дослідити, та ряд для порівняння:

(5)

Теорема I. Якщо:

а) починаючи з деякого члена, виконується нерівність і ряд (5) є збіжним, то збіжним є і ряд (2);

б) починаючи з деякого члена, виконується умова і ряд (5) є розбіжним, то розбіжним є і ряд (2).

Приклад 5. Дослідити на збіжність ряд .

Розв’язання. Загальний член досліджуваного ряду . Для порівняння виберемо ряд , який є збіжним, оскільки є геометричною прогресією зі знаменником . В той же час між і виконується нерівність (дріб той менший, у якого знаменник більший). Отже, досліджуваний ряд є збіжним.

Теорема II. Якщо існує границя

,

то із збіжності ряду (5), при , прямує збіжність ряду (2), а з розбіжності ряду (2), при , прямує розбіжність ряду (5).

Приклад 6. Дослідити на збіжність ряд .

Розв’язання. Запишемо загальний член заданого ряду . Для порівняння візьмемо гармонічний розбіжний ряд, загальний член якого . Тоді з урахуванням першої важливої границі маємо

.

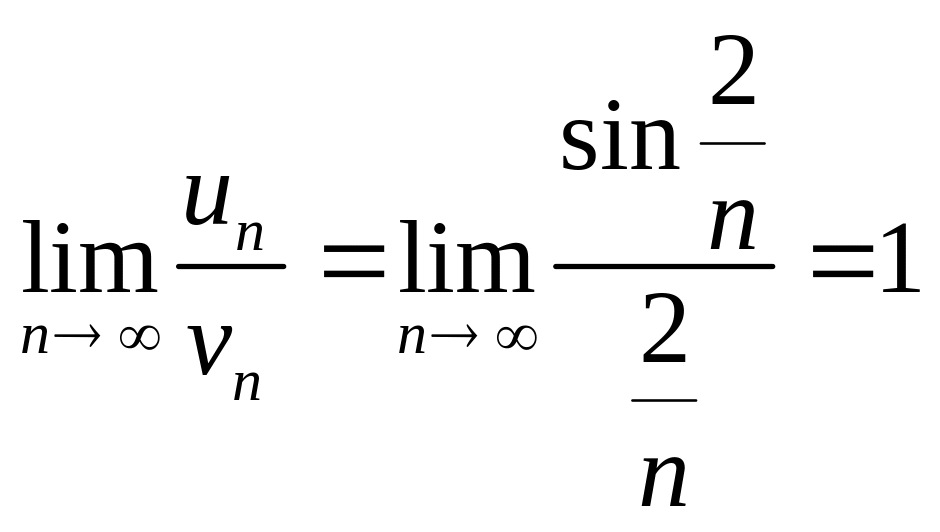Отже, досліджуваний ряд є розбіжним за теоремою II.

Теорема III. Якщо, починаючи з деякого місця (припустимо при ), виконується нерівність

,

то із збіжності ряду (5) прямує збіжність ряду (2), а з розбіжності ряду (2) прямує розбіжність ряду (5).

Приклад 7. Дослідити на збіжність ряд .

Розв’язання. Загальний член даного ряду є . Для порівняння візьмемо ряд, для якого загальний член записується у вигляді . Відомо, що вибраний ряд є нескінченно спадною геометричною прогресією і є збіжним. Застосуємо теорему III. Знайдемо відношення

; .

Порівнявши ці відношення, встановлюємо, що

; .

Отже, даний ряд є збіжним.

При дослідженні рядів за допомогою ознак порівняння необхідно знати, які з рядів (5) є збіжними, а які розбіжними.

Для порівняння часто користуються рядами:

1)

2)

Перший з цих рядів, як відомо, називається геометричною прогресією, а другий – ря- дом Діріхле, або узагальненим гармонічним рядом.

2. Ознака д’Аламбера

Якщо для ряду з додатними членами (2) існує границя , то:

1) ряд збіжний при ;

2) ряд розбіжний при .

Якщо , то питання про збіжність ряду потребує допоміжних досліджень.

Приклад 8. Дослідити на збіжність ряд

Розв’язання. Скористаємося ознакою Д’Аламбера: , .

.

Заданий ряд збіжний.

3. Ознака Коші

Якщо для ряду (2) з додатними членами існує границя то

1) ряд збіжний при ;

2) ряд розбіжний при .

Якщо , то питання про збіжність ряду потребує допоміжних досліджень.

Приклад 9. Дослідити на збіжність ряд .

Розв’язання. Застосуємо ознаку Коші, отримаємо

,

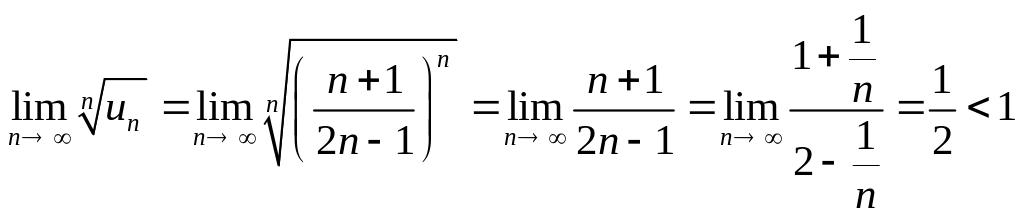тобто даний ряд є збіжним.

4. Інтегральна ознака Коші

Нехай задано ряд

, (6)

члени якого є значеннями неперервної, додатної і монотонно спадної функції на проміжку .

Тоді ряд (6) є збіжний, якщо збіжним є невласний інтеграл , і розбіж-ний, якщо цей інтеграл є розбіжним.

Зауваження. Нижньою границею інтегрування може бути любе друге додатне число з області існування функціїї . Щоб отримати функцію , потрібно в загальному члені ряду замість покласти .

Приклад 10. Дослідити на збіжність ряд .

Розв’язання. За умовою , тоді .

На проміжку ця функція неперервна, додатна і монотонна. Запишемо невлас-ний інтеграл і обчислимо його

.

Невласний інтеграл є розбіжним, отже розбіжним є і заданий ряд.