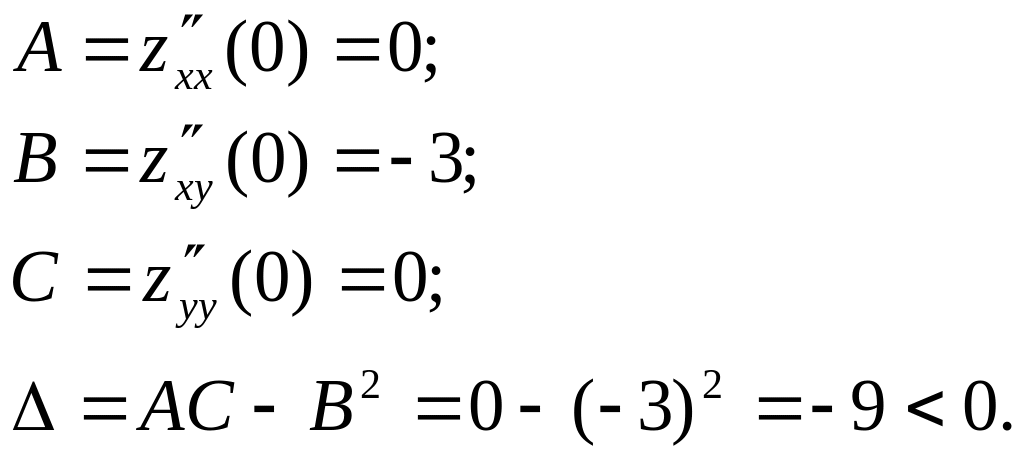7. 9. Локальный экстремум функции

Термины «максимум» и «минимум» функции нескольких переменных имеют тот же смысл, что и для функции одной переменной.

Определение. Точка называется точкой максимума (минимума) функции , если существует окрестность точки такая, что для всех точек из этой окрестности выполняется неравенство

; .

Теорема (необходимое условие экстремума). Если точка есть точка экстремума дифференцируемой функции , то частные производные и в этой точке равны нулю.

Следствие. Если точка соответствует экстремуму функции , то .

Определение. Точки, в которых обе частные производные первого порядка функции обращаются в нуль ( ), называются стационарными точками.

Замечание. Дифференцируемая функция может и не иметь экстремума в стационарной точке.

Теорема (достаточное условие экстремума). Пусть в стационарной точке функция имеет непрерывные частные производные второго порядка

Тогда функция имеет в точке экстремум, если

,

причём,

• если 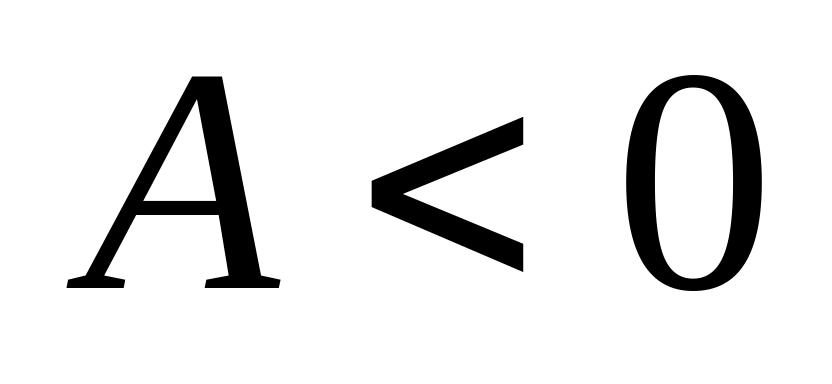— максимум,

• если — минимум.

Если , то функция экстремума не имеет,

если , то теорема ответа на вопрос о наличии экстремумов не даёт.

Пример. Найти экстремум функции . Найдём частные производные и : Решим систему уравнений и найдём стационарные точки функции z Получим две точки и . Найдём частные производные второго порядка и вычислим их значения в каждой из стационарных точек: Проверим достаточное условие экстремума. а) Рассмотрим точку Поэтому в точке функция экстремума не имеет. б) Рассмотрим точку . Таким образом, функция в точке имеет экстремум. Так как , то в точке - минимум.

7.10. Условный экстремум функции

Условный экстремум находится тогда, когда переменные х и у функции , не являются независимыми, т.е. существует некоторое соотношение -(х, у) = 0, связывающее переменные х и у, которое называется уравнением связи.

Так как только одна из переменных х и у может считаться независимой, то другая может быть выражена через первую из уравнения связи. Тогда можно записать, что . В таком случае справедливо соотношение:

.

В точках экстремума должно выполняться условие , т.е.:

.

Кроме того, дифференцируя уравнение связи , нетрудно получить:

.

Умножим последнее равенство на некоторое число  и сложим его с предшествующим соотношением:

После перегруппировки получим:

Таким образом, для отыскания условного экстремума функции необходимо найти значения параметра , которые будут обеспечивать выполнение последнего соотношения.

Для этого необходимо, рассмотреть систему трех уравнений:

и найти удовлетворяющие ей значения величин .

Введем функцию Лагранжа L(x,y,)=f(x, y)+(x, y) и с ее использованием сформулируем следующую теорему.

Теорема (необходимое условие условного экстремума). Пусть в области задана функция с уравнением связи (х, у) = 0, пусть существуют частные производные первого порядка функций z и  во всех точках области D. Тогда, чтобы точка была бы точкой условного экстремума функции z при условии (х, у) = 0 необходимо, чтобы существовало такое , что величины удовлетворяли бы системе уравнений, составленной для функции Лагранжа:

.

Замечание. Последнее условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Использование функции Лагранжа для нахождения точек условного экстремума функции называется методом множителей Лагранжа.

Пример. Найти экстремум функции z= f(x, y) = xy, если уравнение связи имеет вид 2x + 3y – 5 = 0. Составим функцию Лагранжа: . Составим систему необходимых условий для отыскания условного экстремума: 2x + 3y – 5 = 0. То есть: Решая последнюю систему уравнений, получим: Таким образом, функция имеет условный экстремум в точке = .

Теорема (достаточное условие условного экстремума). Пусть в области задана функция z = f( x, y) с уравнением связи (х,у) = 0, пусть существуют непрерывные частные производные второго порядка функции z во всех точках D. Тогда, чтобы точка была бы точкой условного экстремума функции z при условии (х,у) = 0 достаточно чтобы:

.

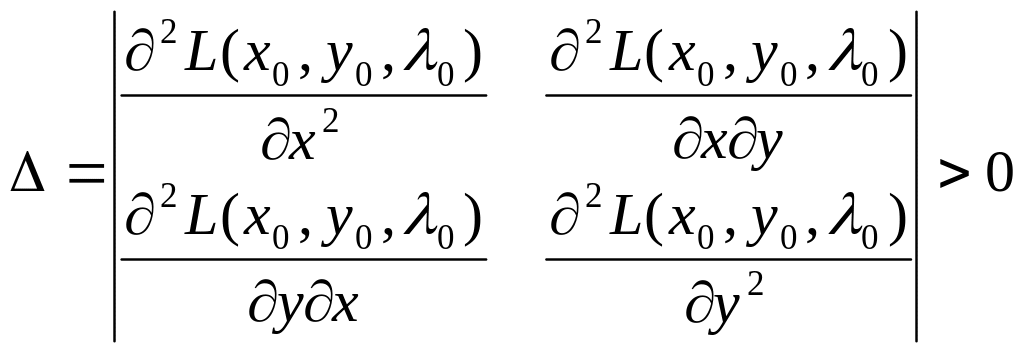При этом:

• если 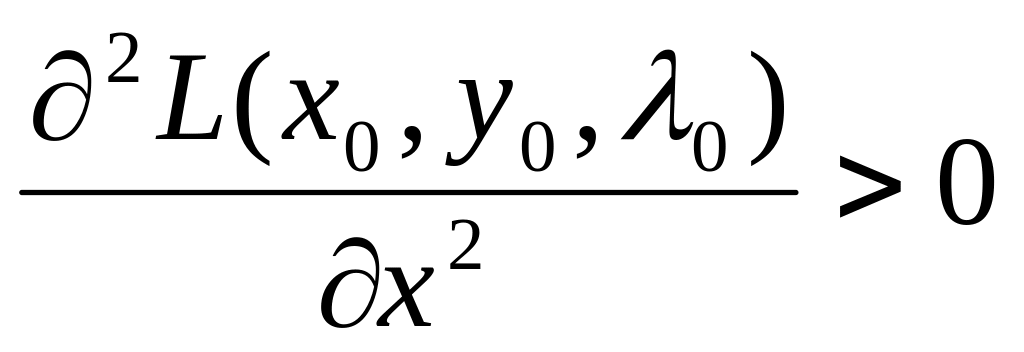, то точка - есть точка условного минимума,

• если , то точка - есть точка условного максимума.

Если , то точка не является точкой условного экстремума,

если , то необходимо дополнительное исследование.