7.7. Градиент

Определение. Пусть в некоторой области D задана функция . Тогда вектор с координатами , называется градиентом функции в точке и обозначается как :

.

Пусть – орт вектора (т.е. единичный вектор , имеющий то же направление , что и вектор ). Тогда выражение для производной по направлению можно записать как скалярное произведение двух векторов и , т.е.:

.

Следовательно:

.

По определению скалярного произведения

где – угол между векторами и .

Так как , то окончательно получаем:

. (*)

Таким образом, связь градиента с производной по направлению определяется следующей теоремой.

Теорема. Пусть задана функция и поле градиентов .

Тогда производная функции по направлению некоторого вектора равна проекции вектора на вектор :

.

Из выражения (*) следует, что производная по направлению в точке будет наибольшей, если это направление совпадает с направлением градиента функции в точке (в этом случае ):

.

Таким образом, градиент дифференцируемой функции в точке определяет направление, в котором функция в этой точке возрастает с наибольшей скоростью. (В физике существуют такие понятия как градиент температуры, градиент давления и т.п., т.е. это направления наиболее быстрого роста функций температуры, давления и др.) При этом модуль градиента:

равен наибольшей скорости изменения функции z в точке .

Из равенства (*) следует также, что если векторы и перпендикулярны, то производная по напрвлению равна нулю. Это значит, что функция в точке в направлении не меняется, т.е. указанное направление будет касательным к линии уровня в точке .

Отсюда следует еще одно свойство градиента: направление вектора совпадает с направлением нормали к линии уровня функции , проходящей через точку .

Пример. Задана функция z= .Найти градиент функции в точке и величину градиента функции в этой точке. Предварительно находим частные производные первого порядка и их значения в заданной точке: Теперь воспользуемся формулами отыскания координат вектора градиента и его величины: , .

7.8. Выпуклость функции

Определение. Множество называется выпуклым, если отрезок, построенный на двух точках принадлежащих этому множеству, содержится в множестве D.

Рис.

Определение. Функция , определенная на множестве , называется выпуклой вверх (вниз) на множестве D, если для любых двух точек и любого выполняются условия:

( ).

Если в последних условиях неравенства строгие, то функция называется строго выпуклой вверх (вниз).

Теорема (необходимое и достаточное условие выпуклости). Пусть функция определена на выпуклом и открытом множестве , пусть существуют ее частные производные второго порядка

,

тогда:

• функция будет выпукла вниз на множестве D, если для любого :

,

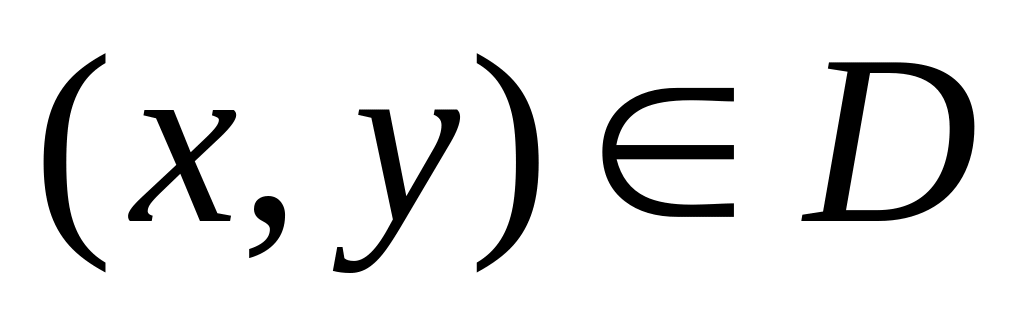• функция будет выпукла вверх на множестве D, если для любого :

.

Теорема (достаточное условие строгой выпуклости). Пусть функция определена на выпуклом и открытом множестве , пусть существуют частные производные второго порядка

,

тогда :

• функция будет строго выпукла вниз на множестве D, если для любого :

,

• функция будет строго выпукла вверх на множестве D, если для любого :

.

Пример. Задана функция . Исследовать функцию на выпуклость в области Вычислим производные, необходимые для проверки условий теоремы: , , , . Таким образом, A и B в исследуемой области имеют различные знаки. Следовательно, функция z не обладает свойством выпуклости.