7.5. Производная сложной функции

Теорема. Пусть задана функция , причем , . Пусть функции и определены в окрестности точки , т.е. и . Пусть существуют конечные производные и . Пусть функция дифференцируема в точке . Тогда существует производная :

.

Пример. Найти производную функции z= f(x,y) по переменной t, если , , . Вычислим производные функции f(x,y) по переменным x и y: , . Вычислим производные функции x(t) и y(t) по переменной t: , . Тогда: .

7.6. Производная по направлению

Рассмотрим функцию , определенную в некоторой области . Пусть – некоторая точка области , – вектор любого направления. Перейдем из точки в некоторую точку в направлении вектора . Функция получит при этом приращение .

Разделим приращение функции на длину отрезка . Полученное отношение дает среднюю скорость изменения функции на участке . Тогда предел этого отношения при (если он существует и конечен) будет являться скоростью изменения функции в точке в направлении вектора .

Определение. Предел называется производной функции в точке по направлению вектора .

Производную функции в точке по направлению вектора обозначают как или .

Помимо величины скорости изменения функции, позволяет определить и характер изменения функции в точке в направлении вектора , т.е.:

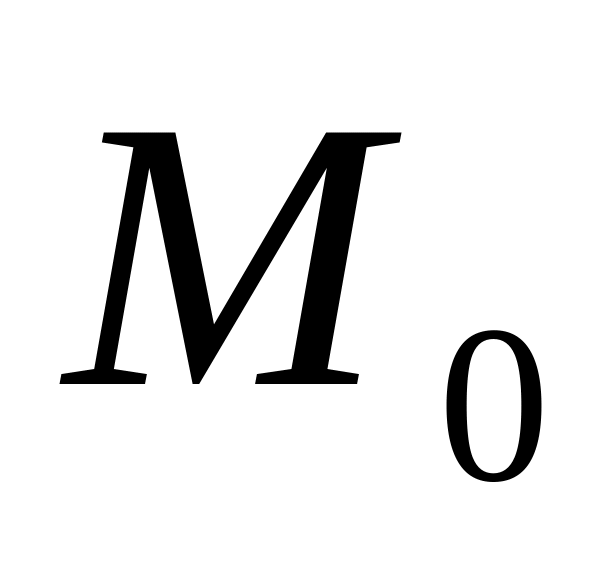• если , то функция в точке в направлении вектора возрастает;

• если 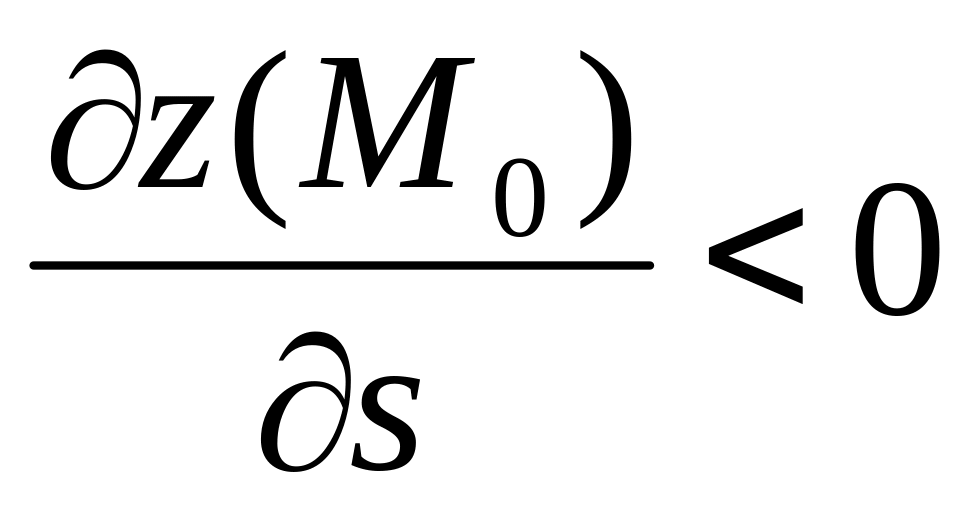, то функция в точке в направлении вектора убывает;

• если , то в направлении вектора функция не изменяется.

Таким образом, направление вектора – есть направление линии уровня функции, проходящей через точку (вектор является касательным к линии уровня в точке ).

Замечание. Частные производные функции являются частным случаем производной по направлению: - это производная функции по направлению вектора , – производная функции по направлению вектора .

Теперь получим выражение для производной функции по направлению . Предположим, что функция дифференцируема в точке . Тогда

,

где — бесконечно малые функции при .

Положим = , тогда:

, ,

где – направляющие косинусы вектора (Рис….).

Рис….

Следовательно:

.

Разделив последнее выражение на и перейдя к пределу при , получим выражение для производной функции по направлению в точке :

=

Пример. Вычислить производную функции z =f(x,y)= x2 + y2x в точке А(1, 2) по направлению вектора , В (3, 0). Определим координаты вектора =(3-1; 0-2) = (2; -2) = 2 . Далее определяем модуль этого вектора: = Найдем частные производные функции z в общем виде: . Вычислим значения этих величин в точке А : . Для нахождения направляющих косинусов вектора произведем следующие преобразования: = За величину принимается произвольный вектор, направленный вдоль заданного вектора, определяющего направление дифференцирования. Из последнего соотношения получаем значения направляющих косинусов вектора : cos = ; cos = - Окончательно получаем: - значение производной функции z по направлению вектора в точке A .