7. Функции нескольких переменных

7.1. Основные понятия

Определение. Если каждому значению переменных из некоторого множества соответствует одно определённое значение переменной величины , то говорят, что задана функция нескольких переменных

Также как и в случае функции одной переменной называются независимыми переменными или аргументами, - зависимой переменной, множество - областью определения функции.

Очевидно, что функция, удовлетворяющая данному определению является однозначной.

Пример. Найти область определения функции двух переменных . Функция принимает действительные значения при переменных , удовлетворяющих системе: , или . Первому неравенству удовлетворяют координаты точек, лежащих внутри и на окружности ; второму неравенству удовлетворяют координаты точек, лежащие внутри параболы ; пересечение этих областей задает область определения функции z (Рис. 21). Рис. 21

Определение. Графиком функции n переменных называется множество точек принадлежащих пространству , таких что:

.

Графиком функции двух переменных является множество точек трёхмерного пространства , образующее некоторую поверхность в .

График функции трёх и более переменных изобразить наглядно уже не возможно. Поэтому для изучения поведения функции многих переменных используют специальные приёмы и понятия. Важнейшими из них являются линии (поверхности) уровня.

Определение. Линией уровня функции двух переменных называется множество точек плоскости, таких, что во всех этих точках значение функции постоянно, т.е. . Число называется уровнем.

Известным примером линий уровня являются параллели и меридианы на глобусе. Это линии уровня функций широты и долготы.

Если рассматривается функция большего чем двух, числа переменных, то говорят уже о поверхностях уровня.

Пример. Для функции построить линии уровня. Рассмотрим , тогда , т.е. линии уровня для данной функции — концентрические окружности.

7.2. Предел и непрерывность

Все свойства пределов и свойства бесконечно малых, которые были сформулированы для функции одной переменной, переносятся на функции нескольких переменных.

Для наглядности изложения будем рассматривать функцию двух переменных , хотя все исказанное останется справедливым и для функции большего числа переменных.

Определение. Число называется пределом функции в точке (при и ), если для любого существует число такое, что для всех точек , отстоящих от точки на расстояние, меньшее, чем , выполняется неравенство

.

Предел функции двух переменных записывается как: .

Пример. Вычислить предел . Перепишем функцию в виде: . Введём новую переменную . Так как при и , то имеем: . Кроме того, , поэтому . Пример. Существует ли ? Пусть точка стремится к точке по прямой , проходящей через точку . Тогда получим: . Таким образом, приближаясь к точке по различным прямым, соответствующим различным значениям , получаем разные значения предела. Отсюда следует, что предел функции в точке не существует.

Определение. Функция называется непрерывной в точке , если

причем точка (x,y) стремится к точке (x₀,y₀) произвольным образом.

Как было указано ранее, важным классом непрерывных функций одной переменной являются функции, непрерывные на отрезках. Они обладают рядом отличительных свойств. Аналогичные свойства имеют место и для непрерывных функций переменных, если их рассматривать в областях некоторого специального вида. Для того чтобы сформулировать эти свойства, необходимо ввести ряд определений.

Определение. Если = и = точки пространства , то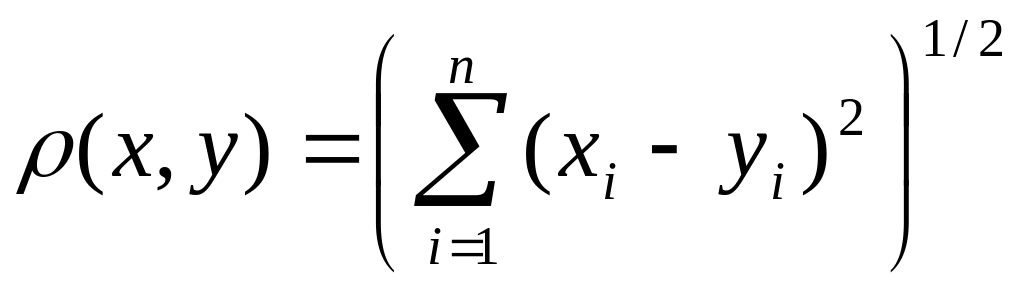 - есть расстояние между этими точками.

Определение. -окрестностью точки называется множество точек , таких что расстояние от этих точек до точки всегда меньше , т.е. .

Определение. Точка называется внутренней точкой множества , если существует -окрестность точки полностью принадлежащая множеству , т.е. .

Определение. Множество всех внутренних точек множества называется внутренностью множества и обозначается .

Определение. Множество, целиком состоящее из внутренних точек, называется открытым.

Определение. Точка называется граничной точкой множества , если для любого существует -окрестность точки , которая содержит точки как принадлежащие множеству так и не принадлежащие ему.

Определение. Множество всех граничных точек множества называется границей множества .

Определение. Открытое множество, содержащее свою границу, называется замкнутым.

Определение. Множество называется связным, если любые две точки этого множества можно соединить непрерывной кривой, состоящей из точек этого множества.

Пример. Множество точек, принадлежащих кругу – связное множество. Множество точек, принадлежащих двум непересекающимся кругам и - не связное множество.

Определение. Связное открытое множество называется областью.

Определение. Связное замкнутое множество называется замкнутой областью.

Определение. Область, целиком лежащая в некоторой -окрестности точки , называется ограниченной.

Базируясь на данных определениях, можно сформулировать теоремы для непрерывных функций двух переменных.

Теорема. Если функция z=f(x, y) определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется по крайней мере одна точка (x₁, y₁), такая, что для остальных точек области верно неравенство

f(x₁, y₁)  f(x, y)

а также точка (x₂, y₂), такая, что для всех остальных точек верно неравенство

f(x₂, y₂)  f(x, y)

тогда f(x₁, y₁) = M – наибольшее значение функции, а f(x₂, y₂) = m – наименьшее значение функции f(x, y) в области D.

Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере одного наибольшего и одного наименьшего значения.

Теорема. Если функция z=f(x, y) определена и непрерывна в замкнутой ограниченной области D, а M и m – соответственно наибольшее и наименьшее значения функции в этой области, то для любой точки c [m, M] существует точка N₀(x₀, y₀) такая, что f(x₀, y₀) = c.

Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция f(x, y) по крайней мере один раз обращается в ноль.

Теорема. Функция z=f(x, y), непрерывная в замкнутой ограниченной области D, ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство .

Аналогичную формулировку имеют теоремы для функций большего, чем двух, числа переменных.