2.2 Метод Ейлера
Однокрокові методи призначені для розв’язування диференціальних рівнянь першого порядку виду
(1.1)
Метод Ейлера є найпростішим методом розв’язування задачі Коші. Він дозволяє інтегрувати ДР першого порядку. Точність його не велика.
Тобто крива заміняється дотичними. Рух відбувається не по інтегральній кривій, а по відрізках дотичної .
Метод
Ейлера базується на розкладі функції
в ряд Тейлора в околі точки
(1.2)
Якщо
мале, то, члени розкладу, що містять в
собі
і т.д. є малими високих порядків і ними
можна знехтувати.
Тоді
(1.3)
Похідну
знаходимо з рівняння (1.1), підставивши
в нього початкову умову. Таким чином
можна знайти наближене значення залежної
змінної при малому зміщенні
від початкової точки. Цей процес можна
продовжувати, використовуючи
співвідношення.
,
роблячи як завгодно багато кроків.
Похибка
методу має порядок
,
оскільки відкинуті члени, що містять
в другій і вище степенях.
Недолік методу Ейлера - нагромадження похибок, а також збільшення об’ємів обчислень при виборі малого кроку з метою забезпечення заданої точності.
В
методі Ейлера на всьому інтервалі h
тангенс кута нахилу дотичної приймається
незмінним і рівним
.
Очевидно, що це призводить до похибки,
оскільки кути нахилу дотичної в точках
та
різні. Точність методу можна суттєво
підвищити, якщо покращити апроксимацію
похідної.
Це можна зробити, якщо, наприклад, використати середнє значення похідної на початку та в кінці інтервалу. В т.з. модифікованому методі Ейлера (метод Ейлера з перерахунком) спочатку обчислюється значення функції в наступній точці за звичайним методом Ейлера.
(1.4)
Воно
використовується для обчислення
наближеного значення похідної в кінці
інтервалу
.
Обчисливши
середнє між цим значенням похідної та
її значенням на початку інтервалу,
знайдемо більш точне значення
:
(1.5)
Принцип модифікованого методу можна пояснити інакше. Якщо в розкладі в ряд Тейлора зберегти член з
(1.6)
Замість
другої похідної
можна використати наближення кінцевою
різницею
(1.7)
.
Підставивши (1.7) в (1.6) одержимо
(1.8)
Що
співпадає по формі з (5). Відмінність між
( 1.8) та (1.5): в (1.5) точне значення похідної
замінимо на
.
Похибка при такій заміні має порядок
.
Відмітимо, що за підвищення точності доводиться платити додатковими затратами машинного часу.
В обчислювальній практиці використовується також метод Ейлера-Коші з ітераціями:
знаходиться грубе початкове наближення (за звичайним методом Ейлера)
будується ітераційний процес
(1.9)
Ітерації
продовжують до тих пір, доки два послідовні
наближення не співпадуть з заданою
похибкою
.
Якщо після декількох ітерацій співпадання
нема, то потрібно зменшити крок
.
Тобто в модифікованому методі Ейлера, в методі Ейлера-Коші з ітераціями спочатку (на першому етапі) знаходиться наближення для , а потім воно вже коригується за формулами (5) або (9).
РОЗДІЛ 3
3.1 Постановка задачі.
Дослідимо систему Чуа розв’язавши систему лінійних диференціальних рівнянь методом Ейлера.
3.2 Вибір способу реалізації.
Було обрано спосіб реалізації в об’єктно орієнтованому середовищі Qt на операційній системі Linux Ubuntu 12.04 . При реалізації використовується метод Ейлера для розв’язання системи лінійних диференціальних рівнянь.
3.3 Результат.
Було проведено декілька дослідів, перший з константами за яких виконується ланцюг Чуа, інші три зі зміненими константами для того щоб виявити як поводить себе система при змінах різних початкових даних.
1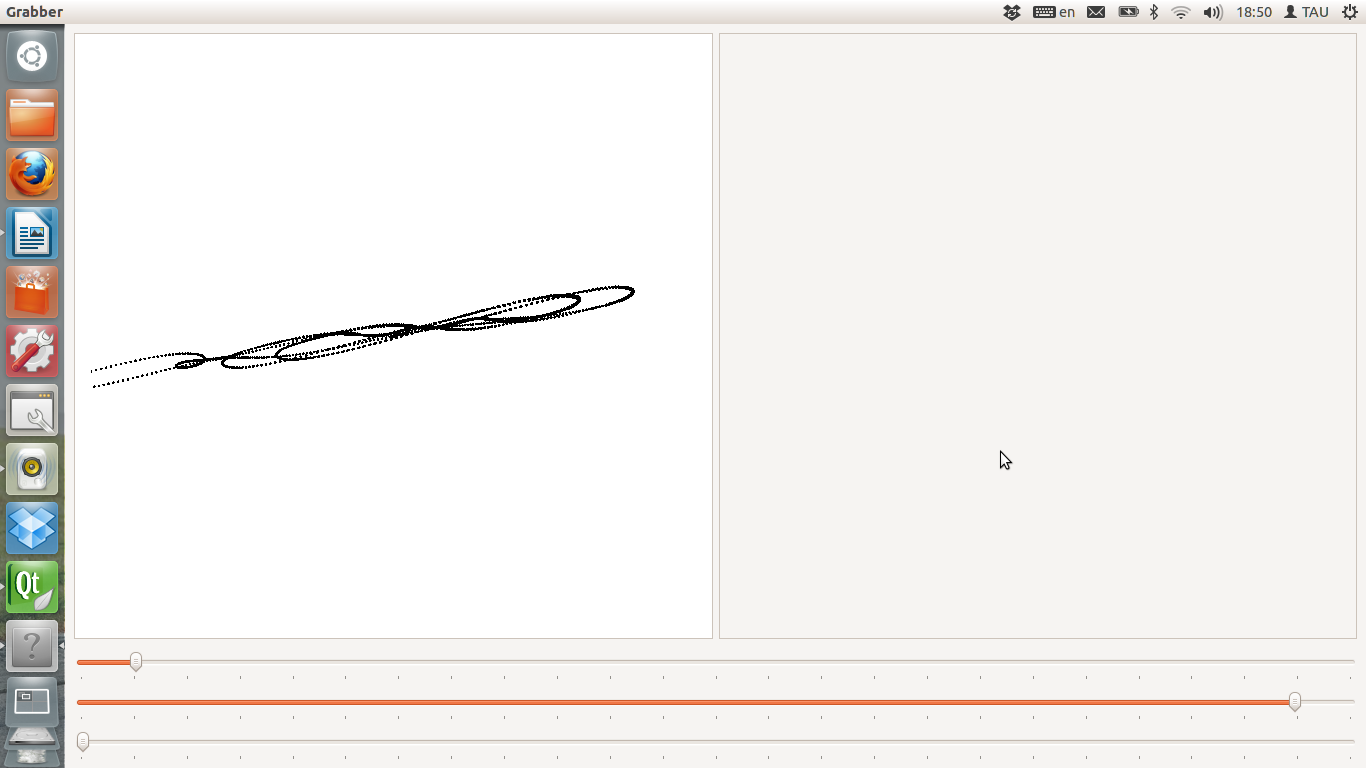
.
float c1=1/9;
float c2=1.0f;
float l=1/7;
float ga=-0.8f;
float gb=-0.5f;
float g=0.7f;
float alpha=9;//c2/c1;
float beta=1*7/(0.7*0.7)
На рисунках показані часові залежності коливань, що виявляються даною системою.
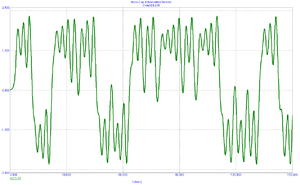
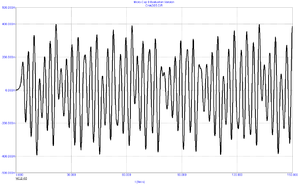
У випадку 2, 3, 4 були змінені деякі константи для того щоб дослідити як змінюється поведінка системи та до яких констант найбільш чутлива.
2. Була змінена константа ga з -0,8 на -0,7
f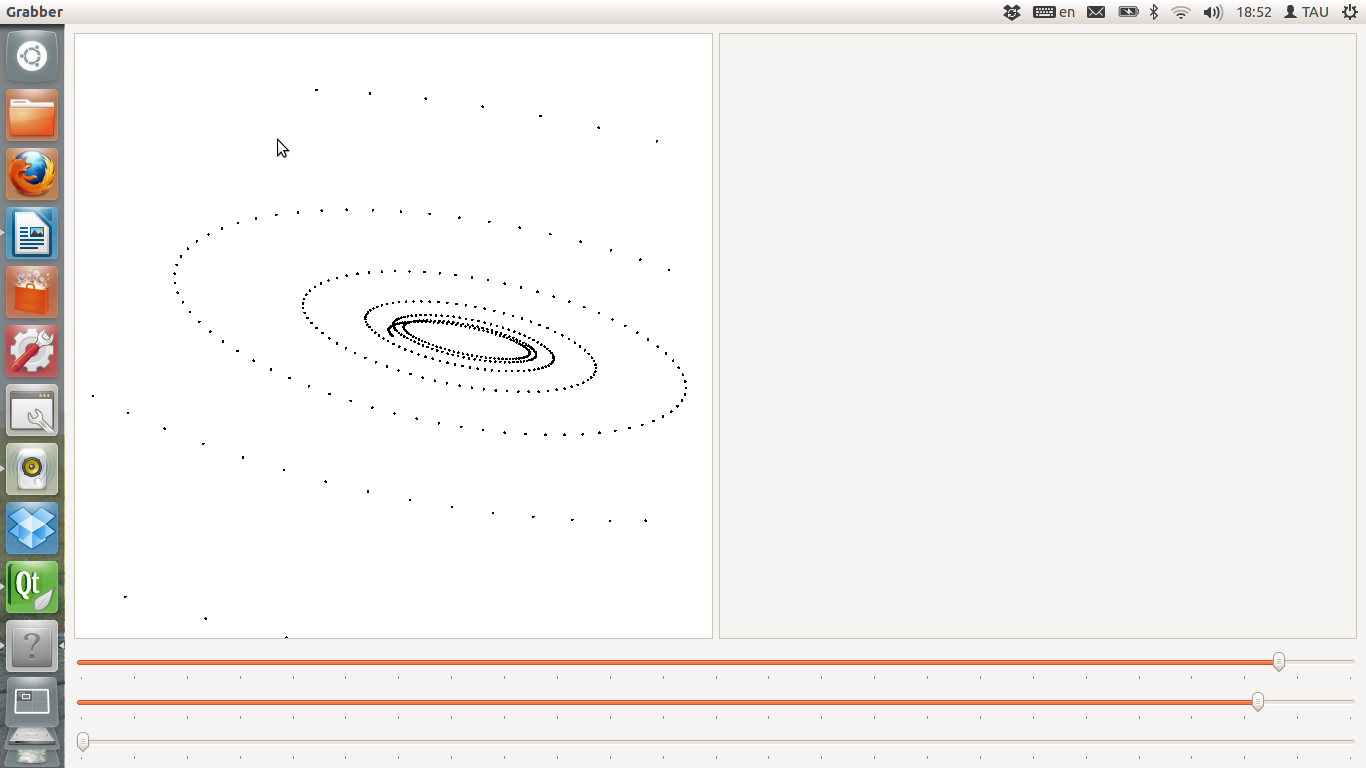
loat
c1=1/9;
float c2=1.0f;
float l=1/7;
float ga=-0.7f;
float gb=-0.5f;
float g=0.7f;
float alpha=9;//c2/c1;
float beta=1*7/(0.7*0.7);
3 .Стала ga була відновлена до початкової і змінена c2 з 1 на 1,2
float c1=1/9;
float c2=1.2f;
float l=1/7;
float ga=-0.8f;
float gb=-0.5f;
float g=0.7f;
float alpha=9;//c2/c1;
float beta=1*7/(0.7*0.7);
4.
float c1=1/9;
float c2=1.0f;
float l=1/7;
float ga=-0.8f;
float gb=-0.4f;
float g=0.7f;
float alpha=9;//c2/c1;
float beta=1*7/(0.7*0.7);