§ 11. Энтропия
Так как теплоемкость в общем случае изменяется от нуля до бесконечности, определение теплоты по уравнению (2.17) возможно не для любых процессов (например, при сx = ±∞). Кроме того, теплоемкость не является параметром состояния и не дает возможности представить теплоту процесса графически. Следовательно, для общего выражения теплоты процесса необходим еще один параметр состояния.
31
Для вывода этого параметра рассмотрим уравнение (2.26). Поскольку δq не является полным дифференциалом, правая часть этого уравнения du + pdv также не является полным дифференциалом. Выражения такого типа в высшей математике называют дифференциальными двучленами (так как du и dv - полные дифференциалы). В соответствии с одной из теорем высшей математики дифференциальный двучлен можно превратить в полный дифференциал некоторой новой функции, если разделить его на интегрирующий делитель. Допустив, что интегрирующим делителем для δq является абсолютная температура Т (справедливость этого допущения будет доказана в § 27) и, обозначив новую функцию символом s, получим
Эта функция была введена в конце XIX в. Р. Клаузиусом и названа энтропией. Поскольку ds является полным дифференциалом, энтропия является функцией (параметром) состояния, ее изменение в процессе не зависит от его пути и определяется значениями в начальном и конечном состоянии. Изменение энтропии в цикле равно нулю:
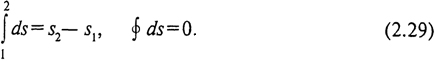
Энтропия обладает свойством аддитивности, согласно которому sm = S, S = ∑ Sj. Удельная энтропия s измеряется в Дж/(кг∙К). За начало отсчета энтропии может быть принято любое состояние вещества.
Энтропия относится к числу калорических параметров состояния и может быть представлена в зависимости от любой пары термических параметров s = (v, T); s = φ(p, T)\ s = ψ(p, v).
В соответствии с (2.28) теплоту любого обратимого процесса можно выразить через изменение энтропии
Так как абсолютная температура всегда положительна, знаки теплоты и изменения энтропии в обратимых процессах всегда одинаковы. Подвод теплоты к рабочему телу (δq > 0) сопровожается увеличением энтропии (ds > 0), отвод теплоты (δq < 0) - уменьшением энтропии (ds < 0).
§ 12. Тепловая диаграмма
С введением энтропии общее число термических и калорических параметров состояния возросло до шести: р, v, Т, u, i, s. Все они однозначно связаны между собой термическим уравнением состояния, калорическими уравнениями состояния для внутренней энергии и для энтальпии, уравнениями связи энтропии с термическими параметрами, поэтому в качестве независимых переменных в общем случае может быть выбрана любая пара из этих параметров. Часто в качестве независимых параметров используются Т и s. Если в диаграмме Т - s нанести линию какого-либо процесса T = φ(s) (рис. 3, а), то в соответствии с геометрической интерпретацией определенного интеграла (2.30) площадь 1d22'1' определит теплоту этого процесса. Диаграмму T - s называют тепловой. С ее помощью легко доказать, что теплота является функцией процесса. Если между точками 1 и 2 осуществить процесс по пути 1b2, то площадь под линией процесса будет больше.
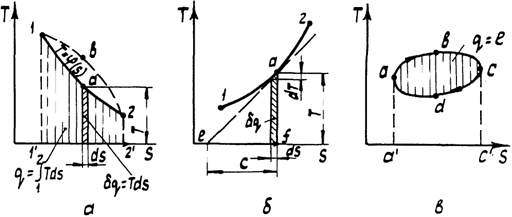Рис.
3. Тепловая диаграмма: а - определение
теплоты процесса; б - определение
теплоемкости; в - определение работы
цикла
Примечательным свойством тепловой диаграммы является возможность графического определения истинной теплоемкости в любой точке процесса. Для этого в заданной точке (рис. 3, б) необходимо провести касательную к линии процесса. Истинная теплоемкость в точке а определится отрезком подкасательной с на оси s. Доказательство следует из подобия двух прямоугольных треугольников с вершинами в точке а: элементарного (с катетами dT и ds) и aef (c катетами Т и с). Равенство отношений катетов dT/ds = Т/с с учетом (2.30) приводит к полученному ранее уравнению (2.16) для истинной теплоемкости
Площадь замкнутой фигуры цикла в диаграмме Т - s, как и в диаграмме p - v, определяет работу цикла (рис. 3, в). На участке abc цикла энтропия увеличивается, следовательно, теплота, эквивалентная площади abcc'a', подводится к рабочему телу. На участке cda теплота, эквивалентная площади adcc'd, отводится от рабочего тела. Суммарная теплота цикла определится площадью его замкнутой фигуры abcd. Поскольку для цикла ∮ du = 0, из уравнения первого закона термодинамики (2.26) следует, что q = l = пл. abcd.
33