§ 9. Определение теплоты процесса. Теплоемкость

Теплообмен системы с окружающей средой в общем случае сопровождается изменением температуры, поэтому количество теплоты в каком-либо процессе часто выражают через изменение температуры тел в этой системе.

Количество теплоты, которое нужно подвести (или отвести) в данном процессе для изменения температуры тела на 1 К, называют теплоемкостью. В технической термодинамике удобнее всего использовать понятие удельной теплоемкости: массовой с_x, отнесенной к 1 кг вещества и измеряемой в Дж/(кг∙К); молярной μс_x, отнесенной к 1 молю вещества и измеряемой в Дж/(моль∙К); объемной с'_x, отнесенной к 1 м³ вещества при нормальных физических условиях и измеряемой в Дж/(м³∙К). Связь между указанными удельными теплоемкостями определяется соотношением

где μ - молярная масса, кг/моль; v₀ - удельный объем при нормальных физических условиях, м³/кг.

(В дальнейшем будем пользоваться преимущественно понятием массовой теплоемкости).

Теплоемкость является функцией процесса, т. к. для изменения температуры тела на 1 К в различных процессах требуется разное количество теплоты. Числовое значение теплоемкости в различных процессах может изменяться от - ∞ до = + ∞. Индекс х в обозначении теплоемкости в каждом конкретном случае указывает на условия протекания процесса. Например, теплоемкость процесса постоянного давления обозначается c_p теплоемкость процесса постоянного объема - c_v. Теплоемкости этих двух процессов наиболее изучены и чаще всего используются в расчетах.

Теплоемкости реальных процессов изменяются в зависимости от параметров процесса. Чаще всего эту зависимость выражают в переменных p и Т: c_x = f(p, T). Теплоемкость в данной точке процесса называют истинной теплоемкостью и определяют по изменению температуры в элементарном процессе

Следовательно, теплота процесса является его функцией и может быть выражена через истинную теплоемкость этого процесса

Истинные теплоемкости реальных газов с_p; c_v; μc_p; μc_v; c'_p; c'_v определяются экспериментально; их значения приводятся в специальных таблицах.

Для интегрирования уравнения (2.17) необходимо знать, как изменяется в данном процессе теплоемкость с_x в зависимости от температуры. Эту зависимость иногда трудно выразить аналитически, поэтому на практике для определения теплоты пользуются понятием средней теплоемкости процесса с_xm в заданном интервале изменения температуры

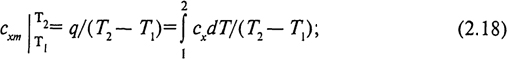
Если известна средняя теплоемкость процесса, то

Значение средних теплоемкостей с_pm; c_vm; (μc_p)_m; (μc_v)_m; c'_pm; c'_vm; для реальных газов также определяются экспериментально и приводятся в специальных таблицах для интервала температур от 0 °С до t°C - с_xm|

t

0

. Тогда теплоту процесса можно выразить через табличные значения средних теплоемкостей

§ 10. Аналитические выражения первого закона термодинамики

Для возможности исследования различных термодинамических систем уравнение первого закона в общем виде (2.4) необходимо преобразовать с учетом термодинамической классификации видов энергии и определения работы процесса. Такое преобразование осуществляют в двух вариантах: для открытой и закрытой термодинамических систем.

В условиях открытой термодинамической системы (см. рис. 1, б) при установившемся движении потока изменение его энергии будет складываться в общем случае из изменения внутренней энергии, внешней потенциальной энергии давления, внешней потенциальной энергии положения и кинетической энергии. Для единичного массового расхода

Под внешней работой понимается техническая работа

В результате подстановки (2.21) и (2.22) в уравнение (2.4) с использованием соотношений (1.8) и (2.13) получим развернутое уравнение первого закона термодинамики, справедливое для обратимых и необратимых процессов:

30

Сумма первых двух слагаемых в правой части уравнения (2.23) представляет собой изменение энтальпии: du + d(pv) = d(u + pv) = di, сумма остальных трех слагаемых в соответствии с (2.14) - располагаемую работу δl₀. Поэтому уравнение первого закона термодинамики для открытой системы можно представить в более простой форме:

Таким образом, теплота, подведенная к потоку, в общем случае расходуется на изменение его энтальпии и на располагаемую работу.

Для обратимых процессов δl₀ = - vdp, поэтому

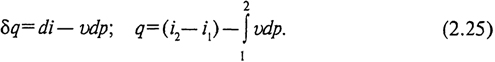
Это уравнение является наиболее удобным при анализе процессов в открытых системах.

Для закрытых систем (рис. 1, а) уравнение первого закона термодинамики удобнее представить через изменение внутренней энергии. Если в (2.23) три последних слагаемых представить как располагаемую работу, то для обратимых процессов можно записать

Поскольку d(pv) = pdv + vdp, окончательно получим

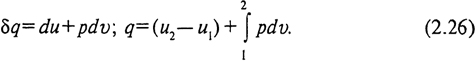
Второе слагаемое в (2.26) представляет собой работу изменения объема. Следовательно, в общем случае теплота, подведенная к системе, расходуется на изменение внутренней энергии и на работу изменения объема: