§ 8. Определение работы процесса
Механическое взаимодействие термодинамической системы с окружающей средой в общем случае осуществляется в формах работы перемещения и работы изменения объема. Всякая элементарная механическая работа может быть определена как произведение обобщенной силы Р на приращение обобщенной координаты dx:
Например, в случае перемещения в гравитационном поле обобщенной силой является вес тела Р = mg, где g = 9,8 м/с2 - ускорение свободного падения, а обобщенной координатой - расстояние h от центра масс до выбранного нуля отсчета. Элементарная работа перемещения в гравитационном поле δL = mgdh.
В современных тепловых машинах и холодильных установках имеет место преимущественно работа изменения объема рабочих тел. Для определения работы изменения объема, например за счет подвода теплоты извне, рассмотрим простейшую термодинамическую систему - объем 1 кг газа в цилиндре под поршнем (см. рис. 1, а). В результате подвода теплоты δq газ нагреется, и его объем увеличится на dv. Поршень при этом переместится на расстояние dh, совершая работу δl против силы сопротивления окружающей среды, которая равна произведению внешнего давления р' на площадь поршня. Следовательно, элементарная работа изменения объема определится как δl = p'fdh. Так как fdh = dv, окончательно получим:
В тех случаях, когда объем системы не изменяется (dv = 0) или отсутствует внешнее сопротивление (p' = 0), работа изменения объема равна нулю (δl = 0). При наличии внешнего сопротивления (р' > 0) работа расширения положительна (dv > 0, δl > 0), а работа сжатия отрицательна (dv < 0, δl < 0).
Для обратимых процессов, являющихся равновесными (р' = р), работа изменения объема может быть определена с помощью только внутренних параметров системы
При изменении объема в конечном процессе от v1 до v2
Для интегрирования уравнения (2.8) необходимо знать, как изменяется давление в зависимости от удельного объема в данном процессе, т. е. р = φ (v). Если эта функция задана графически в диаграмме р - v (рис. 2, а), то работа изменения объема может быть представлена площадью 122'1', ограниченной линией процесса и осью v, поэтому диаграмма р - v называется рабочей.
В термодинамическом процессе в условиях открытой системы (см. рис. 1, б) работа совершается (затрачивается) не только благодаря изменению объема вещества, но и в результате механического перемещения потока. При изменении удельного объема в системе от v1 до v2 позади идущий поток на участке х1 выполняет работу наполнения р1f1х1 = p1v1, а на участке х2 затрачивается работа выталкивания (преодоления сопротивления) впереди идущего потока р1f2х2 = p2v2. Таким образом, располагаемая работа потока l0 складывается из работы наполнения, работы изменения объема и работы выталкивания. Элементарная располагаемая работа
Вычитаемое в уравнении (2.9) представляет собой элементарное изменение энергии давления. Учитывая, что d(pv) = pdv + vdp, окончательно получим
Анализ уравнения (2.10) показывает, что в обратимом процессе положительная располагаемая работа (δl0 > 0) может быть получена лишь при понижении давления в потоке (dp < 0). Для повышения давления в потоке (dp > 0) необходимо затрачивать работу извне (δl0 < 0). Если давление в потоке не изменяется (dp = 0), то располагаемая работа равна нулю (δl = 0).
При изменении давления в конечном процессе от p1 до p2
Для интегрирования этого уравнения необходимо знать зависимость p = φ(v) в данном процессе. Располагаемая работа в диаграмме p - v (см.рис. 2, а) представлена площадью 122''1'', ограниченной линией процесса и осью р.
Следует отметить, что понятие располагаемой работы справедливо и для закрытой системы. Например, при подъеме поршня в результате расширения газа в цилиндре часть работы расширения будет затрачиваться на вытеснение окружающей среды из пространства
над поршнем. В результате располагаемая работа газа будет также определяться по уравнениям (2.10) и (2.11).
Для цикла ∮ d(pv) = 0, поэтому как следует из уравнения (2.9), δl0 = δl; l0 = l. Работа цикла графически изображается площадью его замкнутой фигуры (см. рис. 2, б). В цикле abcd на участке abc совершается работа расширения, эквивалентная площади abcc'a', a на участке cda затрачивается работа сжатия, эквивалентная площади adcc'a'. Алгебраическая сумма этих работ и определяет работу цикла, эквивалентную площади abcd.
С помощью диаграммы р - v (см. рис. 2, в) легко доказать, что работа является функцией процесса. В зависимости от пути процесса из состояния 1 в состояние 2 площадь под линией процесса (работа расширения) различна (lla2 > llb2).
Уравнения (2.7), (2.8), (2.10), (2.11) и их графическая интерпретация в диаграмме p - v справедливы для обратимых процессов. В необратимых процессах часть работы затрачивается на преодоление трения и полностью идет на пополнение запаса тепловой энергии (lтр = qтр). Работа (теплота) трения определяется экспериментально. Располагаемая работа в необратимых процессах:
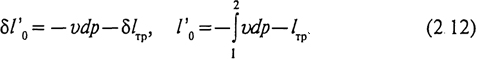
Аналогичным образом может быть определена и работа изменения объема в необратимых процессах.
Сопоставление уравнений (2.10), (2.11) и (2.12) показывает, что необратимость приводит к уменьшению совершаемой (положительной) работы и к увеличению затраченной извне (отрицательной) работы. Работа обратимого расширения оказывается максимальной, а работа обратимого сжатия - минимальной.
В тепловых машинах и установках за счет располагаемой работы L0 осуществляется изменение внешней кинетической энергии потока ΔЕк = т(с22-c12 )/2 изменение внешней потенциальной энергии положения ΔEп = mg (h2 - h1) и совершается техническая (полезная) работа Lтех (см. рис. 1, б). В зависимости от назначения установки под технической работой можно понимать, например, вращение ротора турбины или коленчатого вала двигателя, отвод электроэнергии во внешнюю сеть в МГД-генераторе при движении плазмы в магнитном поле и т. д. Во всех этих случаях техническая работа положительна (ΔLтех > 0). Техническая работа может подводиться к потоку извне (ΔLтех < 0), например, для привода компрессора или насоса. Таким образом, L0 = т(с22-c12 )/2 + mg(h2 - h1) + Lтех. В элементарном процессе для единичной массы вещества
следовательно
