§ 6. Внутренняя энергия. Энтальпия

Внутренняя энергия U обладает свойством аддитивности, согласно которому внутренняя энергия сложной системы равна сумме внутренних энергий входящих в нее частей: U = ∑ U_j, где j = 1, 2... - порядковые номера частей системы. Измеряется U в Дж.

Внутренняя энергия u = U/m, отнесенная к единице массы вещества, называется удельной внутренней энергией и измеряется в Дж/кг. В дальнейшем для краткости величину u будем называть просто внутренней энергией. Внутренняя энергия относится к числу калорических параметров состояния, поэтому du является полным дифференциалом. В соответствии с этим изменение внутренней энергии в процессе целиком определяется ее значениями в начальном (и₁) и конечном (и₂) состоянии и не зависит от пути процесса. Изменение внутренней энергии в цикле равно нулю:

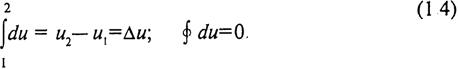
Для практических расчетов за начало отсчета внутренней энергии может быть принято любое состояние вещества.

Внутренняя энергия может быть выражена как функция любой пары основных термических параметров. Зависимости такого рода называются калорическими уравнениями состояния. Наиболее употребительным является калорическое уравнение в переменных v и Т:

В соответствии с современными представлениями о микроструктуре вещества внутренняя энергия тела складывается из внутренней кинетической энергии u_к, внутренней потенциальной энергии и_п и нулевой энергии u₀:

Внутренняя кинетическая энергия определяется поступательным и вращательным движением молекул и колебательным движением атомов в молекуле. Она является функцией абсолютной температуры, u_к = f(T). Внутренняя потенциальная энергия определяется силами взаимодействия между молекулами. Величина этих сил зависит от расстояния между молекулами, т. е. от удельного объема вещества. Следовательно, u_п = f(v). Сумму внутренней кинетической и потенциальной энергии часто называют тепловой энергией. Именно в этом смысле понятие тепловой энергии широко используется в технической и справочной литературе. Нулевая энергия определяется силами внутримолекулярного, внутриатомного и внутриядерного взаимодействия. В процессах, не связанных с химическими и ядерными превращениями, нулевая энергия остается постоянной, а изменяется только тепловая часть внутренней энергии.

Непрерывность действия тепловых машин, аппаратов и установок чаще всего обеспечивается при использовании потоков рабочих тел, что соответствует принципу открытой термодинамической системы. Такая система (см. рис. 1, б) обменивается с окружающей средой не только теплотой и работой, но и веществом. Изменение состояния массы вещества в выбранных границах открытой системы происходит одновременно с перемещением этой массы в результате упругого взаимодействия со смежными массами внешнего потока на границах системы. Каждая единичная масса вещества, движущегося в канале, стремится вытолкнуть впереди идущую единичную массу за счет потенциальной энергии давления, полученной потоком в начале пути (от насоса, компрессора и т. п.). Следовательно, изменение состояния и перемещение массы вещества в открытой системе органически связано с перемещением смежных масс внешнего потока, движущихся впереди и позади системы. Поэтому, в отличие от внешнего взаимодействия системы с окружающей средой в форме работы и теплоты, упругое взаимодействие с внешним потоком является для системы внутренним процессом, в связи с чем открытую систему называют еще расширенной термодинамической системой.

При неразрывном установившемся движении потока массовый расход вещества G (в кг/с) в любом сечении системы и на ее границах одинаков и может быть определен по уравнению неразрывности (или сплошности):

где f - сечение канала, м², с - скорость потока, м/с.

Потенциальная энергия давления Е_д, полученная потоком в начале пути, переносится потоком и затрачивается на его перемещение по каналу. Для единичной массы вещества (G = 1 кг/с) эта энергия е_д может быть определена как работа проталкивания через рассматриваемое сечение и выражена как произведение силы на перемещение. Например, для сечения f₁ (рис. 1, б) на входе в систему при перемещении х₁, е = р₁х₁ = р₁v₁ где р₁f₁ - сила, a f₁x₁ = v₁ - удельный объем. Для произвольного сечения канала

Следовательно, энергия давления определяется параметрами состояния потока и составляет неотъемлемую часть его энергии, поэтому для потока вещества определяющим параметром будет уже не внутренняя энергия, а сумма удельной внутренней энергии и энергии давления, называемая энтальпией i. Удельная энтальпия (в Дж/кг)

Энтальпия обладает свойством аддитивности. Для произвольной массы вещества I = mi = U + pV; I = ∑ I_j. В соответствии с уравнением (1.9) энтальпия является параметром состояния, поскольку представляет собой комбинацию величин - параметров состояния. Элементарное изменение энтальпии di является полным дифференциалом, а изменение энтальпии в процессе не зависит от пути процесса и определяется ее значениями в начальном и конечном состоянии. Изменение энтальпии в круговом процессе равно нулю.

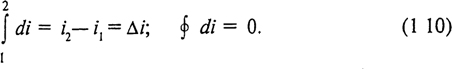
За начало отсчета энтальпии может быть принято любое состояние вещества. Энтальпия относится к числу калорических параметров состояния и может быть представлена как функция любой пары термических параметров. Наиболее употребительным является калорическое уравнение в переменных р и Т: