Параметры режима несимметричного к.З в точке к.З.

Согласно методу симметричных составляющих, расчет несимметричных к.з. проводят по правилу эквивалентности тока прямой последовательности, в соответствии с которым ток прямой последовательности любого несимметрично к.з. может быть определен как ток при трехфазном коротком замыкании в точке, удаленной от действительной точки к.з. на дополнительное сопротивление z_Δ, зависящее от вида несимметрии [3, c. 328].

Рассчитываем составляющие токов и напряжений в месте двухфазного к.з. на землю.

Граничные условия: , ,

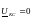
Ток прямой последовательности:

,

где - шунт двухфазного короткого замыкания на землю [1, c.18]:

Модуль периодической слагаемой тока поврежденной фазы при K^(1,1) можно определить по выражению:

где - коэффициент, характеризующий вид к.з. [1, c.18].

Симметричные составляющие токов по месту КЗ:

Определяем фазные токи в точке K^(1,1) через симметричные составляющие:

Где – оператор фазы.

Определяем фазные значения симметричных составляющих векторов напряжения в точке K^(1,1). Для особой фазы при двухфазном КЗ на землю:

Фазные напряжения через симметричные составляющие:

- остаточное напряжение неповрежденной фазы;

Требуемые величины рассчитаны, граничные условия выполняются.

Для рассмотренной несимметрии построим векторные диаграммы напряжений (рис. 2.12) и токов (рис. 2.13).

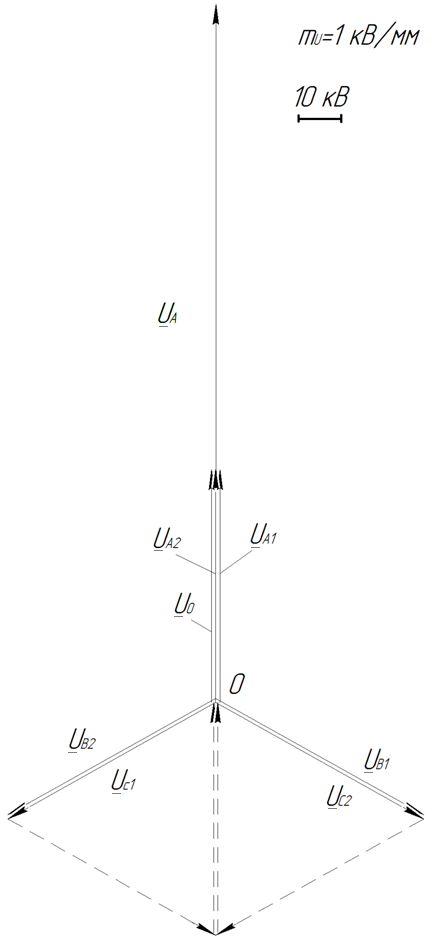
Рисунок 2.12 Векторная диаграмма напряжений

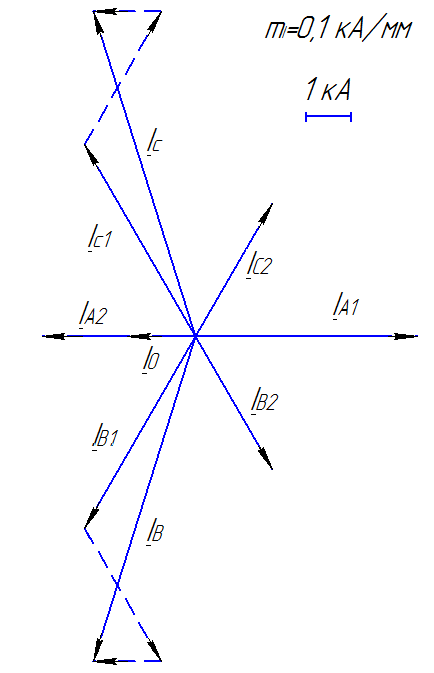
Рисунок 2.13 Векторная диаграмма токов

Режим 2. Между цепями Л1 отсутствует взаимная индуктивность; реактор в нейтрали ТР3 установлен; режиму соответствует .

Определить сопротивление реактора в нейтрали ТР3, исходя из условий: (замечание: должно быть приведено к ступени 230 кВ).

Влияние взаимной индуктивности и наличие реактора в нейтрали трансформатора оказывают влияние только на величину сопротивления нулевой последовательности. Поскольку известно, что в обоих режимах модули периодической составляющей тока неповрежденной фазы равны и определяются по выражению:

то из равенства модулей тока следует равенство величин сопротивления нулевой последовательности:

Параметры схемы замещения для второго режима возьмем из расчета первого режима за исключением реактивностей линии, а также в схему замещения войдет утроенное сопротивление реактора, включенного в нейтраль трансформатора ТР3.

Реактивности нулевой последовательности первого и второго участков второй цепи при отсутствии взаимной индуктивности между цепями:

- где - сопротивления прямой последовательности первого и второго участка второй цепи, на которой имеет место несимметрия;

- коэффициент, учитывающий взаимную индукцию между фазами одной цепи и влияние троса [1, табл.6].

Реактивность первой цепи:

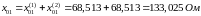
_{Схема замещения, соответствующая 2му режиму поперечной несимметрии, представлена на рисунке 2.14.}

Рисунок 2.14 Схема замещения нулевой последовательности

для второго режима

Преобразуем сопротивления из «треугольника» в звезду:

Сопротивления обмоток трансформатора с расщепленной обмоткой ТР3 преобразуем в сопротивление (рис. 2.15):

Рисунок 2.15 Преобразование схемы замещения нулевой последовательности

Сопротивления преобразуем в сопротивление , а - в сопротивление :

Рисунок 2.16 Преобразование схемы замещения нулевой последовательности

Тогда для сопротивления нулевой последовательности можно записать выражение:

Сделав необходимы преобразования, получим выражение для сопротивления реактора :
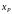