5. Натуральные величины отрезков прямых линий и углов наклона прямых линий к плоскостям проекций.

Д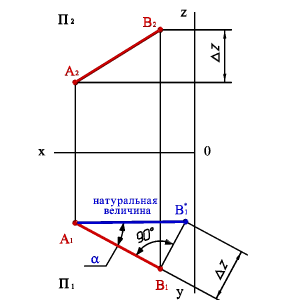 лину отрезка АВ и - угол наклона отрезка к плоскости П₁ можно определить из прямоугольного треугольника АВС |AС|=|A₁B₁|, |BС|=DZ. Для этого на эпюре (рис.31) из точки B₁ под углом 90⁰ проводим отрезок |B₁B₁*|=DZ, полученный в результате построений отрезок A₁B₁* и будет натуральной величиной отрезка АВ, а угол B₁A₁B₁*= . Рассмотренный метод называется методом прямоугольного треугольника.

6. Взаимное положение прямых линий.

1. Прямые могут быть пересекаться между собой и тогда точки пересечения их одноименных проекций лежат на одной линии связи (рисунок а).

2. Прямые могут скрещиваться между собой и тогда точки пересечения их одноименных проекций не лежат на одной линии связи (рисунок б).

3. Прямые могут быть параллельны между собой и тогда их одноименные проекции также параллельны между собой (рисунок в).

а)              б)                                  в)

Теорема. Если одна сторона прямого угла параллельна плоскости проекций (или лежит в ней), то прямой угол проецируется на эту плоскость без искажения.

7. Задание плоскости общего и частного положения на чертеже. Положение плоскости относительно плоскостей проекций.

В отличие от линии, плоскость на комплексном чертеже не может быть задана своими проекциями. Плоскость считается беспредельной, неограниченной, а поэтому проекции её точек на P₁ и P₂ займут всё поле чертежа.

• Три точки (АВС), не лежащие на одной прямой;

• Прямая (а) и точка (А), ей не принадлежащая;

• Две пересекающиеся прямые (а и б);

• Две параллельные прямые (а||б).

Плоскость относительно плоскостей проекций может занимать как общее, так и частное положение.

Плоскость общего положения — плоскость не перпендикулярная ни к одной из плоскостей проекций. Рассмотрим пример комплексного чертежа плоскости общего положения, заданной тремя точками, не лежащими на одной прямой: А, В, С, т. е. треугольник АВС (рис. 2.18). Спроецируем точки А, В, С на все три плоскости проекций, и получим ортогональные проекции плоскости, заданной треугольником АВС. Каждая проекция плоскости АВС, есть треугольник.

Плоскость частного положения — плоскость, которой принадлежат проецирующие прямые, т.е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Именно поэтому ее иногда называют проецирующей плоскостью.

На рисунке представлена горизонтально-проецирующая плоскость, т.е. перпендикулярная к П₁. И поэтому она проецируется на П₁ в виде прямой линии.

На рисунке представлена фронтально-проецирующая плоскость, т.е. перпендикулярная к П₂. И поэтому она проецируется на П₂ в виде прямой линии.

На рисунке представлена профильно-проецирующая плоскость, т.е. перпендикулярная к П₃. И поэтому она проецируется на П₃ в виде прямой линии.

Если плоскость перпендикулярна сразу к двум плоскостям проекций, то она называется плоскостью уровня. Следовательно, плоскость уровня всегда параллельна одной из плоскостей проекций. Существует три вида плоскостей уровня

1. Горизонтальная плоскость уровня — параллельная П₁

2. Фронтальная плоскость уровня — параллельная П₂

3. Профильная плоскость уровня — параллельная П₃