1. Предмет и метод инженерной графики

Инженерная графика - это наука создания проекционных изображений, которая состоит из двух частей: начертательной геометрии и технического черчения.

Начертательная геометрия — раздел геометрии, в котором пространственные формы с их геометрическими закономерностями изучаются в виде их изображений на плоскости.

Начертательная геометрия ставит перед собой 2 задачи:

1. Прямая ― научиться изображать на плоскости по оригиналу трехмерные геометрические объекты.

2. Обратная ― по заданному чертежу восстановить положение оригинала в пространстве.

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записи геометрических предложений и решения задач в начертательной геометрии предлагается использовать геометрический язык, составленный из следующих обозначений и символов.

1. Геометрическая фигура обозначается − Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

A, B, C, D, …,L, M, N, …

1, 2, 3, 4, …, 12, 13, 14, …

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

a, b, c, d, …,l, m, n, …

Линии уровня обозначаются: h − горизонталь; f − фронталь; p − профильная прямая;

Для прямых используются также следующие обозначения:

(AB) − прямая, проходящая через точки A и B;

[AB) − луч с началом в точке А;

[AB] − отрезок прямой, ограниченный точками A и B.

4. Поверхности обозначаются строчными буквами греческого

алфавита:

α, β, γ, δ, …, ζ, η, λ, …

5. Углы обозначаются:

АВС − угол с вершиной в точке В, а также αº, βº, …, φº, ..,

6. Угловая величина (градусная мера) обозначается знаком, который ставится над углом:

φº − величина угла φ.

Прямой угол отмечается квадратом с точкой внутри.

7. Для плоскостей проекций приняты обозначения: π₁ π₂ π₃,

Где π₁ − горизонтальная плоскость проекций;

π₂ − фронтальная плоскость проекций;

π₃ − профильная плоскость проекций;

При замене плоскостей проекций или введении новых плоскостей проекций последние обозначаются π₄, π₅ и т.д.

8. Оси проекций обозначаются: x,y,z, где x − ось абсцисс; y− ось ординат; z − ось аппликат.

Существуют центральный и параллельный методы проецирования.

2. Центральное и параллельное проецирование.

Проекция любой геометрической фигуры есть множество проекций всех ее точек. Направление проецирующих прямых ℓ и положение плоскостей π₁ определяют аппарат проецирования.

Метод центрального проецирования

Е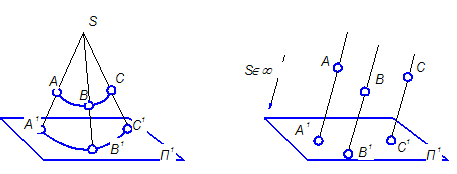 сли дана некоторая плоскость П¹, которую мы назовем плоскостью проекций, центр проекций S вне ее, а также точку А, то проведя через т. А из центра S проецирующий луч, мы получим проекцию т. А на пл. проекций П¹. Если таких произвольно расположенных точек будет несколько, то в итоге мы получим некую коническую поверхность, поэтому этот метод называется еще и коническим. При таком способе проецирования нет размерного соответствия между изображением и моделью. (Рисунок 1)

Метод параллельного проецирования.

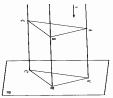
Если точку S удалить от плоскости П' в бесконечность, проеци­рующие лучи будут практически параллельны между собой. Тогда они пересекутся с плоскостью проекций П' в точках А', В', С', кото­рые называются параллельными проекциями точек А, В, С. Соединив, как и в предшествующем случае, точки А', В', С' между собой, полу­чают треугольник А'В'С', который будет уже параллельной проекци­ей треугольника ABC. На рис. 2.3 стрелкой s обозначено направление проецирования.

Если направление s перпендикулярно к плоскости П', то проекция треугольника называется прямоугольной, или ортогональной.

Если направление луча s не перпендикулярно к плоскости П', то проекция треугольника называется косоугольной.