30. Общие понятия о качестве регулирования.

Качество работы системы регулирования в самом общем виде оценивается величиной ошибки, которая равна разности между требуемым и действительным значением регулируемых величин.

Качество САР оценивается по некоторым ее свойствам, определяют которые с помощью критериев качества:

1. Критерии точности - используют величину ошибки в различных типовых режимах.

2. Критерии величины запаса устойчивости – характеризует склонность системы к развитию колебаний.

3. Критерии быстродействия - оценивают быстроту реагирования САР на появление задающего и возмущающего воздействий, определяю длительность переходного процесса.

4. Интегральные (комплексные) критерии - оценивают обобщенные свойства САР: точность, запас устойчивости, быстродействие.

31. Классы динамических звеньев.

32. Принцип управления по возмущению. Область применения. Примеры.

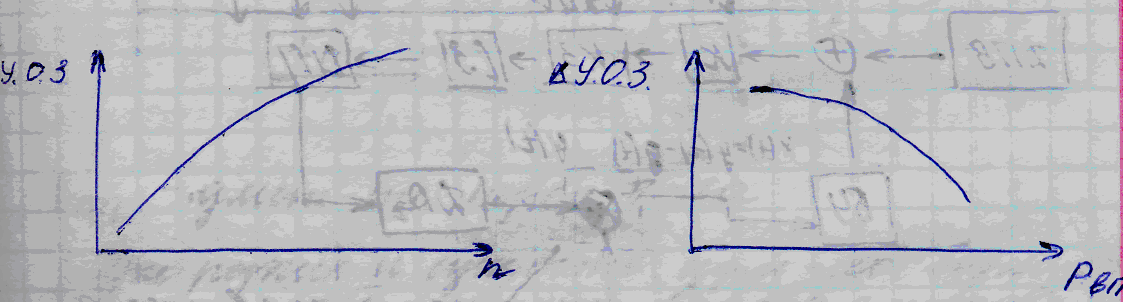
Принцип управления по возмущениям, или принцип компенсации предполагает построение алгоритма работы системы без знания действительного значения регулируемой величины, но с учетом программы регулирования и нескольких наиболее существенных возмущений

ДПВ – датчик поворота вала, φ_КВ – угол пкв, Рвп – давление на впуске (за дросселем), ДЧВ – датчик частоты вращения, БУ – блок управления, ДРвп – датчик давления.

Этот принцип управления применяется, когда требования к качеству регулирования не выполняются разомкнутой системой, когда возмущения, которые нужно учитывать, поддаются измерению.

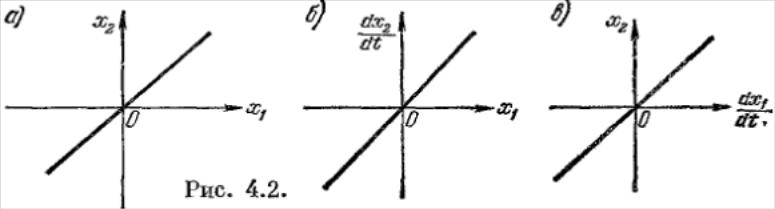
33. Понятие о линейных и нелинейных системах управления. Линеаризация. Оценка устойчивости и качества реальной системы по ее линеаризованной модели.

По виду уравнений или статических характеристик все звенья и все системы в целом делятся на линейные и нелинейные. Если система содержит хотя бы одно нелинейное звено, в целом она будет нелинейной. Анализ нелинейных систем весьма сложен и в большинстве случаем сводится к имитационным или экспериментальным методам, что требует больших затрат машинного времени, изготовления экспериментальных установок и т.д. Теория линейных систем АР разработана довольно полно и дает простые и быстрые методы оценки устойчивости и качества переходных процессов. Поэтому в обязательном порядке производятся попытки преобразовать нелинейную (реальную) систему в линейную путем линеаризации уравнений каждого звена. Нужно выбрать на статической характеристике точку вблизи которой нас интересует поведение звена. Разложить уравнение звена в ряд Тейлора в окрестности точки А.

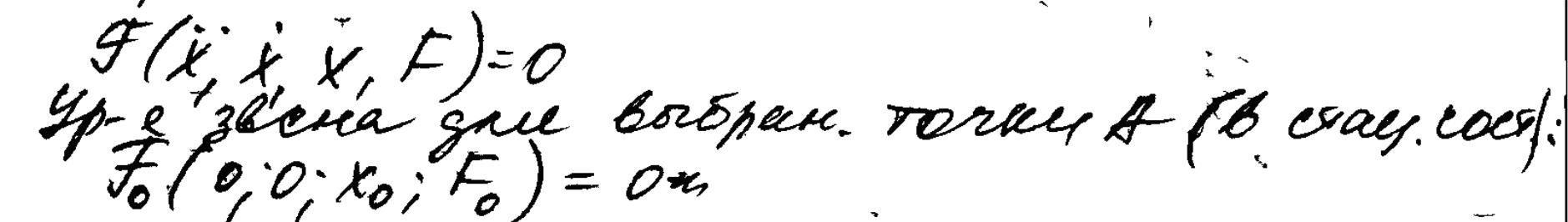
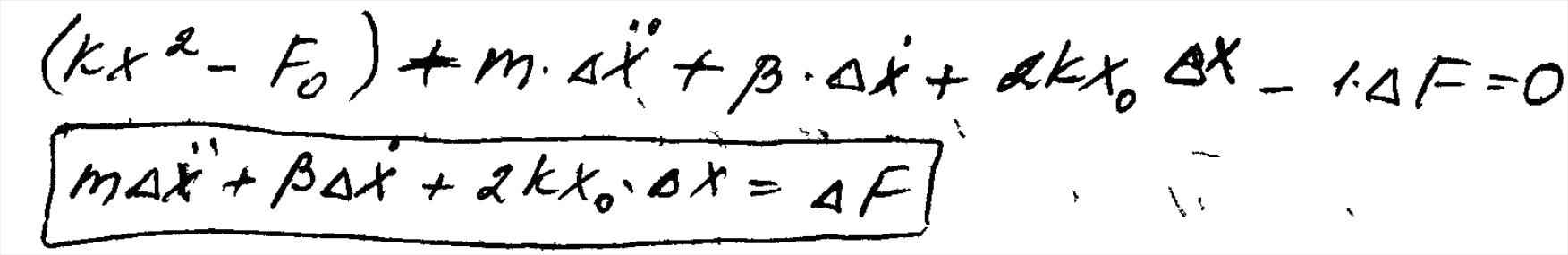
Получим линейное дифференциальное уравнение 2 порядка, которое справедливо в окрестности точки А.

По мере отклонения звена от выбранной точки нарастает погрешность. Поэтому линейное уравнение является приближенным и при значительных отклонениях от выбранной точки необходимо выбирать уравнение положения равновесия и получать другие линейные уравнения. Источник погрешности – отброшенные члены ряда Тейлора.

Нелинейные системы управления.

1. Практически все реальные системы являются нелинейными

2. Поэтьому при анализе любой системы управления, разработчики после составления уравнения звена, пытаются выполнить процесс линеаризации.

3. Выбираем точки А1, А2…Аi в которых нас интересует поведение звена. В этих точках мы проводим касательные и считаем их за статических характеристики звена (линейные).

4. В природе и технике существует множество устройств, для которых невозможна линеаризация – они называются существенно нелинейные.

Типы нелинейности:

1. нелинейность статического типа (нелинейные, кусочно-линейные)

В точке излома рассмотренный метод линеаризации не действует

2. Динамические нелинейности

Динамические нелинейности проявляются только в движении звена при и

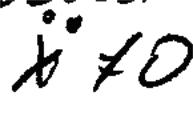
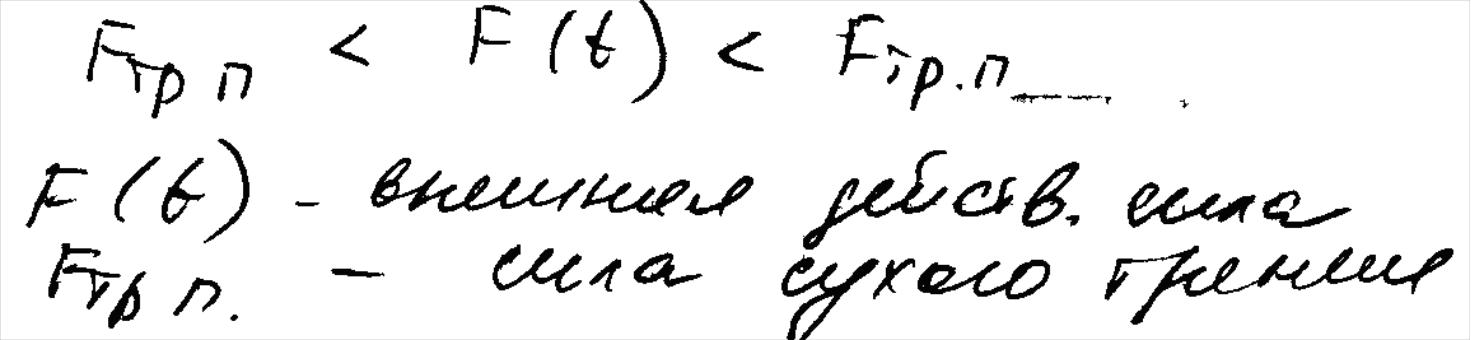
Если в момент времени, при котором скорость тела=0 сумма всех сил, действующих на тело окажется меньше силы сухого трения, то звено остановится.

34. Общие методы повышения точности САР.

35. Переходные функции типовых звеньев.

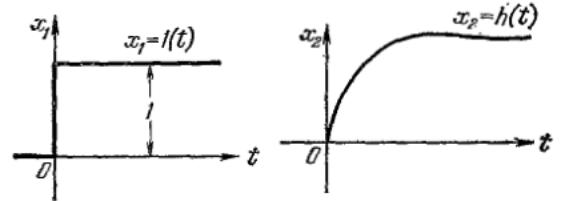
36. Функции веса типовых звеньев.

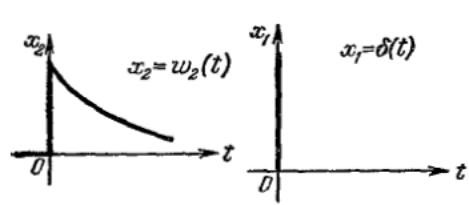
36. Функции веса типовых звеньев.

Весовая функция звена. "Весовой функцией звена к (I) называется оригинал (т. е. обратное преобразование Лапласа) передаточной функции, а именно:

Где — все полюса передаточной функции . Иногда вместо применяют обозначение . В этой фор­муле обозначает вычеты (см. теорию функций комплекс­ного переменного).

П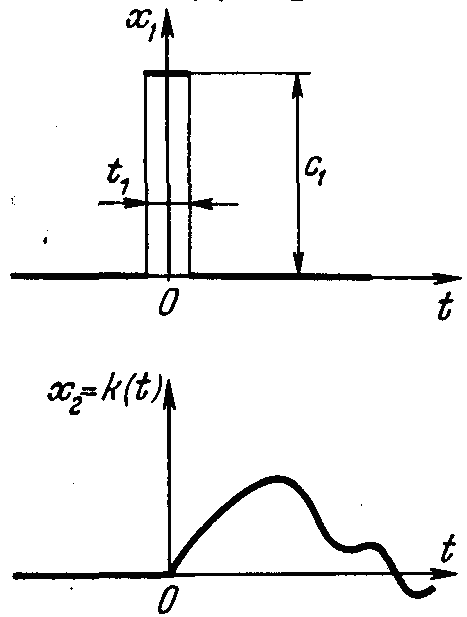 оскольку при нулевых на­чальных условиях согласно (1.6)

то в случае, если , т. е. если — дельта-функ­ция, будет иметь место ра­венство

Известно, что функция представляет собой единичный мгновенный импульс (рис. 1.5),

для которого ,причем площадь .

Следовательно, физический смысл весовой функции звена есть реакция звена на единичный мгновенный импульс, поданный на вход звена.

Иначе говоря, весовая функция представляет собой переходный процесс на выходе звена (рис. 1.5) при подаче на его вход единичного импульса. Поэтому весовую функцию часто называют импульсной переход­ной функцией.

Зная весовую функцию звена , можно определить его передаточную функцию: