1. Процесс составления дифференциального уравнения звена. Линеаризация. Стандартные виды записи уравнения.

Для анализа поведения системы АР необходимо и мат описание, α составляется на базе диф уравнений звеньев системы.

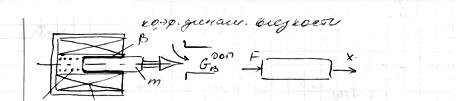
1. Конструктивная схема звена 2) Условное обозн. блоксхема звена

Входным воздействием является сила F, развиваемая эл-маг, выходной координатой является перемещение x неподвижной части.

1. Нужно найти закон, которому подчиняется поведение данного звена mx”=∑Fi

2. Нахождение составляющих данного звена F- сила действующая, со стороны электромагнитного привода; Fтр –трения; Fпр – сила пружины; mx” – сила инерции; mg – сила тяги.

3. Определение математических уравнений для этих составляющих F(t)-внешняя сила; Fтр=βx’ Fпр=cx

4. mx”+ cx+ βx’= F(t) получим дифференциальное уравнение 2-ого порядка, которое точно описывает перемещение золотника под действием внешней силы F.

5. С=kx k-деформация пружины

mx”+ kx²+ βx’

6. Построение статической характеристики звена. Статической характеристикой звена называется зависимость его выходной координаты от входной для ряда установившихся состояний.

Статическая характеристика является нелинейной, что является следствием переменной жесткости пружины.

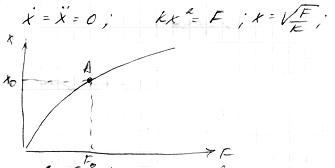
7. Линеаризация уравнения звена. По виду уравнений или стат. хар-к все звенья и все системы в целом делятся на линер. и нелинер. Если система содержит хотя бы одно нелинер. звено в целом оно будет нелинер-ой. Теория нелинер. звена на сегодня не завершена. Анализ весьма сложен и в больш. случаев сводится к иметац. или эксперимент. моделям. что требует больших затрат маш. времени, изготовление экспер. устьановок и тд.

7.1) нужно выбрать на стат харак-ке точку вблизи которой вас интересует поведение звена.

7.2) разложение уравнения звена в ряд тейлора в окрестности точки А. Э(x” x’ x F)=0 mΔx” +βΔx’+2kx₀Δx=ΔF (Лин. диф уравнение 2-ого порядка котрое справедливо в окр-ти точки А)

По мере отклонения корд. от выбранной точки нарастает погрешность. Поэтому лин уравнение явл приближенныйм

8. Приведение уравнения звена к стандартному виду.

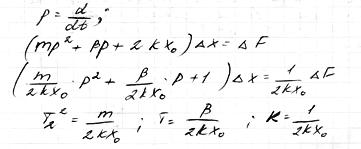
2. Принцип разомкнутого управления. Область применения. Примеры.

При размкнутом ур-е алгоритм работы системы построен без учета возмущений действующих на систему, без знания действующего значения регулируемой величины, а лишь с учетом необходимой программы регилирования.

φ_z регулируемая величина

φ_z = 12⁺³ программа регулирования const (требуется постоянная величина φ_z)

φ_z = 12⁺³ эталонное значение регулируемой величины

Возмущение является любой ф-р (любой физ. природы), к-й вызывает отклонение регулируемой величины от эталонного значения.

Первое основное возмущение это изменение частоты вращения вала двигателя, потому что от него зависит время, отводимое на процесс сгорания.

Второе возмущение – изменение нагрузки на двигатель (измен. расхода воздуха за цикл, или изменение наполнения двигателя) этот фактор изменят скорость горения раб смеси.

К возмущением так же относится изменение тех. состояния двигателя (износ привода системы зажигания, изменение температуры охлажд жидкости)

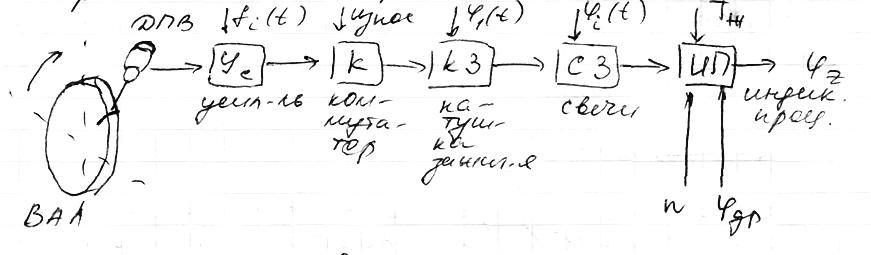
n – частота вращения вала

φ_др - угол открытия дросселя

f(t) – возмущения

Область применения этого принципа в том случае, если требования к качеству регулирования объекта невысокие, если возмущение на объект не вызывает существенного улучшения его показателей и если система достаточно хорошо противостоит этим возмущениям.

u_t - скорость турб. возгорания смеси в рабочей камере.