47. Нейросети- самоообучающиеся адаптивные алгоритмы.

Нейросети(далее НС) работают на основе генетических алгоритмов. Генетические алгоритмы- простая модель эволюции в природе только реализуется в виде комп. программы. В этом алгоритме используются аналоги механизмов генетического наследования и естественного отбора. Нсприменяются практически во всех областях человеческой деятельности, а также на всех уровнях управления предприятий и организаций. Наибольший эффект применения НС достигается там, где есть трудноформализуемая информация и ее большое количество или сложная многомерная зашемленность или искаженность данных, т.е. там ,где невозможно или очень сложно построить математическую модель в у словиях ограниченности времени. Нейрон- элемент или клетка головного мозга, аккумулирующий электр. импульсы, поступающие к нему со стороны входов (дендрит) и передающий аккумулируемый импульс к следующему элементу по передающему волокну или каналу(аксон). Дендриты контактируют с аксонами через специальные образования-синапсы, которые влияют на силу импульса.

Математическая модель биологического процесса:

Х₁w₁

Х₂w₂ I=f(x)

Х₃w₃ аксон

дендриты

х1,х2,…,хn –импульсы(информация); ω1,ω2, …,ωn –веса(синапсы), I-сила входного импульса.

Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. На рис. представлена модель, реализующая эту идею. Хотя сетевые парадигмы весьма разнообразны, в основе почти всех их лежит эта конфигурация.

48.Типы архитектур нейросетей

Из точек на плоскости и соединений между ними можно построить множество графических фигур, называемых графами. Если каждую точку представить себе как один нейрон, а соединения между точками – как дендриты и синапсы, то мы получим нейронную сеть. По архитектуре связей нейросети могут быть сгруппированы в два класса: сети прямого распространения, в которых связи не имеют петель , и сети рекуррентного типа, в которых возможны обратные связи. Сети прямого распространения подразделяются на однослойные перцепротроны (сети) и многослойные перцептроны (сети).Многослойные сети отличаются тем, что между входными и выходными данными располагаются несколько так называемых скрытых слоев нейронов, добавляющих больше нелинейных связей в модель.

Устройство простейшей многослойной нейросети: Любая нейронная сеть состоит из входного слоя и выходного слоя. Соответственно подаются независимые и зависимые переменные. Входные данные преобразуются нейронами сети и сравниваются с выходом. Если отклонение больше заданного, то специальным образом изменяются веса связей нейронов между собой и пороговые значения нейронов. Снова происходит процесс вычислений выходного значения и его сравнение с эталоном. Если отклонения меньше заданной погрешности, то процесс обучения прекращается.

Помимо входного и выходного слоев в многослойной сети существуют так называемые скрытые слои. Они представляют собой нейроны, которые не имеют непосредственных входов исходных данных, а связаны только с выходами входного слоя и с входом выходного слоя. Таким образом, скрытые слои дополнительно преобразуют информацию и добавляют нелинейности в модели.

Среди рекуррентных сетей можно выделить сети Хопфилда и сети Кохонена. С помощью сетей Хопфилда можно обрабатывать неупорядоченные (рукописные буквы), упорядоченные во времени (временные ряды) или пространстве (графики) образцы.Нейросеть Хопфилда можно использовать в качестве ассоциативной памяти. Сеть Кохонена еще называют "самоорганизующейся картой признаков". Сеть такого типа рассчитана на самостоятельное обучение во время обучения сообщать ей правильные ответы необязательно. В процессе обучения на вход сети подаются различные образцы. Сеть улавливает особенности их структуры и разделяет образцы на кластеры, а уже обученная сеть относит каждый вновь поступающий пример к одному из кластеров, руководствуясь некоторым критерием "близости".

Обучение ИНС. Сеть обучается, чтобы для некоторого множества входов давать желаемое множество выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор.Различают алгоритмы обучения с учителем и без учителя. Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой. Обычно сеть обучается на некотором числе таких обучающих пар. Предъявляется выходной вектор, вычисляется выход сети и сравнивается с соответствующим целевым вектором, разность (ошибка) с помощью обратной связи подается в сеть, и веса изменяются в соответствии с алгоритмом, стремящимся минимизировать ошибку. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.Обучение без учителя: Обучающий алгоритм подстраивает веса нейросети так, чтобы получались согласованные выходные векторы, т. е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью.

Общий алгоритм прогнозирования с помощью НС:получение временного ряда с интервалом в выбранную временную итерацию;заполнение «пробелов» в истории;глаживание ряда методом скользящих средних (или другим);получение ряда относительного изменения прогнозируемой величины;формирование таблицы «окон» с глубиной погружения временных интервалов;добавление к таблице дополнительных данных (например, изменение величины за предыдущие годы); шкалирование;определение обучающей и валидационной выборок;подбор параметров нейросети; обучение нейросети;проверка работоспособности нейросети в реальных условиях.

49. ЭТАПЫ ФОРМИРОВАНИЯ КОМПЛЕКСНЫХ ПРОГНОЗОВ. ПРЕДСТАВЛЕНИЯ ВАРИАНТОВ К-Х ПРОГНОЗОВ С ПОМОЩЬЮ ГРАФОВ. ОЦЕНКА СОГЛАСОВАННОСТИ ЧАСТНЫХ ПРОГНОЗОВ И ИСКЛЮЧЕНИЕ ПРОТИВОРЕЧИВЫХ ЧАСТНЫХ ПРОГНОЗОВ(НА ПРИМЕРЕ ГРАФА R=4)

Этапы форм-я:

1. устанавливается степень согласованности м/у данными различных частных методов

W_пр=

2. форм-е новых несогласованных вариантов и разработка граф-варианта

0-1-2-3

0 1 2 3

2 3

3 3

Ф 1 2 3

2 3

3 3

0 1 2 3

В классе r=1 – нет никаких вакансий

r=2 - 0-1, 0-2, 0-3, 1-2, 1-3, 2-3

r=3 - 0-1-2, 0-1-3, 0-2-3, 1-2-3

r=4 - 0-1-2-3

3. синтез комплексных прогнозов – отбор оптим. Комбинированного прогноза

Исключения частных прогнозов:

1. исключению подлежат все варианты, для кот, коэф-т согласованности >25

2. если дуги не заканчиваются в конечной вершине, то и все последующие модели исключаются.

Противоречивые комбинации: 1-3, 1-2-3, 0-1-2-3, 0-1-3.

3)исключаются дуги, связанные с рассогласованными комбинациями.

50. СИНТЕЗ ПРОГНОЗНЫХ АЛЬТЕРНАТИВ С УЧЕТОВ «ВЕСА» ЧАСТНЫХ ПРОГНОЗОВ. ОЦЕНКА ТОЧНОСТИ КОМПЛЕКСНОГО ПРОГНОЗА( НА ПРИМЕРЕ ПРОГНОЗА КЛАССА R=3)

Формирование комбинированно прогноза с учетов веса частных прогнозов:

У_r^k=

Последовательно формируются комбинированный прогноз для всех возможных вариантов по каждой оси r.

λ_rt=

Сумма всех весов=1.

Веса прогнозов формируются и определяются исходя из минимума дисперсии комбинированного прогноза.

σ_y=

Пример расчета для класса r=3:

Граф вариант

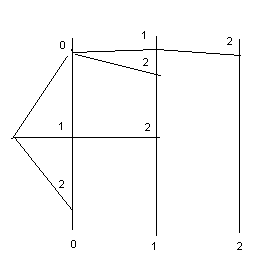
λ

Комбинированный прогноз:

Y(r=3)=

₃=

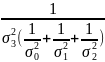
Дисперсия:

Д=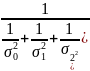

51. СИНТЕЗ КОМПЛЕКСНОГО ПРОГНОЗА ДЛЯ КЛАССА R=4 (СОСТАВИТЬ ГРАФ ВАРИАНТ С ОБЩИМ ЧИСЛОМ СОГЛАСОВАННЫХ ЧАСТНЫХ ПРОГНОЗОВ, РАВНЫМ 4)

Пример расчета для класса r=4:

Граф-вариант:

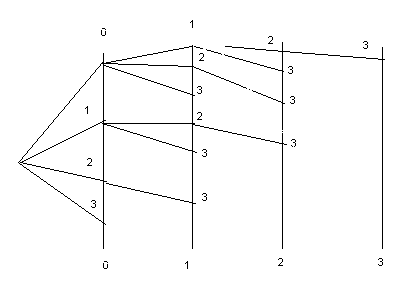
λ₄=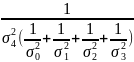

Дисперсия:

Д=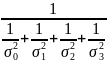

Комбинированный прогноз:

Y(r=4)=