41. Ошибки в одномерном прогнозе можно оценивать шестью способами:

●         Среднее абсолютное отклонение (MAD)

Среднее абсолютное отклонение, или просто среднее отклонение (MAD – mean absolute deviation) — величина, используемая для оценки прогнозных функций:

●         Средняя абсолютная процентная ошибка (MAPE)

●         Средняя квадратичная ошибка (MSE)

●         Корень средней квадратичной ошибки (RMSE)

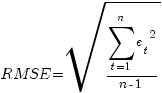
●         Средняя процентная ошибка (MPE)

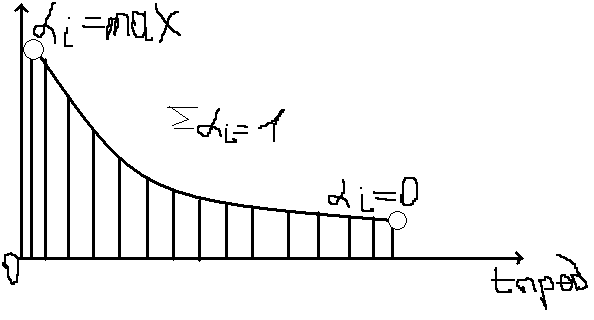
Неопределенность прогноза связана с невозможностью абсолютно точно предсказать будущее и отклоняемыми от действительных значений от прогнозных. Чем на большее кол-во лет разрабатывается прогноз, тем больше неопределенность.

На современном этапе для оценки неопределенности прогнозов используют вероятностный подход и рассчитанные на этой основе вероятностные характеристики( дисперсия, мат. ожидание и т.д).

Неопределенность исходной информации, используемой для разработки прогнозов заключается в уменьшении ее ценности, с течением времени, а также с наличием разного рода нарушений в данных.

Учет неопределенности исходной информации уменьшает неопределенность прогноза. Существуют 3 основных метода оценки неопределенности прогноза:

1. Метод числовых моментов, который заключается в след.: определение мат. ожидания, дисперсии, среднеквадр. отклонения, коэфф. ассиметрии и эксцесса.

2. Метод симметричной апроксимации. Расчет основных характеристик на основе заранее заданных вероятностных законах. Как правило, нормального закона распределения, равномерного и бетта-распределения.

3. Метод Монте-Карло. Многократное использование прогнозной модели для данных, искаженных в соответствии с различными вероятностными законами и оценкой выходной характеристики, такой модели по наилучшему вероятностному закону.

Оценка неопределенности исходной информации с учетом «веса» информации прогнозирующих моделей.

42.Недостатки коэф. Корреляции и деерминации. Способы их преодоления. Скорректиррованныйкоф. Детерм. Автокорел. Остатков прогнозных моделей

Недостатки:

1.знач. коэф. корел. и детерм. не уменьшается при увеличении кол-ва прогнозной модели

2.коэф. корел. и детерм.могут показывать сложную взаимосвязь между переменными,если эти переменные синхронно изменились

Для преодоления атокорел. остатков прогнозных моделей исп-ют дополн. критерии:

1.скоректированный коэф. Кореляции

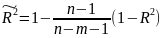
2.статистика Дарбина-Уотсона(DW стат.)-исп-ся для проверки автокореляции остатков прогнозных моделей.Значение должно лежать [0;4]

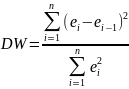
Если - сильная положительная автокор.остатковпрогн. моделей

- сильная отрицательнаяавтокор.остатковпрогн. моделей

[1,5;2,5]-модель изначально подобрана правильно

Скорректированный коэффициент детерминацииисп-ся для того, чтобы была возможность сравнивать модели с разным числом факторов так, чтобы число регрессоров (факторов) не влияло на статистику

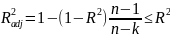
n — количество наблюдений, а k — количество параметров

Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля.

43.Причины появления автокор.Остатковпрогн.Модели и способы её обнаружения.Расчет статистики Дарбина-Уотсона.Преодолениеавтокор.Остатков и прогнозных моделей.

Автокорреляция остатков чаще всего наблюдается тогда, когда эконометрическая модель строится на основе временных рядов Автокорреляция может быть также следствием ошибочной спецификации эконометрической модели. Кроме того, наличие автокорреляции остатков может означать, что необходимо ввести в модель новую независимую переменную.

Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных.

Автокореляцию можно определить с помощью графического метода,метода рядов,критерияДарбина-Уотсона,теста серий (Бреуша-Годфри),тестаЛьюинга-Бокса.

Для преодоления атокорел. остатков прогнозных моделей исп-ют дополн. критерии:

1.скоректированный коэф. Кореляции

2.статистика Дарбина-Уотсона(DW стат.)-исп-ся для проверки автокореляции остатков прогнозных моделей.Значение должно лежать [0;4]

Если - сильная положительная автокор.остатковпрогн. моделей

- сильная отрицательная автокор.остатковпрогн. моделей

[1,5;2,5]-модель изначально подобрана правильно

44. Интеллектуальные технологии в прогнозировании. Этапы генетического алгоритма направленного отбора вариантов адаптивных прогнозных моделей и расчет количества уравнений на каждом этапе. Формирование обучающей и контрольной последовательностей. Расчет критерия качества адаптивного прогноза.

Адаптивные методы получили свое название в силу использования заимствованных у природы механизмов самоорганизации. Различают : адаптивнные методы, направленного подбора устранения полного перебора вариантов прогнозных моделей; самообучающиеся методы(нейронные сети).

Алгоритм заключается в подстройке весов на входе модели с целью минимизации ошибки на выходе. Такие методы не требуют набора экзогенных факторов. Генетические алгоритмы- алгоритмы поиска лучших, оптимальных или рационал. решений , построенных на принципах, сходных с принципами естественного отбора и генетики. Они определяют принцип выживания наиболее перспективног решения и структурированный случайный детерминированный обмен информацией, в кот. присутстувуют элементы случайности, моделирующий природные процессы наследования и мутации.

5

4

3

П

1

2

6

результат

од рациональным решением понимают решения, которы удовлетворяют исследователям и соответстветствуют определенным ограничениям.

I этап

н е выполн.

нет II этап

III этап

да

1. Создание начального множества прогнозных моделей;

2. Отбор лучших прогн моделей и факторов;

3. Случайно детерминированные изменения спецификаций прогнозных моделей;

4. Создание новых множеств прогнозных моделей;

5. Случайные изменения специфик прогнозных моделей;

Результат-оптимальное или рациональное решение

Схема раб. метода направленного выбора вариантов прогнозных моделей. Цель: поиск спецификации прогнозных моделей оптимальной сложности. Такая схема работы применяется для большого количества факторов(до 100 ф-ров одновременно).

Схема применения: 1) поиск наилучшей спецификации прогнозной модели производится на основе перебора всех возможных вариантов с алгоритмом наискорейшего спуска к оптимуму; 2) кол-во критериев устанавливается симметрично количеству преследуемых целей.

Первым критерием является минимум суммы квадратов ошибок модели; вторым- мера неопределенности прогноза, вычисленная с использованием модели и измеренная через среднеквадратическое отклонение прогнозных значений от действительных :

С реднеквадратическое отклонение вычисляется на контрольной последовательности данных

ретроспекция проспекция

Обуч. Контрл.

последовательность посл-сть

N_k N_k^’

N_k= (0,6 – 0,75) N; N_k^’=(0,25 – 0,4)N

Среднеквадратическое отклонение используется для отбора оптимальной прогнозной модели и может применяться в абсолютной и относительной форме.

3) Существует оптимум сложности спецификации прогнозной модели. Дальнейшие усложнения модели не дают эффекта.

4) Существует оптимальный набор факторов, обеспецивающих оптимальную точностьпрогнозирования.

Этапы генетического алгоритма направленного отбора вариантов адаптивных прогнозных моделей:

1. Каждый экзогенный фактор х из набора рассматривается по отдельности с целью выявить наиболее значимые для решения заданного прогноза с учетом возмоможных модификаций связей прочности уравнения.

2. Отбирается наиболее значимые факторы, имеющие минимальные среднеквадратические отклонения, которые ,как правило, имеют 60% общего количества исследуемых параметров. Тем самым реализуется механизм естественного отбора.

3. Отбираются комбинации, являющиеся наилучшими по заданному критерию ξ

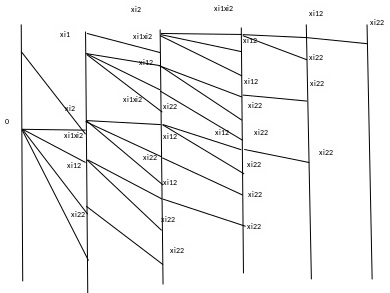
45.ГРАФ ВАРИАНТОВ НА ОСНОВЕ ПОЛИНОМИАЛЬНОЙ ПРОГНОЗНОЙ МОДЕЛИ ПРИ П_{ЗНАЧ.ФАКТ.}=1, П_ПОЛИН=4. ВАРИАНТЫ ПРОГНОЗНЫХ УРАВНЕНИЙ. РАСЧЕТ ПРОГНОЗНЫХ КОЭФФИЦИЕНТОВ НА ОСНОВЕ МНК (НА ПРИМЕРЕ КОНКРЕТНОГО УРАВНЕНИЯ).

Составлен граф вариантов у₀= а₀+ а₁ х₁+ а₂ х₁²+ а₃ х₁³+ а₄ х₁⁴

46.ГРАФ ВАРИАНТОВ НА ОСНОВЕ ПОЛИНОМИАЛЬНОЙ ПРОГНОЗНОЙ МОДЕЛИ ПРИ П_{ЗНАЧ.ФАКТ.}=2, N_ПОЛИН=2. ВАРИАНТЫ ПРОГНОЗНЫХ УРАВНЕНИЙ. РАСЧЕТ ПРОГНОЗНЫХ КОЭФФИЦИЕНТОВ НА ОСНОВЕ МНК (НА ПРИМЕРЕ КОНКРЕТНОГО УРАВНЕНИЯ).

У= а₀+а₁ х_i1+а₂х_i2+а₃х_i1х_i2+а₄х_i1²+а₅х_i2²