33.Треб-я исх. Инфо.Типы исх.Данных. Модели поведения данных,представляемые временными рядами.

Треб-я, удовлетв.исх.данным:

1)Случайные ошибки должны иметь случайные вел-ны и пост.дисперсию. 2)случ.ошибки не должны коррелировать с независ. наблюд.; 3)дисперсии случ.ошибок должны быть одинак; 4)знач.ошибок различных наблюд. не должны автокоррелировать; 5)случ.ошибки должны иметь норм. распределение.

34. Аналитическое представление моделей поведения данных временных рядов. Задачи анализа моделей поведения данных.

Под временным рядом (динамическим рядом, или рядом динамики) в экономике подразумевается последовательность наблюдений некоторого признака (случайной величины) Y в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда, которые будем обозначать y_t(t=1,2,..,n) где n - число уровней.

Отметим основные этапы анализа временных рядов:

- графическое представление и описание поведения временного ряда;

- выделение и удаление закономерных (неслучайных) составляющих временного ряда (тренда, сезонных и циклических составляющих);

- сглаживание и фильтрация (удаление низко- или высокочастотных составляющих временного ряда);

- исследование случайной составляющей временного ряда, построение и проверка адекватности математической модели ее описания;

- прогнозирование развития изучаемого процесса на основе имеющегося временного ряда;

- исследование взаимосвязи между различными временными рядами.

Временной ряд можно изобразить графически

спрос

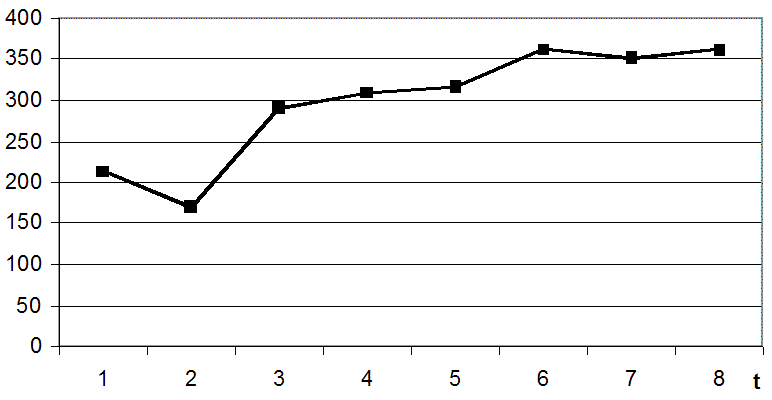год

Ряды динамики бывают моментными и интервальными. Ряд динамики называется моментным, если значения показателя фиксируются по состоянию на определенные моменты времени (определенные этапы), например запасы разведанных полезных ископаемых на конец года, уровень производительности труда, достигнутый к концу года, ОПФ к началу года и т. д.

Интервальным называется ряд динамики, в котором значения показателя характеризуют результаты, полученные за определенные промежутки времени - интервалы, например прибыль, полученная за 1980, 1981,…, 1990 гг.

35. Исследование данных временных рядов на основе автокорреляционного анализа. Определение автокорреляции и авторегрессии. Расчет параметров автокорреляционной функции и оценка значимости коэфф акф.

АК-завис или сила связи м/д переменной y(t),харак прогнозир показатель, и переменными этого же показателя y(t-1),y(t-2),…,y(t-k), смещ относительнол y(t) на периоды t-1, t-2…

k- временная сдвижка или лаг.

АКФ- последовательность знач. коэф.АК, вычисл. для различ периодов запаздывания.

В общем случае АКФ наз корреляционной.

2

1-сильная АК зависимость

2-средня АК зав-ть

3-слабая АК зав-ть

4-сильная периодич АК зав-ть

Авторегрессия- предст собой приема регрес анализа для усн вида связи м\д переменной y(t), характериз прогноз показатель и перемен этого показ y(t-1),.., смещ относ y(t) на перемен (t-1), …или, другими словами м\д рез очередного и предыдущих испыт одного и того же процесса.

АК компоненты м. входить в регресс завис общего вида.

Для построения АКФ коэф АК рассчитывают для различ сдвижек по ф:

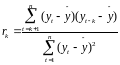
n-кол-во точек временного ряда

y_t – значение временного ряда в момент времени t

y_t-k- значение времен ряда в мом вр t-k

k- лаг

- среднее значение вр ряда

Для определения границ значимости АК исп понятие стандарт ошибки:

Интервал значимости

t-параметр довер вер., зав от длины исх. ряда и уравнения довер вер.

Если значение АК выходят за границы то они явл высокозначимыми.

36. СВОЙСТВА АВТОКОРРЕЛЯЦИОННЫХ ФУНКЦИЙ. ГРАФИКИ АКФ ДЛЯ ОСН МОДЕЛЕЙ ПОВЕДЕНИЯ ДАННЫХ И СЛУЧАЙНЫХ ДАННЫХ. ПОНЯТИЕ ЧАСТНОЙ АКФ. ПРИНЦИПЫ ВЫБОРА МЕТОДОВ ПРОГНОЗИРОВАНИЯ НА ОСНОВЕ АВТОКОРР АНАЛИЗА ДАННЫХ.

Св-ва АКФ:

• явл убывающей;

• при к=0 принимают предельное значение;

• явл четной;

• АКФ стац случ процесса, на кот налож периодич сост также будет содерж периодич сост той же частоты;

• чем слабее взаимосвязь м\д знач переменными ряда, тем быстрее убыв АКФ.

Т рендовая модель Стационарная модель

С езонная модель Циклическая модель

Порядок выбора методов прогнозирования на основе АК анализа данных:

1. Построить график изм динамики прогноз показателей.

2. Рассчит знач АКФ построить график.

3. По виду графика и о исп числ знач АКФ определить модель поведения данных.

4. На основании установл модели поведения данных треб-го периода упреждения и длины временного ряда подобрать наиб приемл метод прогнозирования.

5. Если АК в данных им-ся и учесть АК не предст возм., необх использовать в прогноз моделях авторегрес-е состав-щие или авторегрес модели.

Частная АКФ- очищенная АКФ от связей м/д переменными на вр сдвижках, отличных от исследуемых.

37. ПРОГНОЗИРОВАНИЕ ТРЕНДА ОСНОВНЫХ ПОКАЗАТЕЛЕЙ РАБОТЫ ТРАНСПОРТА НА ОСНОВЕ РЕСРЕССИОННОГО АНАЛИЗА. ЭКСПОНЕНЦИАЛЬНАЯ МОДЕЛЬ ТРЕНДА РОСТА ОБЩЕГО ГРУЗООБОРОТА НА ТРАНСПОТРЕ ВИДА Г_I = Е^{(А0+ А1 TI)} + Ε. РАСЧЕТ СЧЕТ ПРОГНОЗНЫХ КОЭФФИЦИЕНТОВ НА ОСНОВЕ МНК И ПРОГНОЗ ИЗМЕНЕНИЯ ТРЕНДА.

По своему значению регрессионный анализ:

-однофакторный

-парная регрессия

-множественная регрессия

Общий вид – y = F(x) + ε

где y – прогнозируемая(зависимая) переменная;

F(x) – статистическая зависимость, называемая функцией регрессии у по х и описывающая изменение условного среднего значения результирующего показателя у в зависимости от изменения значений, объясняющих экзогенную переменную х;

ε - величина случайной ошибки.

Основные этапы прогнозирования на основе регрессионного анализа:

1. Сбор данных

2. Изучение структуры данных

3. Выбор метода прогнозирования и разработка прогнозной модели

4. Прогнозирование прошедших периодов

5. Проверка точности и расчет критерия качества

6. Прогнозирование будущего и выработка упрощенного рещения

7. Периодическая проверка точности прогнозирования на действительных значениях

8. Проверка точности прогнозов

9. Добавляем новые данные и возвращаемся к новому этапу(если не прошла проверка)

Для расчета прогнозных коэффициентов использу метод наименьших квадратов(МНК), согласно которому:

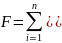
где – F – функционал рассогласования действительных значений показателя и прогнозных значений ;

n – количество точек динамического ряда показателей.

Для случая экспоненциальной зависимости:

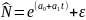
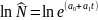
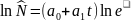
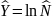
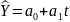
Коэффициенты модели:

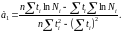
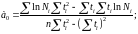
Система нормальных уравнений:

38. НЕОПРЕДЕЛЕННОСТЬ ИСХОДНОЙ ИНФОРМАЦИИ. МЕТОДИКА ОЦЕНКИ «ВЕСА» ИНФОРМАЦИИ В ПРОГНОЗНЫХ МОДЕЛЯХ И РАСЧЕТ ВЕСОВЫХ КОФФИЦИЕНТОВ. ЭКСПОНЕНЦИАЛЬНАЯ ТРЕНДОВАЯ МОДЕЛЬ ОБЩЕГО ГРУЗООБОРОТА НА ТРАНСПОРТЕ С УЧЕТОМ ВЕСА ИСХОДНОЙ ИНФОРМАЦИИ.

Вследствие неопределенности исходной информации, положенной в основу принятия решений, рекомендуется анализ вариантов и их оценку производить для различных альтернатив исходных показателей. Весовые коэффициенты могут определятся различными способами. Как правило используют экспоненциальный закон изменения информации.

α

α_max

Σα_i=1

t_пред t

Для расчета весовых коэффициентов используют формулы:

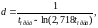
где t_i – периоды времени, которые соответствуют i-му наблюдению прогнозируемого показателя;

t_пред – максимальная длина временного ряда, в течение которого наблюдения временного прогнозного показателя значимы.

Э кспоненциальная трендовая модель общего грузооборота БЧ с учетом «веса» исходной информации будет иметь следующий вид:

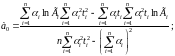
39. Прогнозирование транспортных процессов методами множественной регресии. Двухфакторная регрессионная модель тренда вида у_i=a₀+a₁x_1i+a₂x_2i+ε . Расчет прогнозных коэффициентов на основе МНК.

Этапы составления прогнозных моделей:

1. Изучение связей между зависимым фактором у и независимым фактором х.

2. Изучение связей между независимыми функциями х.

3. Выбор значимых факторов для изучения модели.

4. Расчет влияния каждого фактора на величину у.

5. Составление прогнозного уравнения.

6. Расчет коэффициентов модели.

у=a+b₁x₁+b₂x₂+ε,

где а, b₁ и b₂ – определяются по методу наименьших квадратов.

Силу значимости определяют по коэффициентам корреляции.

Коэффициенты парной корреляции:

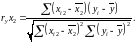
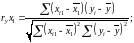
40. Коэффициент корреляции рассчитывается следующим образом:

Есть массив из n точек {x_1,i, _x2,i}

Рассчитываются средние значения для каждого параметра: 

И коэффициент корреляции: 

r изменяется в пределах от -1 до 1. В данном случае это линейный коэффициент корреляции, он показывает линейную взаимосвязь между x₁ иx₂: r равен 1 (или -1), если связь линейна.

Коэффициент r является случайной величиной, поскольку вычисляется из случайных величин.

Для оценки качества модели используют коэффициент детерминации. Долю дисперсии, которая обусловлена регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R2.

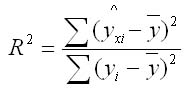
Коэффициент детерминации, как и коэффициент корреляции, принимает значения от -1 до +1. Чем ближе его значение коэффициента по модулю к 1, тем теснее связь результативного признака Y с исследуемыми факторами X.

Величина коэффициента детерминации служит важным критерием оценки качества линейных и нелинейных моделей. Чем значительнее доля объясненной вариации, тем меньше роль прочих факторов, и значит, модель регрессии хорошо аппроксимирует исходные данные и такой регрессионной моделью можно воспользоваться для прогноза значений результативного показателя.

Скорректированный коэффициент детерминации и статистика Дарбина-Уотсона используются для преодоления автокорреляции остатка прогнозных явлений:

Скорректированный коэффициент детерминации:

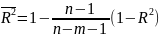
Статистика Дарбина-Уотсона:

DW=

DW статистика используется для проверки автокорреляционных остатков прогнозных моделей. Значение статистик должно лежать от 0 до 4.

Если DW~0 – то имеется сильная положительная автокорреляция остатков прогнозных моделей

Если DW ~4 – то наблюдается сильная отрицательная автокорреляция

Оптимальное значение [1,5; 2,5].