12. Интеграл Римана как предел интегральных сумм. Интегрируемость непрерывной функции. Формула Ньютона – Лейбница. Интеграл Лебега. Свойства интегралов Римана и Лебега.

Задачи, привод.к опред.интегралу.

Зад.1. вычислить площадь криволин.трапеции.

о .1. фигура Ф={(x,y) назыв.криволин.трапецией, если это мн-во непусто и f(x)-непрерывна на [a,b].

Замеч: чтобы Ф нужно a<b и f(x) 0, но хотя бы в одной точке f(x)>0.

1)разобъем [a,b] на n-произвольных частей точками, получим T: a=x₀<x₁<…<x_n=b; 2) На каждом частичном пром-ке [x_i-1;x_i], i= выберем произв.точку и обоз-м _i [x_i-1;x_i]. полученное разбиение наз-ся отмеченным и обоз-ся T. 3) найдем зн-е ф-ции y=f(x) к каждой выбранной точке f( _i). 4) построим ступенч.фигуру, представл.собой объединение прямоуг-ов с основаниями [x_i-1;x_i] и высотами f( _i). 5) площадь ступенч.фигуры равна: , x_i - x_i-1. 6) обозн.через =max , i= - диаметр разбиения T. 7) назовем площадью криволин.трап.: S= .Этот предел сущ-т и не завис.от способа разбиения отрезка [a,b] на части, ни от выбора точек _i.

Зад.2. масса неоднор.стержня

Пусть зад.неоднор.стержень, располож.вдоль числов.оси на пром-ке (a,b) и пусть пл-ть стержня есть величина переменная и завис.от коорд-ты каждой точки стержня и зад-ся функцией y= .

0 a x_{i-1 i} x_i b

1)введ.разбиение T:a=x₀<x₁<…<x_n=b; 2) введ.отмечен.разбиение : _i [x_i-1;x_i]. 3)найдем зн-е ф-ции в этих точках _i) и предп.что на всем пром-ке [x_i-1;x_i] пл-ть стержня будет постоянна и равна _i). 4) m . 5)введ. =max . 6) массой неоднор.стержня наз-ся m= , если этот предел сущ-т и не завис.от отмечен.разбиения.

Понятие опред.интеграла. Необх.усл-е его сущ-я.

Пусть на отр. [a,b] зад.функция y=f(x).

1)постр.разбиен.T:a=x₀<x₁<…<x_n=b; 2)выберем отмеч.разбиение : _i [x_i-1;x_i].

3) нах.зн-е ф-ции в отмеч.точках f( _i). 4) строим .

о.1. наз.интегральн.суммой ф-ции f(x) для дан.отмечен.разбиения.

5) назовем =max , i= .6) вычисл.предел .

0.1. если предел интегр.сумм сущ-т и не завис.от выбора отмечен.разбиения, то этот предел наз-ся определ.интегралом функции f(x)на отр.(a,b)

𝒥 x:= , что означ. ( следует ).

Геом.смысл интеграла: Для неотр.ф-ции на [a,b] опред.интеграл-есть площадь криволин.трапеции(см.зад.1).

Физич.см.интеграла: масса неоднор.стержня(см.зад.2) или длина пройден.пути.

Теор.(Необх.усл-е сущ-я опр.интеграла)

Для того, чтобы ф-ция была интнгрируема на пром. [a,b] необх, чтобы она была ограничена на этом отрезке. Если ф-ция интегрируема, то она ограничена.

Док-во: (от противн)

Сущ-т (предел интегр.сумм). Предп-м, что ф-ция не огран.на [a,b], тогда для любого разбиения T сущ-т хотя бы один отрезок [x_i-1;x_i], в кот.ф-ция огран. Выберем произвольно _i [x_i-1;x_i], i= и постр.такую сумму: + =A.

Рассм-я разл. _k [x_k-1;x_k]всегда можно выбрать среди них такое, что произвольное f( _k) x_k =A+ , =max , тогда f( _k) x_k, тогда ; ,т.е. предел -не сущ-т. Значит, предпол.неверно и теор.док.

Замеч: огран-ть не явл-ся достат.усл-м интегрир-ти функции.

Суммы Дарбу.

0.1.пусть на отр. [a,b] ф-ция f(x) огран, тогда выберем какое-ниб.разбиение T:a=x₀<x₁<…<x_n=b и выб.отмечен.разбиение . Тогда т.к. f(x) огран, то f( _i)тоже огран.при всех i, тогда обозн-м через m_i=inf f( _i), M_i =sup f( _i).Тогда интнгр.суммы вида и наз-ся нижней и верхн.интегр.суммами или нижн.и верхн.суммами Дарбу ф-ции f(x) на [a,b] соотв-м разбиению Т.

Св-ва сумм Дарбу: 1)при данном разбиении Т справ-во нер-во s ,где s= , S= , -произв.интегр.сумма. Док-во: Т: m_i f( _i) M_i, , m_i f( _i) M_i

Просуммировав n-нер-в одинак.смысла, получим искомое нер-во.

2)при добавлении к разбиению Т новых точек дробления нижн.сумма Дарбу разве лишь увелич-ся, а верх.разве лишь уменьш. 3) пусть даны два разбиения Т₁ и Т₂, тогда нижн.сумма Дорбу первого разбиения ме6ньше или равна верхн.сумме второго разбиения. Всякая нижн.интегр.сумма не превосх.всякой верхн.интегр.суммы(независимо от разбиения). s₁ S₂. Док-во: добав.к разбиению Т₁ разбиение Т₂, число точек дробления разве лишь увелич.и обозначим новое разбиение Т₃. Тогда по (св-ву 2)s₁ s₃ S₃, добавление новых точек лишь уменьшит сумму по сравнению с предыдущей s₁ s₃ S₃ S₂.

Критерий интегрируемости функции.

Теор. Для того, чтобы ф-ция y=f(x) была интегрир.на отр.[a,b], необх.и дост,чтобы вып.усл-е: .

Док-во: I(необх.) f(x)-интегр.на [a,b], 𝒥 x= (

, ; справ.нер-во => 2 => .

II(дост-ть): : ( ;

) s , где -верхн.грань s, , -нижн.грань S, ;

, = , s ;

=>ф-ция интегрируема.

Достат.признаки интегрир-ти ф-ции.

Т.1.если ф-ция f(x) непрер.на отр.[a,b], то она интегрируема на этом отрезке.

Т.2. если ф-ция f(x)огран.на отр.[a,b] и им.кон.число точек разрыва, то она интегрируема на [a,b].

Т.3. если ф-ция f(x) монотонна и огран.на отр.[a,b], то она интегр-ма на этом отрезке.

Док-во: пусть для опред-ти ф-ция возрастает на [a,b]. Тогда ее колебания _k = M_k – m_k=f(x_k)-f(x_k-1). Пусть ( и , , тогда ))= => f(x) интегр.на [a,b].

Св-ва опред.интеграла.

1. ; 2) ;

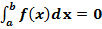3) ) ;

Док-во: пусть ф-ция f(x) интегр-ма на [a,b]. Рассм.такое разбиение Т отрезка [a,b],что с принадл-т этому разбиению Т.

, где в первую сумму входят слагаемые до точки с, а во вторую – после точки с.

= _i) _i) ; ;

Рассм.2-ой случай: ; =

4)Постоян.множит.можно выносить за знак интеграла. ;

=

6)если ф-ция f(x) неотриц.на [a,b](f(x) , то ;

7)f(x) , x

8) ; док-во: по 2св-ву модуля им.- ;

-

9) если функция f непрер.на [a,b], то m и M ее наим.и наиб.зн-е на этом отрезке, тогда справедливо нер-во: m(b-a)

10)(теорема о среднем):

Если ф-ция f(x) непрер.на [a,b], то справ-во рав-во: )(b-a), [a,b].

Док-во: (на основании 9св-ва)

m,M => m=minf(x), M=maxf(x); m(b-a) -поделим на (b-a) => m

Определ.интеграл с переменным верхним пределом.

Пусть f(x) непрер.на [a,b],т.е. тогда f(x) непрер.на любом отрезке [a,x], где [a,b] => интегр-ма на этом отрезке;

- интеграл с перемен.верхн.пределом. Обозн. Ф(x)=

Теор.: если f(x) непрер.на [a,b], то производная от интеграла с перем.верхн.пределом есть подинтегральн.функция в верхн.пределе интегр-я, т.е. ( (1)

.

Придадим x приращение . Построим ф-цию Ф( = положим, что = = заметим, что лежит между точками x и x+ и при

Формула Ньютона-Лецбница.

Пусть непрер.на [a,b]. Тогда сущ-т первообразная для этой ф-ции и обоз-м ее F(x),т.е. F׳(x)=f(x). Интеграл с переменным верхн.пределом ф-ции f(x) также явл.первооб-ой ф-ции, а по св-ву первообр.они могут отличаться лишь на произвольн.постоянную, т.е. Ф(x)-F(x)=C, тогда Ф(x)=F(x)+C; (1)

По св-ву опред.интеграла положим x=a и получим: ; (2)

Интеграл Лебега. Св-ва интегралов Римана и Лебега

Пусть f(x) ограниченная измеримая ф-ция, определенная на мн-ве ЕR, измеримом по Лебегу (внутр. и внеш. меры Леб. совпадают (_(А)=^(А), _(А)=sup m(F), FA, F- замкнуто; ^(А)=inf m(G), GA, G открыто)

[A,B]E(f), разобьем отрезок A=y₀<y₁<…<y_N=B. Рассмотрим мн-во Ek={xE| y_kf(x)<y_k+1}, k=0..N-1, E_N={xE| f(x)=y_N} – все эти мн-ва измер. по Леб.

Построим интегр. сумму _L(f,)=y_k(E_k), k=0..N, где  - мера Лебега на числ. пр-й.

Интегралом Лебега ф. f по мн-ву Е наз.

Т. Интеграл Лебега по мн-ву, измер. по Лебегу,  д/ ограниченной измеримой ф-ции.

Т. Если ф-ция интегрир. по Риману на [a,b], то она измер. на этом отр. и ее интеграл Римана и интеграл Лебега совпадают.