8. Тригонометрические функции.

Действительная область

y=sin x (нечетная); y=cos x (четная)

1. D(sin)=D(cos)=R 2. E(sin)=E(cos)=[-1,1]

3. y=sin x>0 при x(2n;+2n); y=sin x<0 при x(+2n;2+2n), nZ

y=cos x>0 при x(-/2+2n;/2+2n); y=cos x<0 при x(/2+2n;3/2+2n), nZ

4. T=2n, nZ

5. y=sin x  при x(-/2+2n;/2+2n), max=/2+2n;

y=sin x  при x(/2+2n;3/2+2n), min=-/2+2n, nZ

y=cos x  при x(-+2n;2n), max=2n; y=cos x  при x(2n;+2n), min=+2n, nZ

6. y=sin x=0 при x=n, nZ y=cos x=0 при x=/2+n, nZ

Теорема. Ф-ции y=sin x, y=cos x непрерывны на всей числовой прямой.

Д-во.

sin α<α, 0<α</2, |sin α|1, |cos α|1

1) |∆y|=|sin(x+∆x)-sin x|=2|sin ∆x/2||cos (x+∆x/2)|<2 |∆x|/2=∆x lim ∆y=0 (∆x0) y=sin x – непрерывна на всей числовой прямой

2) |∆y|=|cos(x+∆x)-sin x|=2|sin ∆x/2||sin (x+∆x/2)|<∆x lim ∆y=0 (∆x0) y=cos x – непрерывна на всей числовой прямой

y=tg x (нечетная); y=ctg x (нечетная)

1 . D(tg)=R\{/2+n}; D(ctg)=R\{n}, nZ 2. E(tg)=E(ctg)=R

3. y=tg x (y=ctg x)>0 при x(n;/2+n); y=tg x (y=ctg x)<0 при x(/2+n;+n), nZ

4. T=n, nZ

5. y=tg x  на D(y) y=ctg x  на D(y) точек экстремума нет

6. y=tg x=0 при x=n, nZ y=ctg x=0 при x=/2+n, nZ

Теорема. Ф-ции y=tg x, y=ctg x непрерывны на всей области определения.

Д-во. Следует из непрерывности частного непрерывных функций.

y=arcsin x

1. D(y)=[-1,1]

2. E(y)=[-/2,/2]

3. строго возрастает

y =arccos x

1. D(y)=[-1,1]

2. E(y)=[0,]

3. строго убывает

y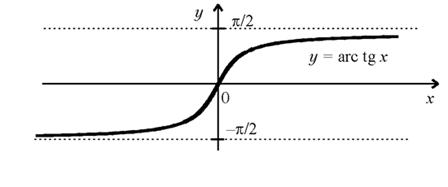 =arctg x

1. D(y)=R

2. E(y)=(-/2,/2)

3. строго возрастает

y =arcctg x

1. D(y)=R

2. E(y)=(0,)

3. строго убывает

Теорема. Обратные тригонометрические ф-ции непрерывны на всей области определения.

Д-во. Следует из непрерывности ф-ции, обратной непрерывной функции. ЧТД

Комплексная область

О: Назовем синусом комплексного числа z сумму ряда .

; tg z:=sin z/cos z; ctg:= cos z/sin z

Св-ва:

1. D(sin)=D(cos)=C

2. (sin z)’=cos z

(cos z)’=-sin z

Ф-ции sin и cos осущ. конформное отображение той части пл-ти, в к-рой соответствующая производная ≠0.

3. Справедлива ф-ла Эйлера: e^iz=cos z+i sin z

4. Сл-я из ф-лы Эйлера:

;

5. Справедливы все тригонометрические формулы

6. z₁≠z₂, sin z₁=sin z₂

2sin (z₁-z₂)/2 cos (z₁+z₂)/2=0

( z₁-z₂)/2=n или (z₁+z₂)/2=/2+k

z₁-z₂=2n или z₁+z₂=+2k, n,kZ

2 точки с одинак. ординатами, удовлетвор. 1 из этих уравнений, если расстояние м/у ними <.

Ф-ция не является однолистной. Максим. обл. однолистности – вертикал. полоса, шириной .

s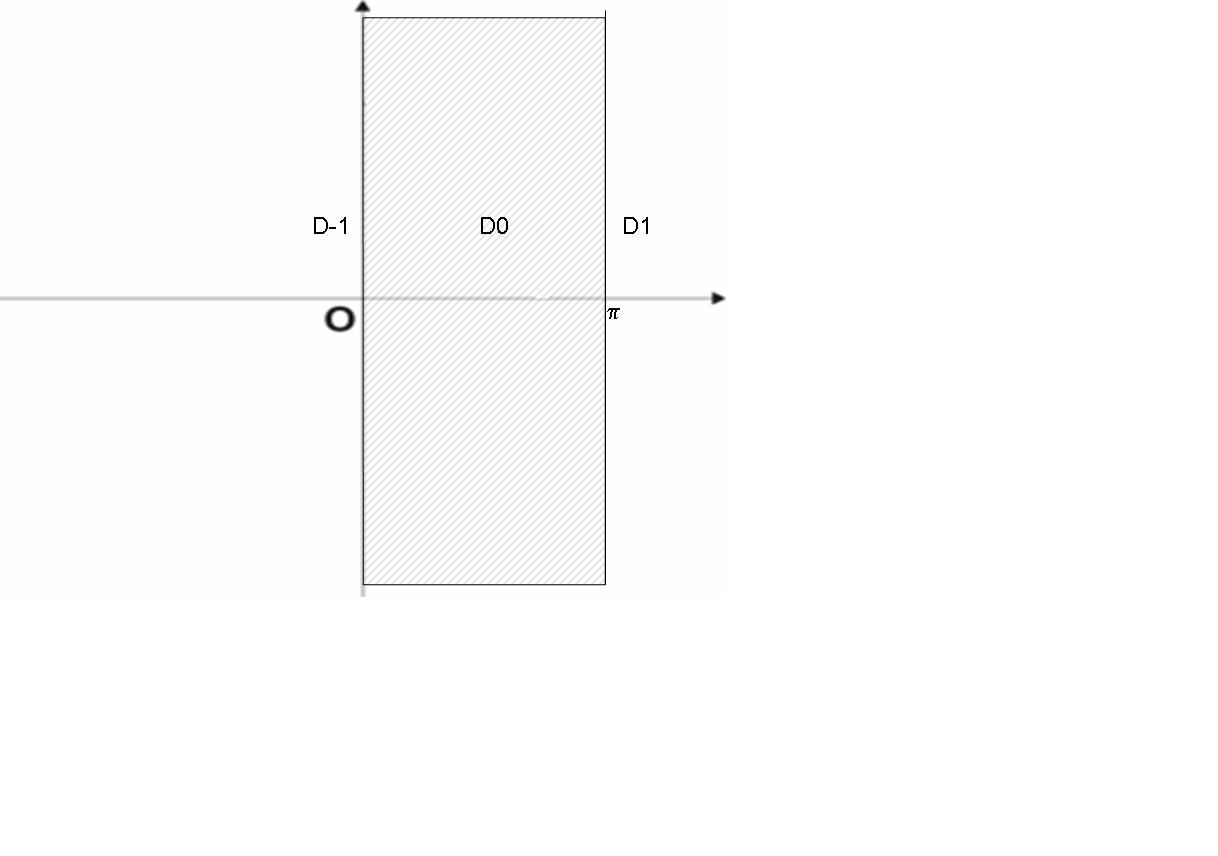 in z cos z

Обл. однолистности преобразуется во всю комплексную обл. с разрезами вдоль лучей u(-∞,-1],[1,∞) при v=0

Все обратные тр.ф. многозначные, чтобы превращать их в однозначные нужно строить Римоновы пов-ти их обл. определения.

Теорема об неограниченности sin x cosx в коплексной области:

=

О: Ф-ция w, удовлетвор. ур-ю z=sin w, наз. арксинусом и обознач. w=Arcsin z

e^iw=tt-(1/t)-2iz=0t²-2izt-1=0t=iz+√1-z²e^iw=iz+√1-z²iw=Ln(iz+√1-z²)

Arcsin z=(1/i)Ln(iz+√1-z²)

Arccos z=(1/i)Ln(z+√z²-1)

О: Ф-ция w, удовлетвор. ур-ю z=tg w, наз. арктангенсом и обознач. w=Arctg z

Arctg z=(-1/2i)Ln((i+z)/(i-z))

Arcctg z=(1/2i)Ln((z+i)/(z-i))