Вопрос 10.

10. Линейные операторы. Примеры и матричное представление. Матрицы линейных операторов в различных базисах. Собственные векторы и собственные значения линейного оператора.

О1: Всякая функция действ-я из V₁ в V₂ наз-ся оператором. О2: Оператор А:V₁→V₂ наз. лин-м операторам, если удовл. 2м усл. :1) (x_1,x₂  V₁) (A(x₁+x₂)=A(x₁)+A(x₂)), 2)(x₁  V₁) (A(αx₁)= αA(x₁))

О3: Оператор А: V → V наз. лин-м опер-м, если (x_1,x₂  V)(α,β  R)(A(αx₁+ βx₂)= αA(x₁)+ βA(x₂)) О4: Оператор А: V → V наз. лин. опер., если

1. (x_1,x₂  V) (A(x₁+x₂)=A(x₁)+A(x₂)) 2)(x₁  V) (A(αx₁)= αA(x₁))

V1=V2=V

Hom(V,V)=Hom(V) – мн-во лин. опер., действующих в пр-ве V

Примеры: A:R³R³

Все преобразования пл. в геом., кроме инверсий, есть лин. пр-ва

Свойства линейных операторов:

1 A*Ө=Ө 2 A(-x)= -Ax 3 (x₁,x_2,…,x_n  V)( α_1,α_2,…α_n  R)

(α₁ x₁+α₂ x₂+…+α_n x_n )= α₁Ax₁+α₂Ax₂+…+α_nAx_n

Представление лин. оператора матрицами.

О5: Матр. М_А наз. матр. лин. опера-ра А действ-го в пр-ве V в базисе (e₁,e₂,…,e_n) О6: Матр. в столбцах кот. расп-ны координаты образов соотв-х базисных векторов в дан. базисе наз. матр. лин. опер-ра в дан. базисе.

Очевидно, что д/дан.о лин. опер. с данным фиксир базислм !Mat_nR. Всякую Mat_nR можно считать матрицей только 1 лин. опер. Между Hom(V) и Mat_nR есть связь, это соответствие явл. однозначным.

AHom(V), dimV=n<

e1,e2..en – базис V «старый»

e’1,e’2..e’n – базис V «новый»

Разложим новый базис по старому

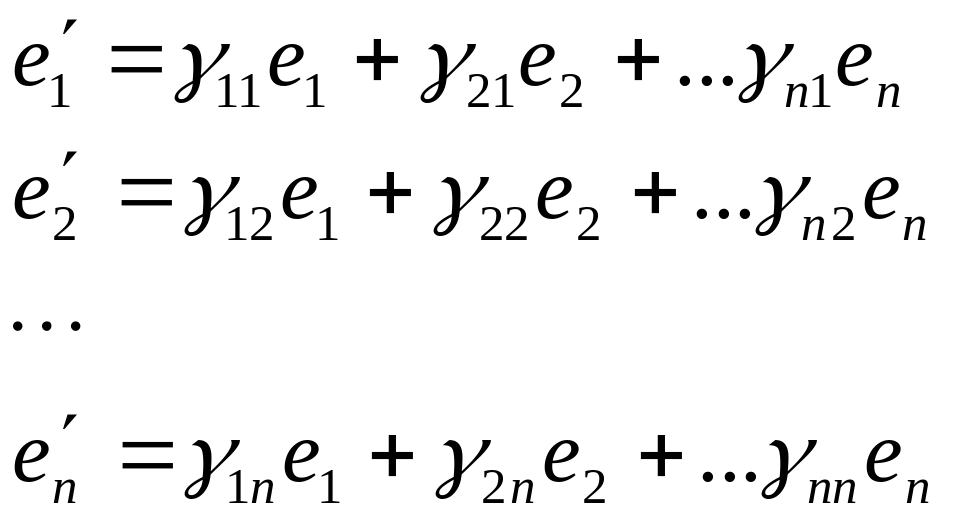
T=((e’1) (e’2) .. (e’n))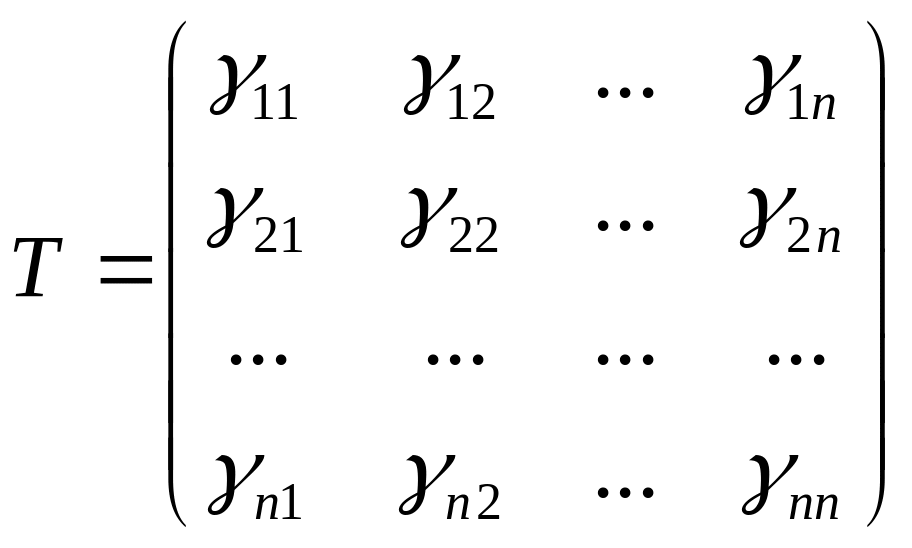

О7: Матрица Т наз.матр. перехода от старого базиса к новому.

Операции над линейными операторами и их матричные описания.

О8: Произведением лин. оператора А на действ. число α наз. опер. Обозн-й как αA и определяемый рав-ом (x  V)((αA)x=α(Ax)).

О9: + лин-х опера-в А и В действ-х в пр-ве V (dimV=n<∞) наз. опер-р обозн-ый А+В действующем в V и опред-ый рав-вом (x  V)((A+В)x=Ax+Вx).

О10: * лин. операторов А и В действ-х в пр-ве V (dimV=n<∞) наз. оператор обозначаемый А*В действ-й в V и опред-ый рав-ом(x  V)((A*В)x=A(Вx)).

Т: Пусть А,В  Hom(V), dimV=n<∞ тогда αАHom(V); αR; (А+В) Hom(V); (А*В) Hom(V);

Основные свойства: A,B,C  Hom(V); α,β  R;

1. (α+β)A=αA+βA; 2)(αβ)A=α(βA); 3)1*A=A; 4)(-1)*A= -A

5)0*A=0;6)A+B=B+A; 7)A+(B+C)=(A+B)+C;

8)A+0=A; 9)A+(-A)=0; 10)α(A+B)= αA+Αb;

11)A*(B*C)=(A*B)*C;12) a) A(B+C)=A*B+A*C; б) (A+B)*C=A*C+B*C;

Собственные значения и собственные векторы линейного оператора.

О11: Не 0й вектор х пр-ва V наз. собственным вект. лин. оператора А если (λ  R)(Ах=λх) при эт. число λ наз-ся собственным знач-ем опер-ра А, соотв-ий знач-ю собств-го вектору х.

О12: Характеристическим мног. (уравнением) лин. опер-ра А наз. характер-ий мног. (уравнение) люб. матр. лин-го опер.А.

О приводимости матрицы линейного оператора к диагональному виду.

Если матр. в нек. базисе пр. им. диагон. вид, то про л.оп. гов., что его мат. приводима к диагон. виду.