5) Выпуклость графика функции, точки перегиба

Пусть f(x) дифференцируема в каждой точке на (a,b)

График функции имеет выпуклость вверх(вниз), если график функции лежит не ниже (не выше) любой касательной (хорды) в точках абсциссы, к-рые (a,b)

M(x₀,f(x₀)) - точка перегиба графика функции, если существует такая U(x₀), в пределах которой график имеет разные направления выпуклости слева и справа от точки x₀

Т(Необходимое условие точки перегиба) Пусть f(x) дважды непрерывна дифф. на (a,b) , если x₀ - точка перегиба графика f(x), то

Т(Достаточное условие точки перегиба) Пусть f(x) имеет в некоторой окружности точки x₀, , тогда если в пределах указанной окрестности имеет разные знаки слева и справа от точки x₀ , то график функции имеет перегиб в точке x₀

Т(2 Достаточное условие точки перегиба) Пусть f(x) трижды дифф. в точке x₀ и , если , то x₀ – точка перегиба

Т(3 Достаточное условие точки перегиба) Пусть f(x) обладает производными до n-го порядка в и f⁽ⁿ⁺¹⁾ в точке x₀ , где - некоторое четное число, и пусть f(x₀)=…= f⁽ⁿ⁾(x₀)=0 , а f⁽ⁿ⁺¹⁾ (x₀) 0 , тогда x₀ – точка перегиба графика функции f(x)

6) Экстремумы функции нескольких переменных

Пусть z= f(x₁ , x₂…x_n) определена в некоторой области D

Точка наз-ся точкой max(min) функции f , если существует , такая, что вып-ся неравенство: f(x₁ , x₂…x_n) ( )

Т(Необходимое условие) Пусть f(x₁ , x₂…x_n) имеет в точке конечные частные производные , тогда для того , чтобы f имела в точке экстремум необходимо, чтобы все частные производные в этой точке =0

Т(Достаточное условие экстремума 2-х переменных ) Пусть f(x,y) определена, непрерывна и обладает непрерывными частными производными первого и второго порядка в некоторой окрестности стационарной точки (x₀ ,y₀). Пусть , , , тогда если AC-B²<0, то f не имеет экстремума в точке (x₀ ,y₀)

Вопрос 9.

Системы линейных уравнений. Понятие о частном и общем решении. Равносильность систем. Классификация систем по количеству решений. Теорема Кронекера – Капелли. Способ Гаусса решения систем линейных уравнений.

О1: Сист.m лин. ур-й с n неизвестными x₁, x₂,…,x _n над полем R наз. системой уравнений вида:

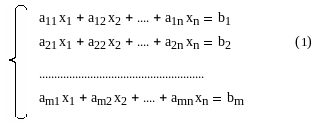
где a_ij  R ( i=1,…,m; j=1,…,n) наз. коэф-ми при неизв-х х_j. Действ-е числа b_i наз-ся свободными чл-ми.

, , …, , ,

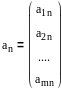где а₁, а_{2, …,} а_n, b – m-мерные арифметические векторы, а₁, а_{2, …,} а_n, b  R^m.

(2) – векторная запись линейных уравнений (1).

О2: Реш-ем СЛУ (1) наз. n-мерн. арифм. вектор (α₁, α₂,…, α_n) Rⁿ, если при подстановке в кажд. ур-е сист вместо неизв. х_j , j=1,…,n, α_j R,уравн-е превращается в верное числовое рав-во. О3: СЛУ наз однородной, если все своб.члены =0, в прот. случае слу наз. неоднородной. О4: СЛУ наз.совместной, если она имеет хотя бы 1 реш-е и несовместной в прот. случае. О5: СЛУ наз. определенной, если она имеет только 1 реш-е, и неопределенной, если она имеет >1го реш-я.

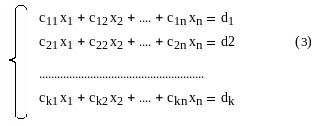
О6: Элементарными преобразованиями СЛУ наз.след. преобр-я:

1. перестановка местами люб. 2х ур-й сист; 2)* люб. ур-я системы на люб. действ. число, отличное от 0; 3)+ к люб. ур-ю сист. люб. др., умнож-го на люб. действ. число; 4)вписывание или вычеркивание из сист. ур-й вида: 0x₁ + 0x₂ + … +0x_n = 0.

О7: СЛУ наз. ступенчатой, если ее расширенная матр. явл. ступенчатой.

1. Если в ступенчатой СЛУ число ур-й = числу неизв-х, то сист. им. 1ое реш-е, т. е. явл. определенной.

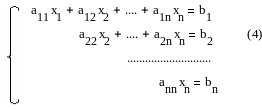а_ii ≠ 0, i=1,…,n

2. Если в ступенчатой СЛУ число уравн-й r меньше числа неизв-х n, то сист. имеет бесчисленное мн. реш-й, т. е. явл. неопределенной, при этом в системе линейных уравнений r главных неизвестных, n – r свободных неизвестных.

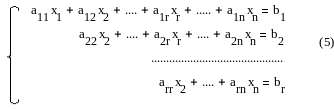а_ii ≠ 0, i=1,…,r

3. Если в ступенчатой системе линейных уравнений содержится уравнение вида 0x₁ + 0x₂ + … + 0x_n = b_n , b_n ≠ 0, то она не имеет решений, то есть является несовместной. Две несовместные системы равносильны.

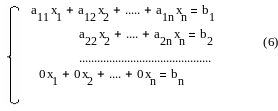b_n ≠ 0, а_ii ≠ 0, i=1,…,n

Идея метода Гаусса

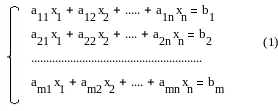
Путем элементарных преобразований привести систему линейных уравнений к равносильной ей ступенчатой СЛУ: (4) или (5) или (6) и п.2.

В рез.преобр-й у нас послед-но произойдет исключ-е неизв-х: из 2го ур-я (а_n ≠ 0) мы исключим x₁, из 3го ур-я – x₁ и x₂ и т.д. в рез. таких преобр-й число ур-й в получ-й СЛУ равносильной дан. м. только уменьш-ся или остаться таким же числом, но не увел-ся, т. к. может пол-ся ур-е, в кот. все коэф-ты и b = 0.

В рез-те преобр-й дан. сист. м. б. след.о вида: 1.В ступенчатой СЛУ, равносильной данной, число уравн-й = числу неизв-х, тогда ступенчатая СЛУ, а значит и равносильная ей дан. сист., б.иметь 1 реш-е, т. е. они явл-ся определенными. 2. В ступенчатой СЛУ, равносильной дан., число уравн-й r меньше числа неизве-х n. В эт. случае СЛУ им. бесчисленное мн. реш., т. е. явл. неопределенной; где r главных неизв-х, n – r свободных неизв-х. 3. Ступенчатая СЛУ, равносильная данной, сод-т ур. вида 0x₁ + 0x₂ + 0х₃ +… + 0x_n = b_n , b_n ≠ 0. В этом случае СЛУ не имеет решений, т. е. явл. несовместной.

Пусть АMat_m,nR, a_ij R ; i=1,…,n; j=1,…,n;

О8:Строчечным или (столбцовым) рангом матр.наз. ранг ее сист. строк (столбцов). О9: Рангом матр. наз.ее строчечный или столбцовый ранг.

Теорема ( критерий совместности системы линейных уравнений или Кронекера-Капелли) СЛУ (1) совместна <=> rang A = r =rang Ā, где Ā – расширенная матр.СЛУ(1).