Вопрос 9.

Дифференцируемые ф-ции одной и нескольких действит. переменных.Производная и дифф-ал,частные производные и полный дифф-ал,их геометрический смысл. Пр-ла дифф-ия.

Пусть задана функция y=f(x) на пром. X, x₀ X. Придадим точке х₀ приращение ∆х, чтобы х₀+∆х X. Тогда y=f(x) получит приращение y=f(∆х)=f(х₀+∆х)-f(x₀).

О1. Производной функции f(x) в т. х₀ называется предел отношения приращения функции в этой точке к приращению аргумента при условии, что приращение аргумента стремится к 0.

О2. Если предел существует и конечен в т.х₀, то функция f(x) называется дифференцируемой в т. х₀.

О3. Функция f(x) называется дифференцируемой в т х, если ее приращение в этой точке ∆f(х) допускает представление ∆f(х)=A·∆х+α(∆х)· ∆х, где А не зависит от ∆х, α(∆х) – беск. мал. при ∆х→0, ( .

Т. Если функция f(x) дифференцируема в т. х, то она непрерывна в этой точке.(обратное неверно)

Д-во. По О2 сущ-ет конечный предел

След-но, f(x) непрерывна в т. х₀.

О4. Линейная функция А·∆х называется дифференциалом функции в т. х₀ (df(x₀)).

Правила дифференцирования.

1. Пусть функции u(x) и v(x) имеют производную в т. х. Тогда их сумма также имеет производную в этой точке, причем (u(x)±v(x))'=u'(x)±v'(x).

Д-во. Рассмотрим разностное отношение

2. Пусть функции u(x) и v(x) имеют производную в т. х. Тогда u(x)·v(x) имеет производную в этой точке, причем (u·v)'=u'v±uv'.

3. Пусть функции u(x) и v(x) имеют производную в т. х, и 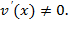Тогда их частное также имеет производную в этой точке, причем

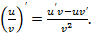
4. Пусть функция y=f(x) имеет производную в т. х. Тогда имеет производную в этой же точке функция c·f(x), c=const, причем

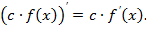
5. Если функции u₁(x), u₂(x), …, u_n(x) имеют производную в т. х, то имеет производную в этой же точке и линейная комбинация c₁u₁(x)+c₂u₂(x)+…+c_nu_n(x) причем

6. Дифференцирование сложных функций. Пусть функция y=f(x) имеет производную в т. х₀, а функция z=g(y) имеет производную в т. y₀=f(x₀). Тогда функция z=g(f(x)) имеет производную в т. х₀, причем

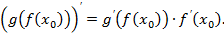
Д-во. Придадим переменной х приращение ∆х. Тогда y получит приращение ∆y. Заметим, что при ∆x→0, ∆y→0. Т.к. ф-ия z=g(y) имеет производную в т. y₀, то , где α(∆y)→0 при ∆y→0 – беск. мал. ф-ия. Разделим обе части на ∆х и перейдем к пределу

О5. Пусть ф-ция u=f(x,y,z) (1) определена в некоторой окрестности т. (x₀,y₀,z₀). Зафиксируем переменные y=y₀, z=z₀, получим ф-цию от одной переменной u=f(x,y₀,z₀) (2).Частной произвоной ф-ции (1) по переменной х в т. (x₀,y₀,z₀) наз-ся обычная производная ф-ции (2) в т.х₀.

Дифференциалы назовем частными дифференциалами по переменным x,y,z.

О6. Пусть ф-ция z=f(x,y) определена в некоторой δ-окрестности т.М₀(x₀,y₀). Возьмеме т. M(x,y) , ρ=ρ(M,M0)= <δ/

∆z=f(x₀+∆x,y₀+∆y)-f(x₀,y₀)-полное приращение ф-ции z=f(x,y) в т.(x₀,y₀).

Ф-ция z=f(x,y) наз-ся дифференцируемой в т.(x₀,y₀), если ее полное приращение ∆z допускает представление ∆z=A·∆x+B·∆y+α(∆x,∆y), где А,В-некоторые числа. α(∆x,∆y)=ε·ρ, ρ≠0, где lim ε=0 при ρ→0.

О7. Если ф-ция дифференцируема в т.(x₀,y₀), то линейная ф-ция dz=A dx+B dy относ-но переем. ∆x,∆y наз-ся полным дифф-лом ф-ции в т.(x₀,y₀).

Т. Если ф-ция z=f(x,y) дифф-ма в т.(x₀,y₀), то она непрерывна в этой точке.

Д-во. Т.к. ф-ция f(x,y) дифф-ма в т.(x₀,y₀), то ее приращение допускает представление ∆z=ε₁∆x+ε₂∆y+A∆x+B∆y.

Т.к. ,то при ρ→0 ∆z→0, (lim ∆z=0),т.е. ф-ция z=f(x,y) непр-на в т.(x₀,y₀).

Т. Если ф-ция z=f(x,y) дифф-ма в т.(x₀,y₀), а dz=Adx+Bdy-ее дифф-ал в т.(x₀,y₀), то в т.(x₀,y₀) сущ-ют частные производные Т.о.

Геометрический смысл. Пусть функция f(x) определена на интервале (a; b) и непрерывна в т. х₀ (a; b). х₀+∆х (a; b). Обозн. через M₀ (x₀; f(x₀)), M(x₀+∆x; f(x₀)+∆x). Заставим М стремится к М₀. Секущая ММ₀ будет стремиться занять положение положит. направл. оси Ох.

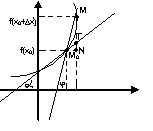
Геом. смысл производной: производная ф-ции в т. х₀ равна угловому коэффициенту касательной, проведенной к графику ф-ции в точке с абсциссой х₀.

y-y₀=k(x-x₀) – ур-е прямой, проход. через точку (x₀;y₀), k-угловой коэф-т.

y₀=f(x₀), ,

Ур-ие касат. y-f(x₀)=f '(x₀)(x-x₀)

y=f(x₀)≠f '(x₀)(x-x₀)

Из ∆MM₀N: MN=M₀N·tg , TN=M₀N·tg α=f '(x₀)·∆x=df(x₀).

Геом. смысл дифференциала: дифф-ал ф-ции в точке равен приращению ординаты касательной, проведенной к графику ф-ции в точке с абсциссой х₀, если соотв-щее приращение абсциссы равно ∆х. Геом. смысл полного дифференциала: полный дифференциал ф-ции в т.(x₀,y₀) равен приращению аппликаты z касательной плоскости к графику ф-ции z=f(x,y) в т.(x₀,y₀,f (x₀,y₀)).

Вопрос 10. Основные теоремы дифференциального исчисления. Условия постоянства, монотонности и выпуклости числовой функции на промежутке. Экстремумы и точки перегиба функции одной переменной. Экстремумы функций нескольких переменных.